Презентація "Функції, їхні властивості, графіки. (повторення)"

Функції, їхні властивості, графіки. (повторення)Підготовлнно: Вчитель І категорії, Тухватулліною С. А. АЛГЕБРА. 10 КЛАС. Урок №2.2024-2025

Повторення, систематизація та узагальнення знань, умінь і навичок учнів по темі «Функції» та «Числові послідовності»; розвивати вміння працювати разом, творчо і логічно мислити; працювати кожному і навчити іншого; робити висновки; узагальнювати факти; сприяти моральному вихованню учнів у ході уроку. Тип: повторення, систематизації знань, умінь, навичок . Обладнання: підручник, відеоуроки, онлайн тест, таблиці. Мета уроку:

План уроку 1. Організаційний момент 2. Перевірка домашнього завдання 3. Повторення, систематизація та узагальнення знань учнів з теми «Функція» 4. Повторення, систематизація та узагальнення умінь і навичок учнів з теми «Числові послідовності» 5. Підсумок уроку 6. Домашнє завдання

Любі учні, добрий день! Зичу праці і старання! А ще, друзі, всім бажаю Справдити всі сподівання! 1. Організаційний момент

2. Перевірка домашнього завдання Що називається лінійним рівнянням з двома змінними ?. Назви основні властивості числових нерівностей. Лінійною нерівністю називається нерівність, яка…. Системою двох рівнянь з двома змінними називають…Яку систему називають лінійною?Назви способи розв’язування системи рівнянь. Рівняння виду ax + by = c , де a, b, c — числа (коефіцієнти), x та y - змінні, називається лінійним рівнянням з двома змінними .1. Якщо a>b і b>c, тоді a>c. ; 2. Якщо a > b, тоді a + c > b + c; Якщо a > b і k > 0, тоді ak > bk; 4. Якщо a > b і k < 0, тоді ak < bk. Лінійною нерівністю називається нерівність, яка дана або перетворена до форми ax>b або ax

3. Повторення, систематизація та узагальнення знань учнів з теми «Функція» Означення функції. Аргумент функції, область визначення функції, область значень функції. Способи задання функції. Найбільше і найменше значення функціїЛінійна функція. Графік лінійної функції. Зростаючі та спадні функції Парні і непарні функції, розміщення графіків цих функцій. Означення і властивості квадратичної функції Перетворення графіків функцій

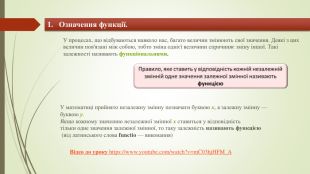
Означення функції. У процесах, що відбуваються навколо нас, багато величин змінюють свої значення. Деякі з цих величин пов'язані між собою, тобто зміна однієї величини спричиняє зміну іншої. Такі залежності називають функціональними. У математиці прийнято незалежну змінну позначати буквою х, а залежну змінну — буквою у. Якщо кожному значенню незалежної змінної х ставиться у відповідність тільки одне значення залежної змінної, то таку залежність називають функцією (від латинського слова functio — виконання)Відео до уроку https://www.youtube.com/watch?v=m. C03hj. HFM_A

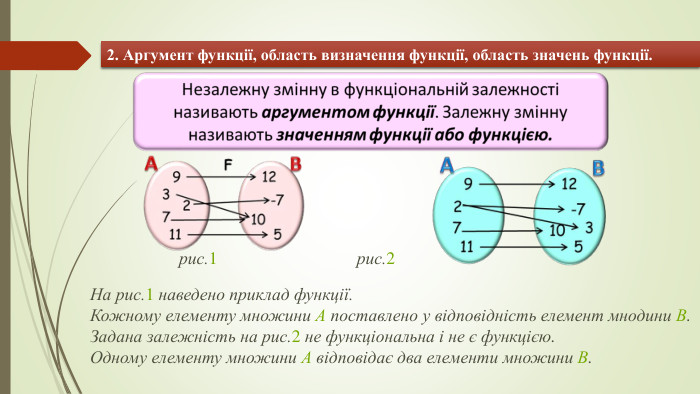
2. Аргумент функції, область визначення функції, область значень функції. На рис.1 наведено приклад функції. Кожному елементу множини А поставлено у відповідність елемент мнодини В. Задана залежність на рис.2 не функціональна і не є функцією. Одному елементу множини А відповідає два елементи множини В. рис.1рис.2

Функцію вважають заданою, якщо вказано її область визначення та правило, за допомогою якого можна за кожним значенням незалежної змінної знайти значення залежної змінної.t час 5101520 T °C102030401. Катер пли по озеру t годин зі швидкістю 45 км/год і пройшов S км. t год — аргумент функції S км — значення функції 2.  y=2x2−5x x — аргумент функції y — значення функції 3. Зміна температури води від часу нагрівання задана в таблиці t  — аргумент функціїT — значення функціїПРИКЛАДИ

3. Способи задання функції. Функцію вважають заданою, якщо вказано її область визначення та правило, за допомогою якого можна за кожним значенням незалежної змінної знайти значення залежної змінної. В математиці розклядаю чотири способи задання функціїВідео до уроку https://www.youtube.com/watch?v=x1 Rvrafy. Nck&embeds_referring_euri=https%3 A%2 F%2 Fwww.miyklas.com.ua%2 F&source_ve_path=OTY3 MTQ

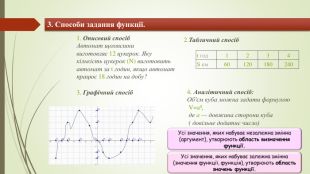
3. Способи задання функції. 1. Описовий спосіб. Автомат щохвилини виготовляє 12 цукерок. Яку кількість цукерок (N) виготовить автомат за t годин, якщо автомат працює 18 годин на добу? 2. Табличний спосібt год1234 S км601201802403. Графічний спосіб 4. Аналітичний спосіб: Об'єм куба можна задати формулою V=a³, де а — довжина сторони куба ( довільне додатнє число)

3. Способи задання функції. 1.  y = 3x³−7x. Незалежна зміння x і залежна змінна y можуть приймати довільні значення. Область визначеня функції будь—яке число і область значення функції будь—яке число. 2.  y = 2x + 8/x−3 Функція представлена дробом 2x+8x−3. Даний дріб має зміст якщо x≠3. Область визначення x≠3. Область значень такої функції ти навчишся знаходити пізніше. 3. Функція задана табличноx2359y12−5932 Область визначення: 2; 3; 5; 9 Область значення: 12; −5; 9; 32 ПРИКЛАДИ:

4. Найбільше і найменше значення функції. Нулі функції. Характеризуючи властивості функції, часто відмічають також, у яких точках вона набуває найбільшого значення, а в яких найменшого. Визначити найбільше або найменше значення функції можна тільки на заданому проміжку області визначення, знайшовши всі значення функції на цьому проміжку. Ще однією важливою характеристикою є нулі функціїКорені цього рівняння є нулями функції. Якщо функція задана таблично, потрібно серед значень функції відшукати нульове. Аргумент цього значення і буде нулем функції. Щоб знайти нулі функції y=f(x), потрібно розв’язати рівняння f(x)=0. ПРИКЛАД: Знайди нулі функції1.y=4x−12y=0⇒4x−12=04x=12x=3 Відповідь: x=3 нуль функції

5. Лінійна функція. Зростаючі та спадні функції . Лінійна функція — це функція, яку можна задати формулоюy=kx+b, де x — незалежна змінна, k і b — деякі числа. Графіком лінійної функції y=kx+b є пряма. Щоб побудувати графік даної функції, нам достатньо мати координати двох точок, що належать графіку функції. Побудуємо на координатній площині x. Oy точки (0;−2) і (4;0), оформлені у таблиці, і проведемо через них пряму. У ході побудови графіків лінійних функцій, можна ніби «підніматися вгору» або «спускатися з гірки», тобто лінійна функція або зростає, або спадає. Якщо k>0, тоді лінійна функція y=kx+b зростає;якщо k<0, тоді лінійна функція y=kx+b спадає. Відео до уроку https://www.youtube.com/watch?v=eo. NIWe. C8 PDQ&embeds_referring_euri=https%3 A%2 F%2 Fwww.miyklas.com.ua%2 F&source_ve_path=OTY3 MTQ

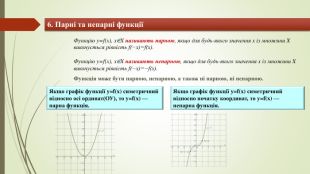
6. Парні та непарні функціїФункцію y=f(x), x∈X називають парною, якщо для будь-якого значення x із множини X виконується рівність f(−x)=f(x). Функцію y=f(x), x∈X називають непарною, якщо для будь-якого значення x із множини X виконується рівність f(−x)=−f(x). Функція може бути парною, непарною, а також ні парною, ні непарною. Якщо графік функції y=f(x) симетричний відносно осі ординат(ОУ), то y=f(x) — парна функція. Якщо графік функції y=f(x) симетричний відносно початку координат, то y=f(x) — непарна функція.

7. Означення і властивості квадратичної функції Квадратичною називають функцію виду у = ах² + bх + с; де а, b, с — дійсні числа, а ≠ 0. Приклади квадратичних функцій: у = 2х² + 3х – 1, у = х² + 3х, у = 4х² , у = −2х² , у = х² .1. Зростання і спадання квадратичної функції при k>0 Побудуємо графік функції y=x² і дослідимо її на монотонність.x−2−1012y41014  Функція зростає на проміжку [0;+∞) і спадає на проміжку (−∞;0].2. Зростання і спадання квадратичної функції при k<0 Побудуємо графік функціїy=−x2 і дослідимо її на монотонність. Графік даної функції можна отримати відобразивши симетрично графік функції y=x2 щодо осі x або побудувати по точках.x−2−1012y−4−10−1−4 Функція зростає на проміжку (−∞;0] і спадає на проміжку [0;+∞).

ТАБЛИЦІ ДЛЯ КОРИСТУВАННЯ

ДОМАШНЯ РОБОТАВИКОНАТИ ТЕСТ: Властивості функцій. Лінійна функція https://naurok.com.ua/test/vlastivosti-funkci-2953690.html. Перегляннути відео до уроку . Означення функції. https://www.youtube.com/watch?v=m. C03hj. HFM_Aь2. Способи задання функції https://www.youtube.com/watch?v=x1 Rvrafy. Nck&embeds_referring_euri=https%3 A%2 F%2 Fwww.miyklas.com.ua%2 F&source_ve_path=OTY3 MTQ 3. Лінійні функції https://www.youtube.com/watch?v=eo. NIWe. C8 PDQ&embeds_referring_euri=https%3 A%2 F%2 Fwww.miyklas.com.ua%2 F&source_ve_path=OTY3 MTQ Опрацювати презентацію до уроку.

Рефлексія. Вправа «Допитлива квіточка» Над чим ще потрібно подумати?Який у тебенастрій?Які завданнялегше буловиконувати?Що сподобалося?Корисний був урок?