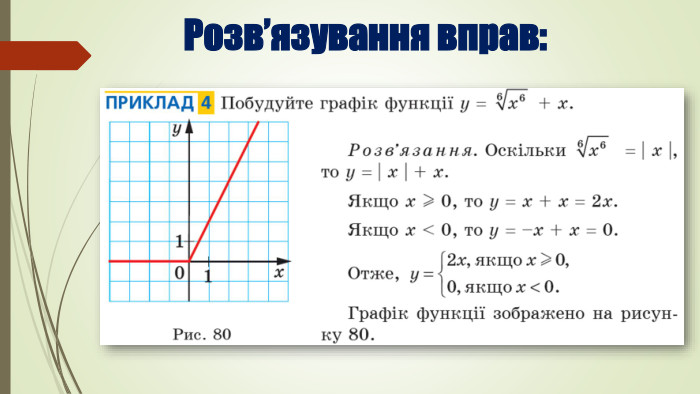
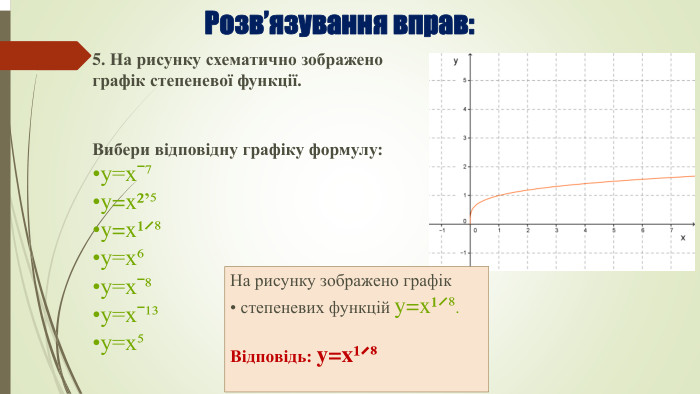
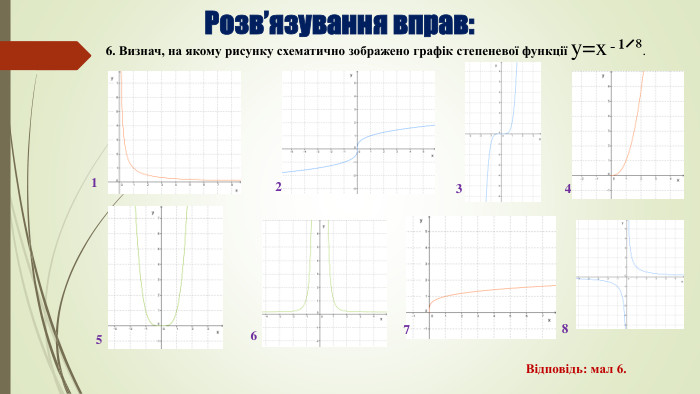
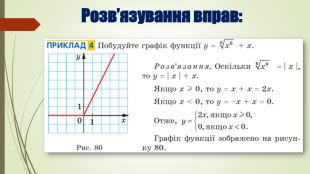
Розв’язування вправ. Властивості арифметичного кореня n-го степеня. Степеневі функції, їх властивості та графіки.

Розв’язування вправ. Властивості арифметичного кореня n-го степеня. Степеневі функції, їх властивості та графіки. Математика 10 клас. Підготувала: Вчитель фізики та математики, С. Тухватулліна. Урок створеня для удосконалення навичок учнів з даної теми

Мета уроку: повторити й систематизувати знання учнів про властивості арифметичного кореня n-го степеня, степеневі функції, їх властивості та графіки; сформувати знання про властивості кореня n – го степеня, степеневі функції; формувати вміння застосовувати ці знання під час перетворення виразів;формувати інформаційну та полікультурну компетентність;сприяти формуванню та розвитку інтелектуальних та творчих здібностей учнів;розвивати логічне мислення, математичну мову, пізнавальний інтерес учнів, вміння шукати цікаву інформацію;виховувати відповідальність, прагнення до самовдосконалення, патріотизм, любов до рідного краю. Компетенції: Спілкування державною мовою: розуміти, пояснювати і перетворювати тексти математичних задач (усно і письмово), грамотно висловлюватися рідною мовою; доречно та коректно вживати в мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку, аргументувати, доводити правильність тверджень; поповнювати свій словниковий запас. Тип уроку: систематизація знань. Обладнання: робочий зошит, підручник, комп’ютерна презентація; інтерактивні завдання в додатку Learning Apps

Перевірка домашнього завдання: Кубічним коренем із невід'ємного числа a називають… Кубічним коренем із невід'ємного числа a називають таке невід'ємне число, куб якого дорівнює a. Інакше кажучи, рівність ³√a =b означає, що b³=a.³√27=³√27=3, бо3³=27³√1=1, бо1³=1³√1=³√0=0, бо0³=0³√0=³√64=³√64=4, бо4³=64𝟐𝒌+𝟏𝒂𝟐𝒌+𝟏= 𝒂 𝟐𝒌𝒂𝟐𝒌= 𝒂 𝒏𝒂𝒃= 𝒏𝒂∙𝒏𝒃 𝒏𝒂𝒃= 𝒏𝒂𝒏𝒃  𝒏𝒂𝒌= 𝒏𝒂𝒌 𝒏𝒌𝒂= 𝒏𝒌𝒂 𝒏𝒌𝒂𝒌= 𝒏𝒂 

Розв’язування вправ:

Розв’язування вправ:

Розв’язування вправ:

5. На рисунку схематично зображено графік степеневої функції.   Вибери відповідну графіку формулу:y=xˉ⁷y=x²՚⁵y=x¹⸍⁸y=x⁶y=xˉ⁸y=xˉ¹³y=x⁵На рисунку зображено графік степеневих функцій y=x¹⸍⁸. Відповідь: y=x¹⸍⁸Розв’язування вправ:

6. Визнач, на якому рисунку схематично зображено графік степеневої функції y=x ˉ ¹⸍⁸.12345678 Відповідь: мал 6. Розв’язування вправ:

7. Відомо, що f(x)=x⁵⸍². f(0,01) = ? 4. На рисунку зображено графіки степеневих функцій, формула яких має вигляд y=xⁿ. Назви, яке n, якщо n∈Z. Відповідь: 1.від'ємне непарне число 2. від'ємне парне число3.додатне парне число 4. додатне непарне число У функції якого кольору показник за модулем (не рахуючи знака) менший?у зеленої у червоноїВідповідь: (2) показник n — від'ємне парне число, показник за модулем менший у зеленої функції. Кроки розв'язання:f(x)=x ⁵⸍²Щоб знайти f(0,01), необхідно підставити замість x значення, що дорівнює 0,01.f(0,01)=0,01 ⁵⸍² =(0,1²) ⁵⸍² =0,1² ̽ ⁵⸍² =0,1⁵=0,00001 Розв’язування вправ:

8. Побудуй графік функції y=𝟒х − 3, використовуючи допоміжну систему координат. Порівняй побудований графік із даними в кроках розв'язання. Додаткові запитання1. Якою є дана функція?Відповідь: зростаючамонотоннавід'ємна 3. У напрямку якої осі переміститься графік?Відповідь:осі Oxосі Oyне переміститься. Розв’язок:y=𝟒х − 3 — функція спадає на всій області визначення, функція монотонна. Функція не визначена, якщо x=0. Основна функція y=𝟒х , графіком якої є гіпербола. Таблиця значень  x−8−4−2−11248 y−12−1−2−442112  Графік функції y=𝟒х − переміститься на 3 одиниці вниз. Проводимо допоміжну вісь x′ через точку (0;−3). У допоміжній системі координат будуємо графік функції y=𝟒х  Функція називається спадною на проміжку (a;b), якщо для будь-яких двох точок x1,x2 цього інтервалу, таких, що x1f(x2), або функція називається спадною, якщо більшому значенню аргументу відповідає менше значення функції. Постійна функція не збільшується і не зменшується. Постійною функцією є y=a. Наприклад, функція y=3, графік якої паралельний осі Ox. Зростаючі і спадні функції називаються монотонними. Наприклад, монотонною функцією на всій області визначення є лінійна функція, показникова функція, логарифмічна функція, функція квадратного кореня, обернена пропорційність (дана функція).2. За яких значень аргументу функція не визначена?Відповідь:x>0x=3x=04. У якому напрямку переміститься графік?Відповідь:вправовлівовнизне переміститьсявгору. Відповіді: 1)монотонна; 2) x=0; 3) по осі Оу; 4) 4) вниз. Розв’язування вправ:

Пропоную вам пограти та закріпити свої знання: Степеневі функції:https://learningapps.org/17279136 ПОЛЕ ЧУДЕС:https://learningapps.org/view20982179 Домашнє завдання: