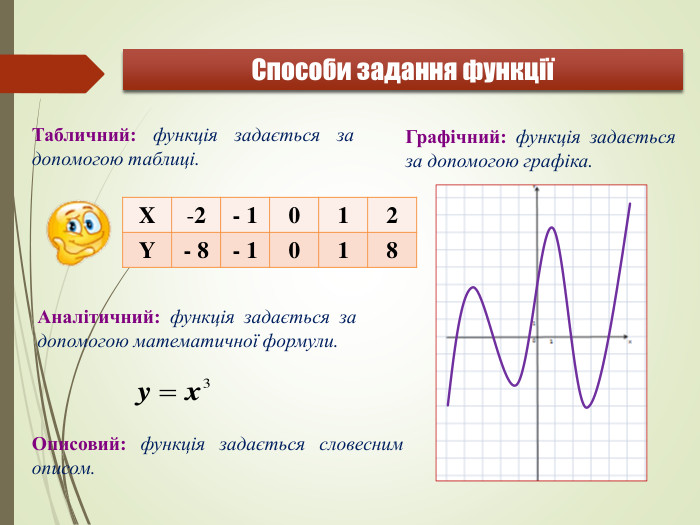
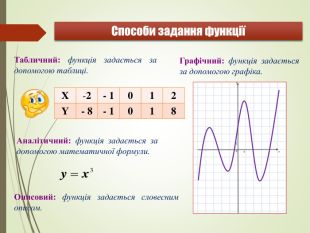
Презентація "ФУНКЦІЇ, ЇХНІ ВЛАСТИВОСТІ. Узагальнення і систематизація знань. "
Про матеріал
Узагальнити та систематизувати знання із теми «Функції, їх властивості та графіки» Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку