Презентація "Геометрична прогресія в нашому житті"

Геометрична прогресія в нашому життіПідготувала вчителька математики Бузівської гімназії Личківського ліцею Трясак Любов Олексіївна

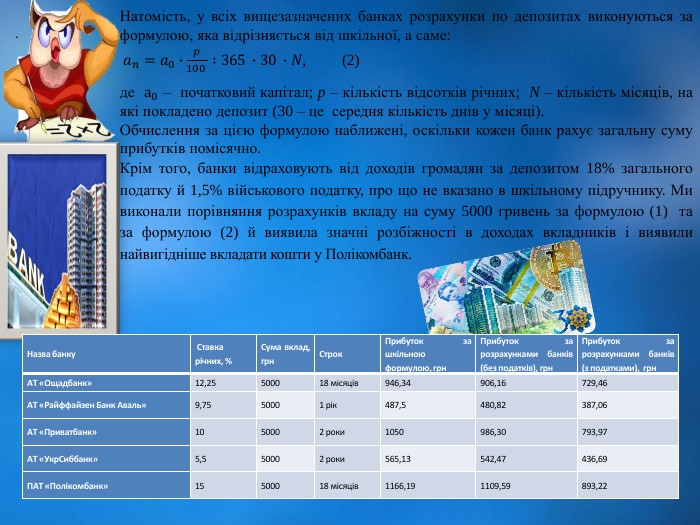
Геометричною прогресією називається послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число. Стале число- множник називається знаменником геометричної прогресії і позначається літерою q.    Члени прогресії позначаються як bn, де під індикатором n мається на увазі порядковий номер члена у прогресії.      Передбачається, що ані перший член, ані знаменник геометричної прогресії не дорівнюють нулю.    ФОРМУЛИ ТА ВЛАСТИВОСТІ ГЕОМЕТРИЧНОЇ ПРОГРЕСІЇq=𝑏𝑛+1𝑏𝑛 S= 𝑏11−𝑞 

1. Задачі на знаходження членів геометричної прогресії, використовуючи формулу n-го члена і властивості геометричної прогресії 1)Знайти знаменник і третій член геометричної прогресії (bn): 1; 1,5; … . 2)Довести, що послідовність 8; -4; 2; -1; є геометричною прогресією.3)Знайти знаменник геометричної прогресії (bn), у якій b7 = -12, b9 = -108 . Розв‘язок. Використавши формулу n- го члена геометричної прогресії, одержимо:b9 = b1q8 = -108, b7 = b1q6 = -12. Звідси: q 2 = 9; q = -3 або q = 3. 2. Задачі на відшукання суми n перших членів геометричної прогресії 1)Знайти суму восьми перших членів геометричної прогресії (bn): 3; -6; 12 2)Знайти перший член геометричної прогресії (bn), якщо четвертий її член утричі більший від третього, а сума перших п'яти членів дорівнює -12,1. Розв’язок. Оскільки b4 = 3b3, то q = 3. За умовою S5 = -12,1, тому: b1+3b1+9b1+27b1+81b1=-12,1, -12,1 = b1(1+3+9+27+81); -12,1 = 121 · b1; b1 = -0,1.

3. Задачі на відшукання суми нескінченої геометричної прогресії1)Знайти суму нескінченної геометричної прогресії (bn): 6; -2; … . 2) Знайдіть перший член нескінченної геометричної прогресії,у якій q = -  14, S = 50. 3)Запишіть число 0,(7) у вигляді звичайного дробу. 4) Перетворити періодичний дріб у звичайний дріб: 0,3(7) Розв’язок. Маємо мішаний періодичний дріб 0,3 7 =0,3777… 310 7100  71000 710000  … Після першого доданка маємо нескінченно спадну геометричну прогресію з першим членом b1  7100 та знаменником q  110. Тому 0,37  = 310+ 7/1001−1/10 =310 + 7100 : 910 = 310   + 790 = 27+790 = 3490 = 1745 . 

. Застосування прогресії1. Геометрична прогресія в токарному цеху. У 1876 р. академік А. В. Гадолін на підставі точних математичних розрахунків довів, що верстати слід будувати зі ступенями швидкостей, які утворюють геометричну прогресію.2. Геометрична прогресія в машинобудуванніЗа законом геометричної прогресії побудовано розмірність металорізальних верстатів та інструментів, встановлено нормальні діаметри і довжини в машинобудуванні. Тому геометрична прогресія становить математичну основу стандартизації різноманітної промислової продукції.

. Геометрична прогресія в будівельній справі. В архітектурі, будівельній справі використовуються колони. Вони мають форму не циліндра, а зрізаного конуса. Сила тиску в горизонтальних шарах колони зростає у напрямку до нижньої основи. Для збереження рівномірності від тиску довжини колони потрібно збільшувати площі її поперечних перерізів. Площі поперечних перерізів, рівновіддалених один від одного, становлять геометричну прогресію.

. Ми дослідили утворення фінансових пірамід та яку вигоду мають організатори. Мені розповіла бабуся , що в 2002 році вона одержала листа , в якому пропонували внести зазначену плату за вказаними адресами по 1 грн., а потім заплатити ще по 5 таким же адресами, викресливши першу адресу і дописавши свій останнім, то через деякий час ви отримаєте купу грошей. Вона виконала всі умови, але грошей не отримала. В чому ж справа ?.  Розв’язок. Справа в тому, що число учасників збільшується у 5 разів з кожним колом. Якщо п'ятірка організаторів підпише, припустимо, 120 людина зі своїми адресами, то в першому колі беруть участь 120 чоловік, у другому - 600 , у третьому - 3000 , ... , в десятому - 234375000 чоловік. Так що учасник, що включився у восьмому чи дев'ятому колі, вже нічого не отримає. Що й сталося з моєю бабусею…

. В Україні не припиняється падіння економіки через кризу та пандемію. Однак інфляція залишається низькою, а ставки депозитів у банках навіть дешевшають. Якщо людина успішно планує бюджет і заощаджує кошти, то існує спосіб їх ще й примножити. Для цього їй необхідно покласти гроші у стабільний банк на депозит під відсотки. Шкільний підручник з алгебри для 9 класу пропонує задачі прикладного змісту, які часто доводиться розв’язувати банківським працівникам. Для цього пропонується формула складних відсотків:𝑎𝑛=𝑎01+𝑝100𝑛  а0– початковий капітал; p – кількість відсотків річних; n – кількість років, на які покладено депозит. Ми дізналися, що у місті Новомосковську на даний час діє 5 банків: АТ «Ощадбанк» ПАТ «Полікомбанк»АТ «Укр. Сиббанк»АТ «Райффайзен Банк Аваль»АТ «Приватбанк»Ми відвідали ці відділення банків і дізнались про умови вкладів по депозитах та правила їх виплат. У кожного банку визначений максимальний термін вкладу – від одного до двох років та різні відсотки виплат. .  

. Натомість, у всіх вищезазначених банках розрахунки по депозитах виконуються за формулою, яка відрізняється від шкільної, а саме: 𝑎𝑛=𝑎0∙𝑝100  :365 ∙30 ∙𝑁, (2)де а0 – початковий капітал; p – кількість відсотків річних; N – кількість місяців, на які покладено депозит (30 – це середня кількість днів у місяці). Обчислення за цією формулою наближені, оскільки кожен банк рахує загальну суму прибутків помісячно. Крім того, банки відраховують від доходів громадян за депозитом 18% загального податку й 1,5% військового податку, про що не вказано в шкільному підручнику. Ми виконали порівняння розрахунків вкладу на суму 5000 гривень за формулою (1) та за формулою (2) й виявила значні розбіжності в доходах вкладників і виявили найвигідніше вкладати кошти у Полікомбанк.  {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Назва банку Ставка річних, %Сума вклад, грн. Строк. Прибуток за шкільною формулою, грн. Прибуток за розрахунками банків (без податків), грн. Прибуток за розрахунками банків (з податками), грн. АТ «Ощадбанк»12,25500018 місяців946,34906,16729,46 АТ «Райффайзен Банк Аваль»9,7550001 рік487,5480,82387,06 АТ «Приватбанк»1050002 роки 1050986,30793,97 АТ «Укр. Сиббанк»5,550002 роки 565,13542,47436,69 ПАТ «Полікомбанк»15500018 місяців1166,191109,59893,22

. Інші прояви прогресії у навколишньому світіВ наш час актуальною стає проблема захворювання суспільства різноманітними хворобами , зокрема вірусом Ковід-19. Бактерії розмножуються за законом геометричної прогресії. Бактерія, потрапивши в організм, до кінця 20-ї хвилини ділиться на дві, кожна з них до кінця 20-ї хвилини знов ділиться на дві і т.д. Скільки бактерій стане в організмі через добу Розв’язання 1доба=24год.; 24год.=1440хв.; 1440:20=72 За умовою задачі отримаємо геометричну прогресію: 1;2;4;8;…; b1=1, q=2 Sn=((b1(qn-1)):q-1)=((1*(272 -1)):1)= 272 -1= 272(бактерії). В організмі за добу буде 272 бактерій. Дослідження показало, яке значення медичних заходів світової спільноти щодо попередження розповсюдження катастрофічних наслідків цього вірусу. Фармакологія. Купуючи в аптеці для мами ліки від тиску, ми звернули увагу на те, що дози діючих речовин ліків « Берліпріл», «Енап», «Каптопріл», «Лізінопріл», «Раміпріл» складають геометричну прогресію, де знаменник q =2.

. ЗНО рівень 2. 1. У геометричній професії 𝑏4=3; 𝑏17=14,7. Обчислити 𝑏9*𝑏12. Розв'язання: Враховуючи властивості геометричної прогресії,запишемо її 𝑏9 через 𝑏4 та 𝑏12 через 𝑏17. 𝑏9= 𝑏4*𝑞5,𝑏17 =𝑏12*𝑞5звідси 𝑏12=𝑏17𝑞5. Бачимо, що при множенні знаменник геометричної прогресії спрощується 𝑏9∗𝑏12=𝑏4*𝑞5 *𝑏17𝑞5=𝑏4*𝑏17= 3*14,7= 44,1 ЗНО підвищений рівень.1. У геометричній прогресії b10* b14* b21=-0,125. Обчислити b15. Розв'язання. Знайдемо суму індексів членів прогресії.10+14+21=45. Число 45 націло ділиться на 15 і в результаті ділення отримуємо 3. Отже заданий добуток не що інше, якb10*b14*b21=(b15)3 Звідси обчислюємо потрібний член прогресії𝑏15= 3𝑏21𝑏14𝑏10=3−0,125= - 0,5. 

Прогресу без прогресій не буває!