Урок "Властивості функцій"

Тема: Властивості функції

Мета: продовжувати вивчати властивості функцій, формувати поняття нулів функції; зростаючої та спадної функції та проміжків зростання та спадання функції; проміжків знакосталості функції; розвиток уяви, уваги; виховувати культуру математичного мовлення

Хід уроку

1.               Організаційний момент

Доброго дня! Я вітаю Вас на уроці алгебри. Мета якого  продовжити вивчати властивості функцій;  нулів функції; формувати поняття зростаючої та спадної функції та проміжків зростання та спадання; проміжків знакосталості функції; розвиток уваги, уяви.   Епіграфом до якого будуть слова Рене Декарта:

«Для того, щоб вдосконалити розум, треба більше роздумувати, ніж заучувати!»

2. Перевірка домашнього завдання
3. Актуалізація опорних знань

Усний рахунок (завдання зі збірників ДПА попередніх років).

Слайди 1-4

4. Сприйняття й усвідомлення нового матеріалу

Для того щоб досліджувати процеси і явища навколишнього світу, слід спочатку навчитися встановлювати характерні особливості відповідних математичних моделей. Передусім це стосується функцій.
Часто про властивості об’єкта можна робити висновки за його зображенням: фотографією, рентгенівським знімком, рисунком тощо.

«Зображенням» функції може слугувати її графік. Покажемо, як графік функції дає змогу визначити певні її властивості.

Схема дослідження функції.

1. Назва функції.

2. Область визначення.

3. Область значень.

4. Парність.

5. Нулі функції. Точки перетину з віссю ОУ.

6. Проміжки знакосталості функції.

7. Проміжки зростання та спадання функції.

8. Найбільше та найменше значення функції.

ь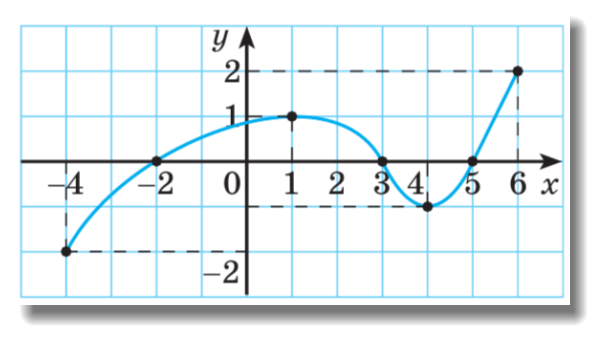

Нулі функції. (Слайд 6)

Розглянемо   функцію  y = f(x), графік якої зображено на малюнку. При х= -2, х=3, х=5 значення функції дорівнює нулю.

Зрозуміло, що нулі функції є абсцисами точок перетину графіка функції з віссю абсцис, а ординати цих точок дорівнюють нулю, адже точки належать осі абсцис.

Тому, щоб знайти нулі функції у = f(x), треба розв’язати рівняння f(х) = 0.
Проміжки знакосталості функції. (Слайд 7)

Функція y = f(x), графік якої зображено на малюнку, має додатні, нульові й від’ємні значення. На проміжку (–2; 3) її значення додатні. Це проміжок сталого знака: усі значення функції на цьому проміжку мають сталий знак «+». І проміжок (5; 6] є також проміжком сталого знака «плюс». Проміжки (–4; –2) і (3; 5) теж є проміжками сталого знака: усі значення розглядуваної функції y = f(x) на цих проміжках від’ємні.Чи обов’язково потрібно будувати графік функції у = f(x) для знаходження проміжків її знакосталості? Ні. Якщо функцію задано формулою, то проміжки знакосталості можна знайти, розв’язавши відповідні нерівності: f(x) > 0 або f(x) < 0.

Проміжки зростання та спадання функції (Слайди 8-10)

5. Перевірочна робота.
6. Закріплення вивченого матеріалу

Робота з підручником. № 8.7, 8.9

7. Підсумок уроку

8.Домашнє завдання п.8, №8.8, 8.10