Презентація.Геометричні фігури. Точки і прямі. 7 клас
Про матеріал
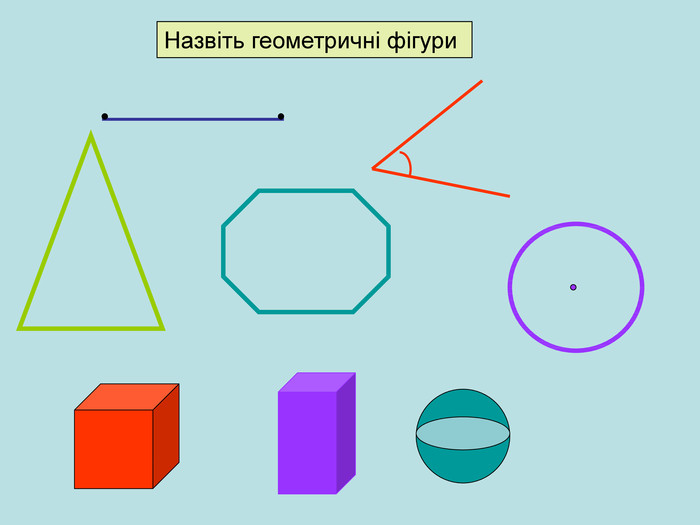
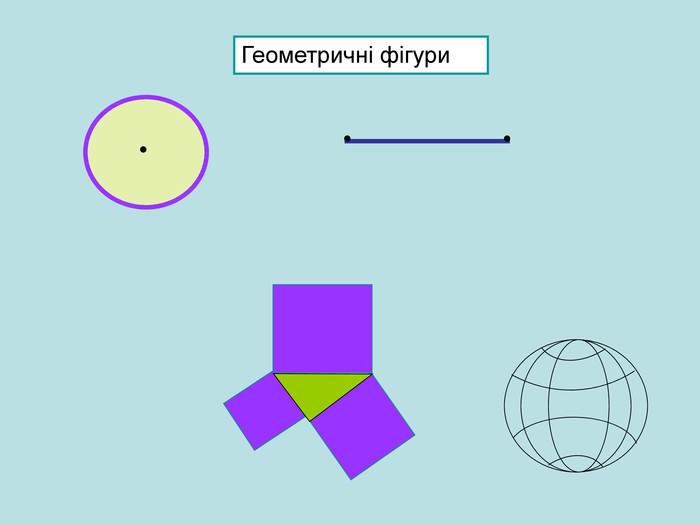
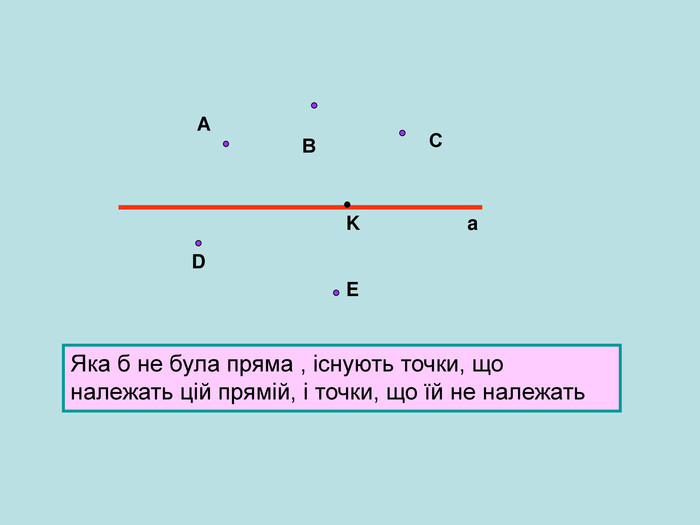
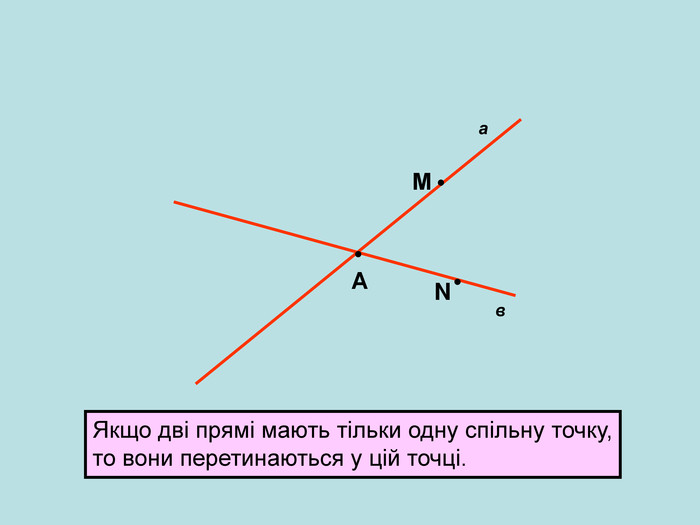
Презентація.Геометричні фігури. Точки і прямі. 7 клас
--------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------
Перегляд файлу
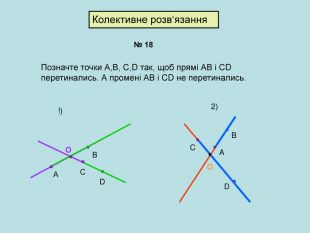
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Геометрія.(підручник) 7 клас (Тадеєв В.О.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку




















-

Катрін Альона Анатоліївна
06.09.2023 в 21:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Подолів Влад
05.09.2023 в 17:18
Загальна:
3.7
Структурованість
3.0
Оригінальність викладу
3.0
Відповідність темі
5.0
-

Yeskina Viktoriya
08.09.2022 в 19:06
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кравченко Аліна
05.09.2022 в 23:06
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Рябуха Наталія
31.08.2022 в 19:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-
Білецька Анастасія Володимирівна
04.09.2018 в 20:26
Дякую за корисну і цікаву презентацію!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 3 відгука