Презентація "Геометричний зміст визначеного інтеграла. Обчислення площ плоских фігур"
Про матеріал
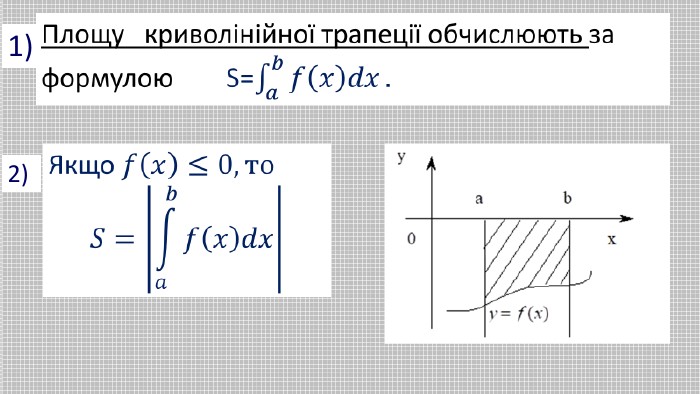
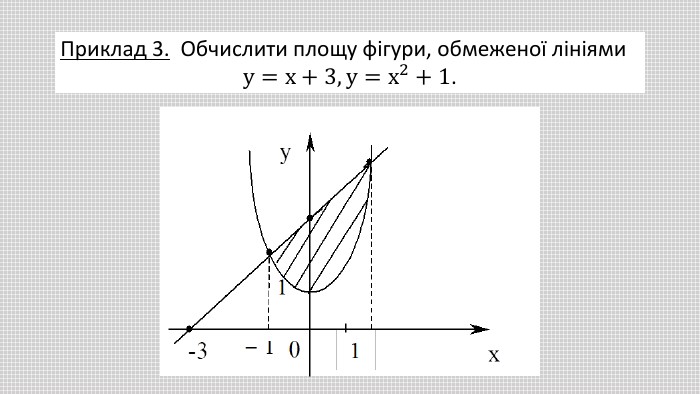
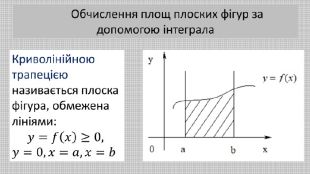
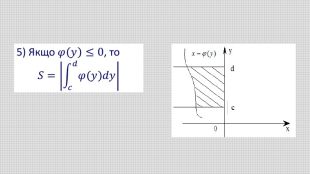
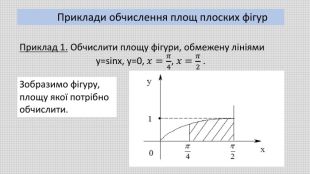
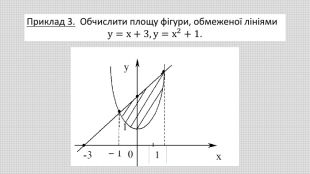
В презентації розглянуто геометричний зміст визначеного інтеграла та його застосування для обчислення площ плоских фігур. Наведено приклади різних плоских фігур і формули для обчислення їх площ. Обчислено площі конкретних плоских фігур. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


![Геометричний зміст визначеного інтеграла. З геометричної точки зору 𝑎𝑏𝑓𝑥𝑑𝑥 дорівнює площі криволінійної трапеції, що обмежена лініями x=a, x=b, відрізком [a; b] та графіком неперервної й невід’ємної на цьому відрізку функції y=f(x). Геометричний зміст визначеного інтеграла. З геометричної точки зору 𝑎𝑏𝑓𝑥𝑑𝑥 дорівнює площі криволінійної трапеції, що обмежена лініями x=a, x=b, відрізком [a; b] та графіком неперервної й невід’ємної на цьому відрізку функції y=f(x).](/uploads/files/2624350/353087/406796_images/2.jpg)