Презентація. Геометрія 7 клас. "Зовнішній кут трикутника"
Про матеріал
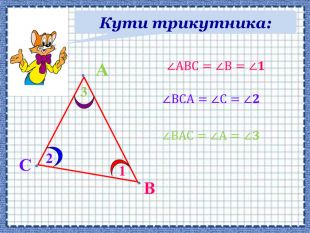
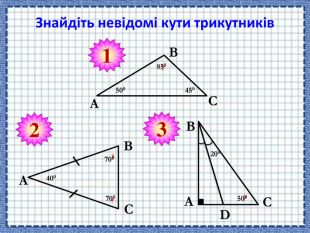
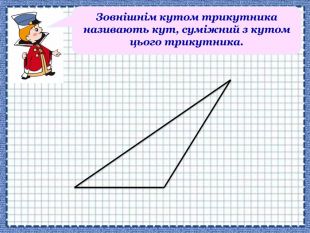
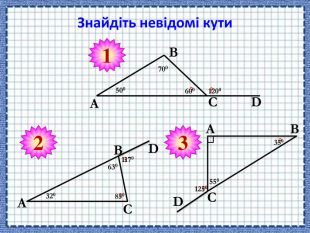
Сформувати поняття про зовнішній кут трикутника, його властивості; навчити застосовувати властивості зовнішнього кута трикутника й теорему про суму кутів трикутника під час розв'язування задач Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку





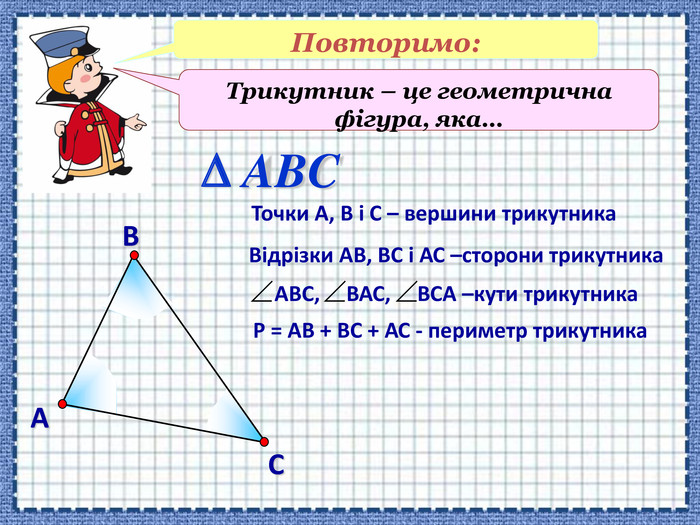
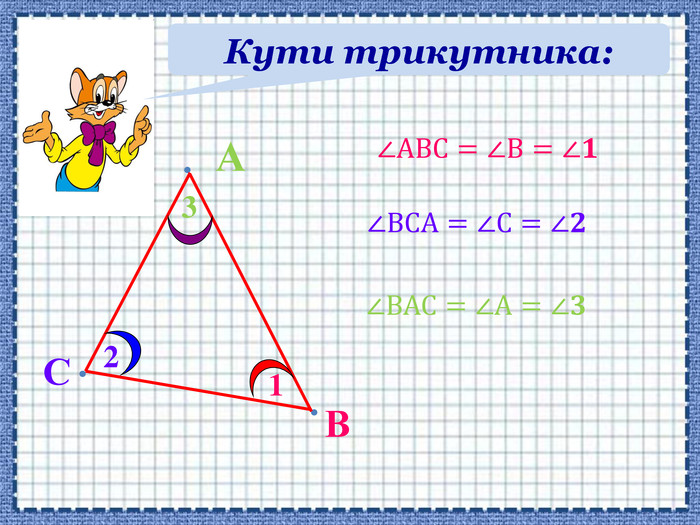

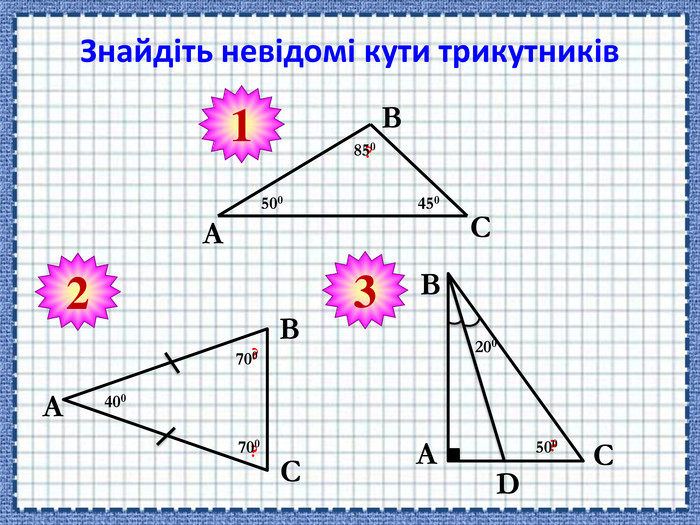
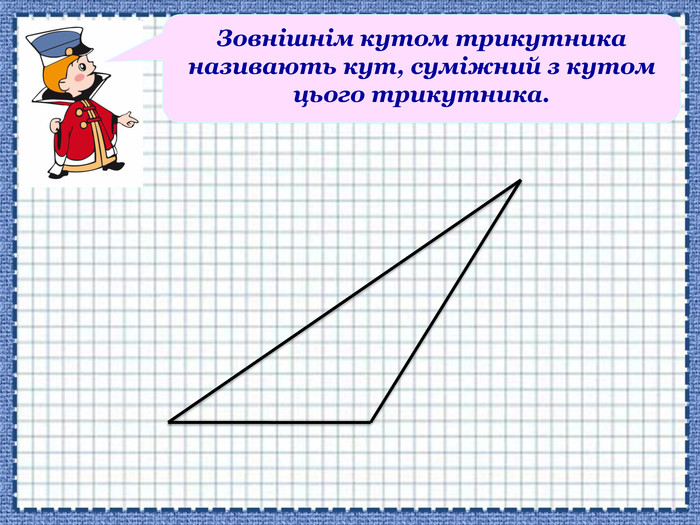


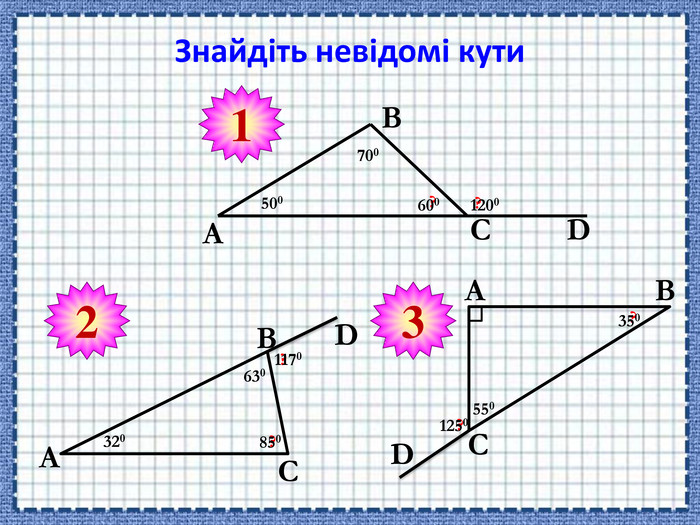

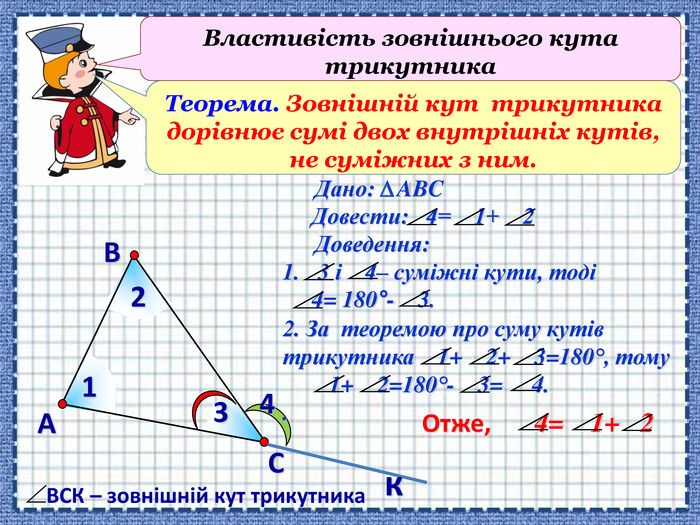


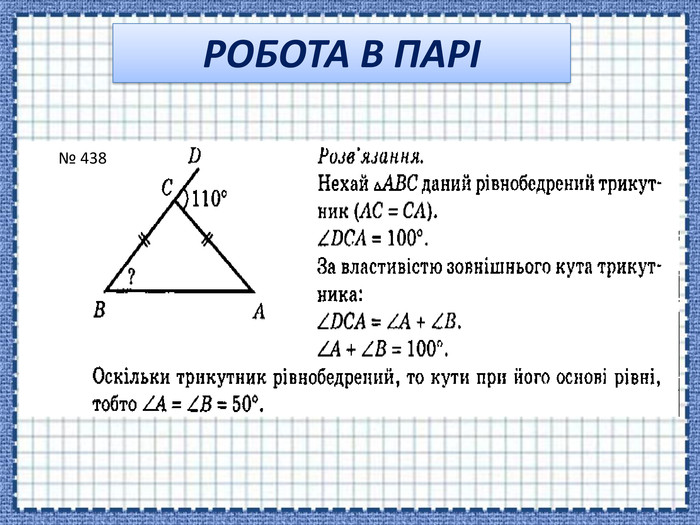








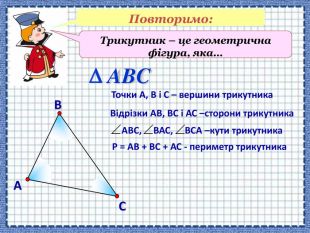







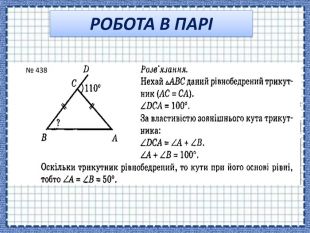




-

Мирошниченко Зоя Михайлівна
18.02.2025 в 08:00
Дякую.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вигоднер Діана Ісаківна
01.02.2024 в 21:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сухомлинова Анжела Миколаївна
08.01.2023 в 20:40
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Крутько Світлана
07.01.2023 в 22:32
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kr Elena
22.02.2022 в 17:45
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гороховець Ніна Іванівна
14.02.2022 в 14:48
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Зеніна Світлана Савеліївна
09.02.2022 в 21:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Дімнич Надія
02.02.2022 в 20:11
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тодоренко Оксана Василівна
18.01.2022 в 21:57
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сергєєва Галина Віталіївна
08.03.2021 в 19:20
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Забродська Олена Валентинівна
17.02.2021 в 09:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ирина Ирина
21.01.2021 в 19:02
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Олійник Ольга Миколаївна
21.01.2021 в 11:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 10 відгуків