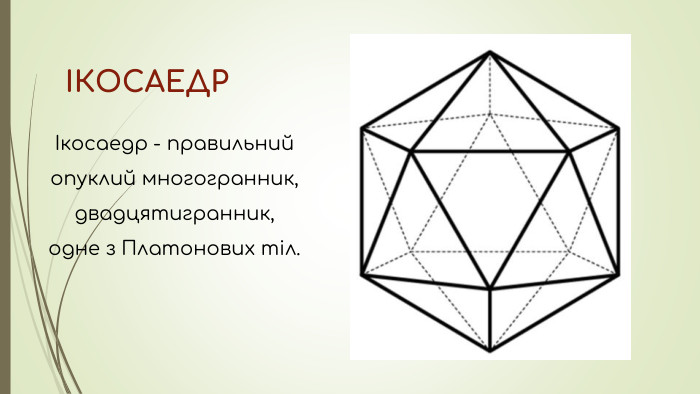
Презентація "Ікосаедр"
Про матеріал
Презентація "Ікосаедр" знайомить учнів з одним із найзагадковіших і найкрасивіших правильних многогранників – ікосаедром. У доступній формі пояснюються основні поняття, пов'язані з ікосаедром: грані, ребра, вершини, симетрія. Яскраві ілюстрації та приклади з реального життя допоможуть учням краще уявити цю геометричну фігуру та її властивості. Перегляд файлу
Зміст слайдів
pptx
До підручника
Геометрія (академічний, профільний рівень) 11 клас (Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку