Уроку в 11 класі "Піраміда"
Тема уроку: Піраміда. Розв’язування задач
Мета:
навчальна: повторити, поглибити та систематизувати знання про піраміду, теорему про площу бічної поверхні піраміди, алгоритм розв’язування задач, використовуючи властивості піраміди;
виробити навички і вміння розв’язувати задачі, використовуючи властивості піраміди;
розвиваюча: розвивати культуру математичної мови і пізнавальний інтерес, застосування в різних галузях знань;
виховна: виховувати інтерес до геометрії, працьовитість, прищеплювати бажання мати якісні і глибокі знання.
Обладнання: моделі піраміди, роздатковий матеріал, комп’ютер, мультимедіа.
Тип уроку: узагальнення знань, умінь та навичок
Хід уроку
Знання можуть бути купою каміння, що
задавила особистість. І знання можуть бути
вершиною піраміди на якій стоїть
особистість.
І Організаційний етап..
ІІ. Мотивація навчальної діяльності.
Піраміда – дуже цікава фігура не тільки з точки зору математики, а ще і як унікальний витвір всесвітньої культури.
Перше із семи див світу - ПІРАМІДА.
За давніх часів піраміди вважалися першими із семи див світу. І, виходячи з того, що нам відомо про інші шість чудес, можна сказати: для цього були всі підстави – піраміди і досі вважаються дивом із див! І хоч ми споруджаємо телевізійні вежі, куди вищі, а стадіони – куди більші, ніж найвища і найбільша із пірамід, - за компактно забудованою площею й масивністю її поки що не перевершила жодна новітня споруда.
ІІІ. Повідомлення теми і мети уроку
ІV. Актуалізація опорних знань.
1. Інтерактивна технологія « Закінчи речення» - усно.
1. Многогранник, який складається з плоского многокутника, точки, яка не лежить у площині плоского многокутника і всіх відрізків, що сполучають цю точку з точками плоского многокутника називається… ( пірамідою )
2. Точка, яка не лежить у площині основи піраміди називається…(вершиною)
3. Відрізки, що сполучають вершину піраміди з вершинами основи, називаються…
( бічними ребрами)
4. Кожна бічна грань піраміди є… ( трикутник )
5. Перпендикуляр, опущений з вершини піраміди на площину основи називається…
( висотою піраміди )
6. Чотирикутна піраміда має ребер… ( вісім )
7. Трикутну піраміду називають … (тетраедром)
8. Поверхня піраміди складається… ( з основи і бічних граней )
9. Піраміда називається правильною, якщо її основа є… (правильний многокутник , а основа висоти збігається з центром цього многокутника)
10. У правильній піраміді бічні ребра… ( рівні )
11. У правильній піраміді бічні грані рівні … ( рівнобедрені трикутники )
12. Висота бічної грані піраміди, проведена з її вершини, називається…(апофемою)
2. Фронтальна бесіда.
1. Яка ж піраміда називається правильною?
2. Сформулюйте властивості правильної піраміди.
3. Назвіть алгоритм побудови правильної піраміди.
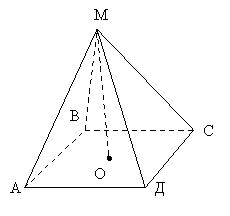
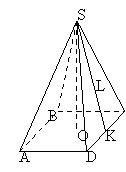
АВСД – основа піраміди
М - вершина
МА, МВ, МС, МД – бічні ребра
▲МАВ, ▲МВС, ▲МСД, ▲ МАД – бічні грані.
МО – висота.
3. види пірамід:
а) Піраміди характеризуються за кількістю сторін в основі. Піраміда називається n – кутною, якщо її основою є n – кутник.
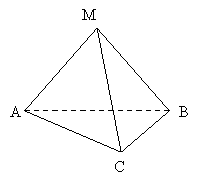
Трикутна піраміда називається також тетраедром:
Чотирикутна піраміда:
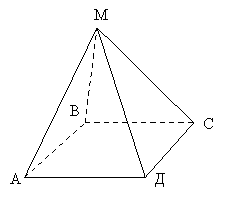
б) Піраміди бувають правильні і неправильні. Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника.
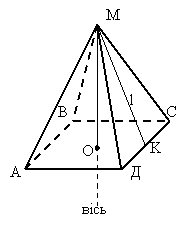
Правильна чотирикутна піраміда.
пряма МО - вісь
відрізок МО - висота
L - Апофема
АВСД – квадрат
Неправильна чотирикутна піраміда
На дошці крейдою вчитель, а учні в зошитах будують правильну чотирикутну піраміду.
АЛГОРИТМ ПОБУДОВИ ПРАВИЛЬНОЇ ЧОТИРИКУТНОЇ ПІРАМІДИ
- Будуємо паралелограм АBCD;
- Знаходимо точку перетину діагоналей – точку О;
- Проводимо висоту SO (S - вершина);
- Сполучаємо вершину з точками основи;
правильно побудована піраміда неправильно побудована піраміда
Бічна поверхня піраміди – сума площ бічних граней.
Теорема 5.6.
Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.
Sбічн
Довести, що Sбічн 
На дошці крейдою:
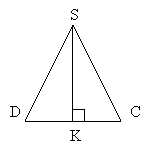
S▲DSC=1/2 DC•SK
Sбічне = 4•S▲
Sбічне =4•1/2•DC•SK=4•DC•1/2•P•L
Sбічне=1/2•Ρ•L
Sповне =Sоснови +Sбічне
- Застосування тіл пірамідальної форми в навколишньому середовищі. Тіла пірамідальної форми зустрічаються в будівництві, архітектурі. У вигляді шести- та восьмигранних пірамід (повних та зрізаних) будують каплички (невеликі церкви) та великі церковні храми. Дахами пірамідальної форми прикрашають кіоски, альтанки, «грибочки».
У формі правильної чотирикутної піраміди роблять ковпаки над димоходами, щоб атмосферні опади не потрапляли в димохідну трубу.
Музей сучасного мистецтва в Карасі (Венесуела) має форму перевернутої піраміди.
А в живописному березовому гаї Підмосков’я збудований комплекс молодіжного олімпійського табору. Його корпуси мають форму тригранних пірамід, дві бічні грані яких перпендикулярні до основи.
Економний і практичний фундамент для будов сільськогосподарського призначення запропонували вчені інженерно-будівельного інституту. Він являє собою піраміду зі залізобетону, забиту в землю вершиною вниз. Така конструкція здатна добре переносити й вертикальні, й горизонтальні навантаження. При цьому не треба рити котлован, зводити фундамент. На таких «ногах» міцно стоять будинки й тваринницькі приміщення уже в багатьох областях.
- Одного разу до відомого математика А. М. Колмогорова звернулися будівельники однієї з гідроелектростанцій за порадою. Вони повідомили, що швидка течія річки не дає змоги перекрити її русло звичайним способом. Тому будівельники хотіли знати, якою повинна бути форма кам’яних брил, щоб зупинити швидку течію річки.
Вчені зробили відповідні розрахунки і встановили, що річку потрібно перекрити бетонними тетраедрами. Крім того, вони підрахували, що таких тетраедрів повинно бути 7 500 штук.
Щоб уникнути помилки, будівельники спочатку подвоїли цю цифру, а потім добавили ще. Приготували на березі 35 тисяч пірамід. Кинули в річку 7 500 штук, а решта залишилися лежати на березі річки як пам’ятник невірам у математику.
У формі правильної піраміди роблять бункери для приготування розчину в будівельній справі. Таку ж форму мають і бункери зернозбиральних комбайнів.
А французький інженер Фелікс Шамайко здійснив тристакілометрову подорож по Нілу на судні власної конструкції. Його «Анітрон» має чітку форму піраміди. За словами винахідника, вона вибрана не випадково. Він вважає, що піраміда – це символ спадковості в інженерній думці.
Ажурну алюмінієву пірамідальну конструкцію утримують 32 пустотілі кулі і не дають судну перекидатися під час шторму.
Багато пам’ятників споруджують у вигляді піраміди. Так, пам’ятник Вічної слави, який споруджено у київському парку на схилі Дніпра — це обеліск, верхня частина якого має форму правильної чотирикутної піраміди.
- Я хочу нагадати про найдивніші споруди; що збереглися від стародавнього світу, — єгипетські піраміди. Серед них особливе місце посідає велика піраміда фараона Хеопса. Дослідники вважають, що в ній зашифровані знання тих часів з математики, астрономії тощо. Дивує точність інженерних розрахунків стародавніх зодчих.
Блоки, з яких складена піраміда, так точно підібрані один до одного, що між ними не проходить навіть лезо ножа.
У цій піраміді має місце теорема Піфагора, золота пропорція та ін.
Сьомий учень
А я хочу розповісти про те, що відомий німецький поет Гете вважав піраміду таємничою містичною фігурою. Про це писав і біограф Гете — Іммерман. Але у своїх спогадах про Гете німецький письменник припустився однієї математичної помилки. Ось послухайте, що він пише: «Одного разу я відвідав Гете і застав його в. робочому кабінеті за цікавою роботою. Поет виготовив з картону трикутник і хотів на ньому продемонструвати співвідношення між душевними силами людини. Чутливість він вважав основою серед усіх інших рис. Тому зобразив її в основі трикутника і зафарбував у зелений колір. Зафарбована в червоний колір бічна грань зображала фантазію, а в жовтий — здоровий глузд, у блакитний — розум.
По-перше, трикутник не мав граней, а мав сторони. По-друге, їх не чотири, а всього — три. Тож Іммерман припустився помилки. Гете, очевидно, виготовляв не трикутник. А що ж виготовляв поет? (Трикутну піраміду).
Восьмий учень розповість про застосування піраміди в медицині.
Піраміда золотого перерізу Ю.Шінсе виготовлена із спеціального матеріалу і відтворює геометричні параметри давньоєгипетської піраміди Хеопса (до речі, за параметрами золотого перерізу побудовані також всі храми).
Принцип золотого перерізу дозволяє концентрувати енергію геомагнітної піраміди, тонких енергоінформаційних потоків – їх частота набагато перевищує частоти, якими оперує сучасна фізика. До того ж золота піраміда дійсно покрита золотом - молекули цього дорогоцінного металу вібрують на тій же частоті що і структури здорових клітин людського організму. Недарма на іконах німби у святих золоті, як і купола більшості соборів.
Згідно результатів клінічних досліджень, піраміда має стимулюючу дію на органи і системи пацієнтів, коректує їх функціональний стан.
Піраміда Ю. Шінсе лікує гіпертонію, хвороби серця, покращує формулу крові, виводить з депресивного стану, поліпшує стан хворих цукровим діабетом, зменшує болі в суглобах та м’язах.
Піраміда Ю.Шінсе не тільки покращує здоров’я дітей, але і позитивно впливає на їх психологічний стан, профілактику захворювань і здатність до навчання (показник відмінних робіт по Україні підсумкової атестації учнів складає 30 – 33%, а дітей, на яких діяла піраміда Ю.Шінсе 60 – 70 %).
Піраміда підвищує енергетичний потенціал, гармонізує відношення між членами родини, проблеми батьків-дітей.
VІ. Закріплення навичок і вмінь у розв’язуванні задач.
1. Усно. Завдання «пастка». (Зображені трикутна піраміда, чотирикутна піраміда, трикутна призма).
1. Як називається кожна піраміда?
2. З яких елементів вона складається?
3. Скільки вершин має n-кутна піраміда? (n+1)
4. Скільки ребер має n-кутна піраміда? (2n)
2. Два учні працюють з картками.
|
Картка № 1
а) 8 б) 7 в) 14 г) 15 д) 21 2. Площа повної поверхні правильної трикутної піраміди дорівнює 64 см2, а площа її основи – 25 см2. Знайдіть площу однієї бічної грані піраміди. 3. Знайдіть площу повної поверхні правильної трикутної піраміди, кожне ребро якої дорівнює а. 4. Основою піраміди є прямокутник, діагональ якого дорівнює 8 см. Площини двох бічних граней піраміди перпендикулярні до площини її основи, а дві інші грані утворюють із площиною основи кути 30° і 45°. Знайдіть площу бічної поверхні піраміди. |
|
Картка № 2
а) 12 б) 24 в) 9 г) 8 д) 16 2. У правильній трикутній піраміді площа однієї бічної грані дорівнює 8 см2, а площа основи – 12 см2. Знайдіть площу повної поверхні піраміди. 3. Знайдіть площу повної поверхні правильної чотирикутної піраміди, кожне ребро якої дорівнює а. 4. Основою піраміди є прямокутник, діагональ якого дорівнює 12 см. Площини двох бічних граней піраміди перпендикулярні до площини її основи, а дві інші грані утворюють із площиною основи кути 60° і 45°. Знайдіть площу бічної поверхні піраміди. |
3. . Робота біля дошки
1. Висота правильної чотирикутної піраміди дорівнює 3 см, а бічне ребро – 5 см. Визначте косинус кута між бічним ребром піраміди і площиною її основи.
4.Робота в групах.
І група (слабші учні) – самостійно.
Висота правильної чотирикутної піраміди дорівнює 4 см, а її апофема – 5 см. Визначте косинус кута між площиною бічної грані піраміди і площиною її основи.
ІІ група (сильніші учні) – робота біля дошки.
Основою піраміди є квадрат зі стороною 6 см, а основою висоти піраміди – точка перетину діагоналей квадрата. Знайдіть довжину бічних ребер піраміди і площу повної поверхні цієї піраміди, якщо її висота дорівнює 8 см.
ІІ група (сильніші учні) – самостійно.
Основою піраміди є прямокутник зі сторонами 6 см і 8 см. Кожне бічне ребро піраміди дорівнює 13 см. Обчисліть висоту піраміди.
І група (слабші учні) - робота біля дошки.
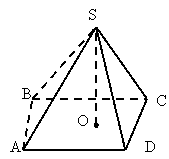
За зображеною пірамідою SABCD заповніть пропуски.
SABCD - ………… піраміда.
SО – ……….. піраміди.
ABCD - ………
SCD - ………..
SB - ………….
SК - ………….
VІІ. Підсумок уроку.
1. Сьогодні на уроці я повторив…
2. Сьогодні на уроці я зрозумів…
3. Переконався, що необхідно додатково попрацювати над…
4. Найважчим для мене було…
VІІ. Домашнє завдання.
п. 16 ст. 128 (повторити), № 17, № 19 ст. 139
Підготувати інформацію:
І група - «Практичне використання властивостей піраміди»
ІІ група – «Вислови про піраміду»
Виконання практичних завдань.
Тепер вашій увазі пропоную кілька задач і запитань.
- «Мені потрібно склеїти з картону модель правильної піраміди, в основі якої лежить ромб з гострим кутом 60°, а всі бічні ребра рівні між собою», - сказав Микола. «Такої піраміди не існує», - заперечив Іван. Чи правильне твердження Івана?
- Які виміри треба зробити, щоб визначити висоту моделі правильної піраміди? Які треба зробити обчислення?
-
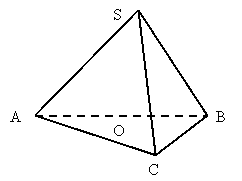Піраміда має рівні бічні ребра. В яку точку основи, що становить прямокутний трикутник, проектується вершина піраміди?
-
Дано правильну трикутну піраміду. Побудуйте кут:
- між бічним ребром і площиною основи;
- між бічною гранню і площиною основи;
Практична робота
- На кожен стіл (двом учням) видається модель правильної піраміди. Потрібно зробити малюнок, відповідні виміри і обрахувати висоту піраміди. Завдання виконується в робочих зошитах.
V. Підведення підсумків уроку. Оцінювання учнів.
VІ. Домашнє завдання: О.В. Погорєлов «Геометрія 10-11»
§ 5 п. 27, 31, 32, 33, 34; №69
про публікацію авторської розробки
Додати розробку