Презентація "Комбінації"
Про матеріал
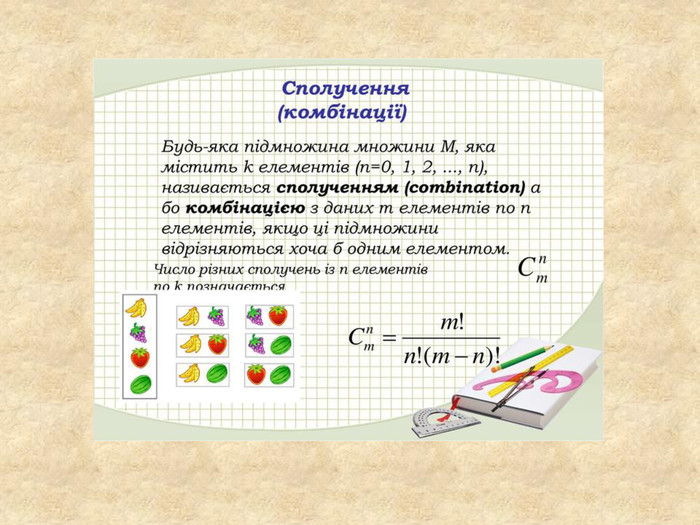
Матеріал для ознайомлення з формулами комбінаторики,містить задачі на комбінації елементів. Містить приклади розвязування таких задач та завдання для самостійного розвязування. Перегляд файлу
Зміст слайдів
ppt
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
21. Основні правила комбінаторики Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку