Презентація "Комбінаторика та елементи стохастики в шкільному курсі математики"

Комбінаторика та елементи стохастики в шкільному курсі математики

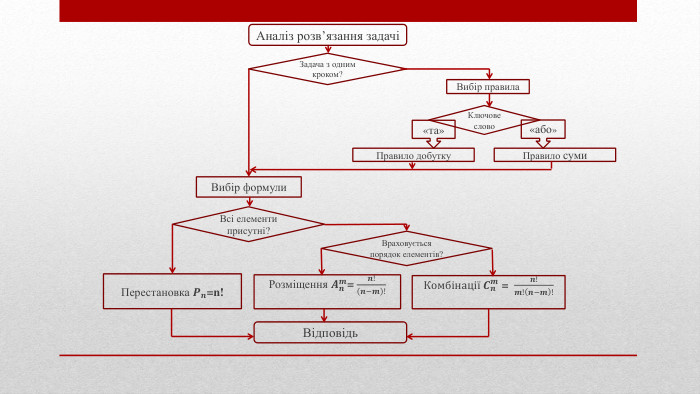
КОМБIНАТОРИКА - це розділ математики, в якому вивчаються прості "сполуки" : перестановки, розміщення, комбінації.(Великий Енциклопедичний Словник) -походить від латинського слова "combina", що в перекладі означає - "поєднувати", "сполучати".-Розділи комбінаторики : Перелічувальна. СтруктурнаІмовірнісна. Топологічна

Задача P = 4! = 1 * 2 * 3 * 4 = 24 Пустунка Мавпа. Осел. Козел. Та клишоногий Ведмедик. Затіяли грати квартет. Стій, братики стій! -Кричить Мавпа, - почекайте!Як музиці йти?Адже ви не так сидите.І так, і отак пересідали - знову музика на лад не йде. Ось більше колишнього пішли у них розбориІ спори. Кому і як сидіти. Скількома способами можна розсадити чотирьох музикантів?:

«Скількома способами…?» Особлива прикмета комбінаторних задач - питання, що починалося словами:-

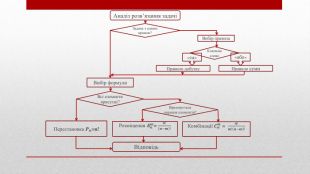
Перестановки – цесполуки, які можна скласти з n предметів, змінюючи всіма можливими способами їх порядок; Число їх Число n називається порядком перестановки. n-факторіалце добуток всіх натуральних чисел від одиниці до n, позначають символом ! Використовуючи знак факторіала ! , можна, наприклад, записати:1! = 1,2! = 2*1=2,3! = 3*2*1=6,4! = 4*3*2*1=24,5! = 5*4*3*2*1 = 120. Необхідно знати, що 0! = 1

Розміщення – сполуки, що містять по m предметів з числа n даних, клтрі розрізняються або порядком предметів, або самими предметами; число їх

Задача. В класі навчається 24 учні. Сколькома способами можна скласти графік чергування по классу, якщо група чергових включає три учні?Розв’язання задачі: Відповідь: кількість способів дорівнює числу розміщень з 24 по 3; 12144 способи.

Комбінації–сполуки,що містять по m предметів із n, котрі відрізняються одна від одної, меншою мірою, одним предметом; число їх

Задача. Учням надали список з 10 підручників, які рекомендовано використати для підготовки до екзамену . Сколькома способами учень може вибрати із них 3 книги?

Розв’язання задачі: Відповідь: число способів дорівнює числу комбінацій з 10 по 3; 120 способів.

Аналіз розв’язання задачіКлючове слово. Задача з одним кроком?«та»«або»Вибір правила. Правило добутку. Правило суми. Вибір формули. Всі елементи присутні?Перестановка 𝑷𝒏=n!  Враховується порядок елементів?Розміщення 𝑨𝒏𝒎= 𝒏!𝒏−𝒎!  Комбінації 𝑪𝒏𝒎 = 𝒏!𝒎!𝒏−𝒎!  Відповідь

Електротехнiка. В коридорі висить три лампочки. Скільки мається різних способів освітлення коридору?

Гра Шахи. Видатні шахісти Клод Шеннон та Михайло Ботвінник зробили величезний внесок у створення математичної моделі шахової гри та сприяли прогресу в інтелектуалізації програм для неї. Комп'ютерні шахи — чи не найпереконливіший приклад за півстоліття розвитку інформаційних технологій, коли саме в інтелектуальній діяльності автомат успішно змагається з людиною.

Словникь. Терміном стохастика (від грец. Stоhastikos - вміє вгадувати, випадковий) поєднують розділи математики, що вивчають випадкові явища: теорію ймовірностей, математичну статистику, теорію ігор, теорію випадкових процесів та ін. Теорія ймовірностей – розділ математики, вивчає закономірності виникнення випадкових явищ. Статистика - наука, що вивчає кількісні показники розвитку суспільства та суспільного виробництва, кількісний облік різноманітних масових випадків, явищ (с. народжуваності, статистика знає все (афоризм))Математична статистика – наука про математичні методи систематизації та використання статистичних даних

Ймовірність. ТЕОРIЯ ЙМОВІРНОСТЕЙ ДАЄ СПОСІБ ЗНАХОЖДЕНИЯ КІЛЬКІСНОГО ЗНАЧЕННЯ ЙМОВІРНОСТІ ПОДІЇ: А – деяка подія,m – кількість випадків, при яких подія А відбувається,n – число рівноможливих випадків. P – позначення походить від першої літери французького слова probabilite – ймовірність.

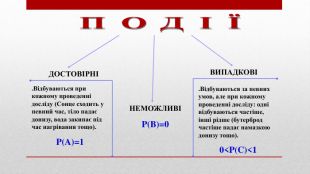
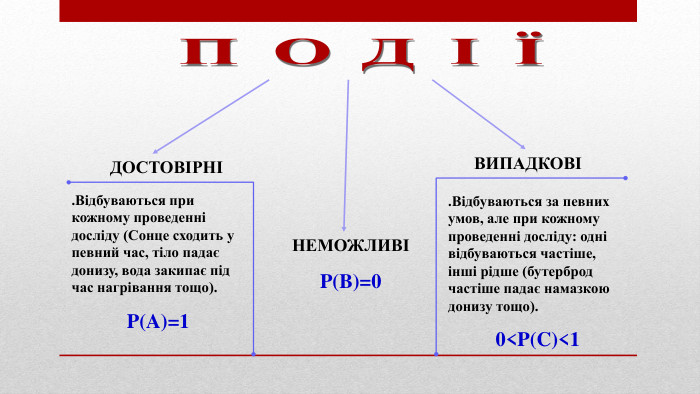
ПОДІЇДОСТОВІРНІВИПАДКОВІ. Відбуваються при кожному проведенні досліду (Сонце сходить у певний час, тіло падає донизу, вода закипає під час нагрівання тощо). P(A)=1. Відбуваються за певних умов, але при кожному проведенні досліду: одні відбуваються частіше, інші рідше (бутерброд частіше падає намазкою донизу тощо).0

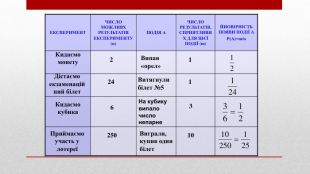
ЕКСПЕРИМЕНТЧИСЛО МОЖЛИВХ РЕЗУЛЬТАТІВ ЕКСПЕРИМЕНТУ (n)ПОДІЯ АЧИСЛО РЕЗУЛЬТАТІВ, СПРИЯТЛИВИХ ДЛЯ ЦІЄЇ ПОДІЇ (m)ЙИОВІРНІСТЬ ПОЯВИ ПОДІЇ АР(А)=m/n. На кубику випало число непарне. Кидаємо монету2 Випав «орел»1 Дістаємо екзаменаційний білет. Витягнули білет №5241 Кидаємо кубика63 Приймаємо участь у лотереїВиграли, купив один білет25010

статистика. З карток склали слово «статистика». Яку картку з буквою найімовірніше витягнути? Які події є рівноймовірними?

Статистичні характеристики. Середнє арифметичне є частка від розподілу суми всіх варіант вибірки до загальної кількостіРозмах вибірки – різниця між найбільшою та найменшою варіантами вибірки: r = Xmax-Xmin. Модою вибірки називається найчастіше зустрічається її варіанта. Як визначити моду? Якщо вибірка представлена ​​таблицею частот, то визначення моди необхідно знайти максимальну частоту і назвати варіанту їй відповідну. Статистичний ряд може бути таким, що в ньому не одна мода чи взагалі моди немає. Медіана вибірки – це середнє значення у впорядкованому ряду варіант. Як обчислюється медіана Ме =? Якщо впорядкований статистичний ряд має непарне число варіант, медіаною буде число, записане посередині. Якщо число варіант парне, то медіана дорівнює напівсумі варіант, записаних посередині.

ПРИКЛАД Під час перевірки 70 робіт з української мови відзначали число орфографічних помилок, допущених учнями. Отримані результати подали у вигляді таблиці частот. Число помилок0123456частота46152612431) Яка найбільша відмінність у числі допущених помилок?Відповідь: розмах r =62) Яка кількість помилок вважається типовою для цієї групи учнів? Відповідь: Мо=33) Яке середнє число помилок припустився кожен учень?Відповідь: ср.ар. = (6 +30 +78 +48 +20 +18): 70 =4) Які статистичні показники були використані при відповіді на поставлені питання?

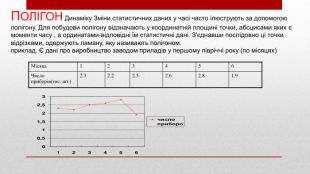
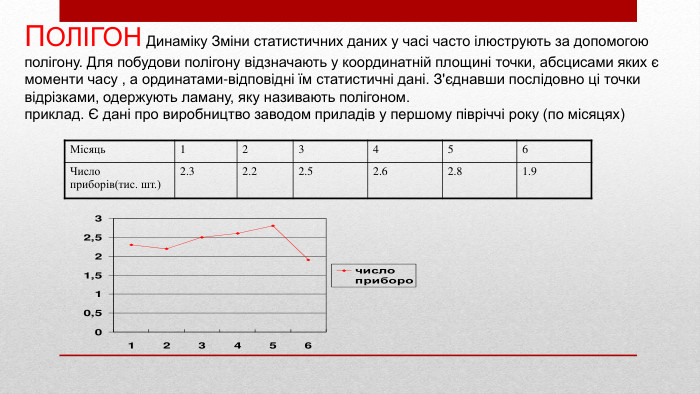
Місяць123456 Число приборів(тис. шт.)2.32.22.52.62.81.9 ПОЛІГОН Динаміку Зміни статистичних даних у часі часто ілюструють за допомогою полігону. Для побудови полігону відзначають у координатній площині точки, абсцисами яких є моменти часу , а ординатами-відповідні їм статистичні дані. З'єднавши послідовно ці точки відрізками, одержують ламану, яку називають полігоном.приклад. Є дані про виробництво заводом приладів у першому півріччі року (по місяцях)

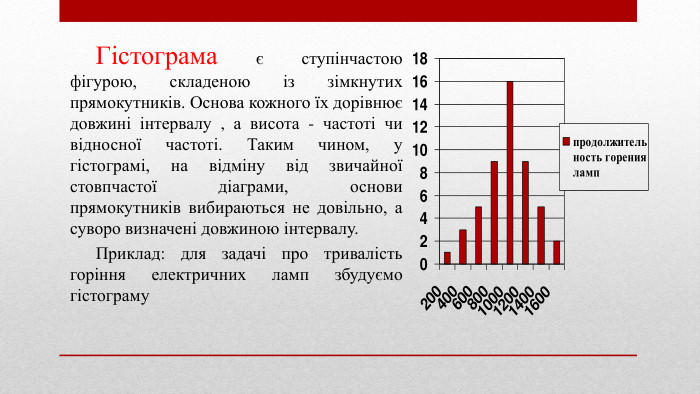
Гістограма є ступінчастою фігурою, складеною із зімкнутих прямокутників. Основа кожного їх дорівнює довжині інтервалу , а висота - частоті чи відносної частоті. Таким чином, у гістограмі, на відміну від звичайної стовпчастої діаграми, основи прямокутників вибираються не довільно, а суворо визначені довжиною інтервалу. Приклад: для задачі про тривалість горіння електричних ламп збудуємо гістограму

ВИСНОВОКПосилення інтересу до комбінаторики останнім часом обумовлюється бурхливим розвитком кібернетик. Велике значення у різних галузях науки та виробничій сфері. Розвиток математичних здібностей.Імовірнісно-статистичні закони – основа опису наукової картини світу. Посилення внутрішньопредметних зв'язків.