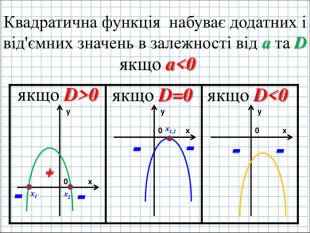
Презентація "Квадратична функція та її графік"
Про матеріал
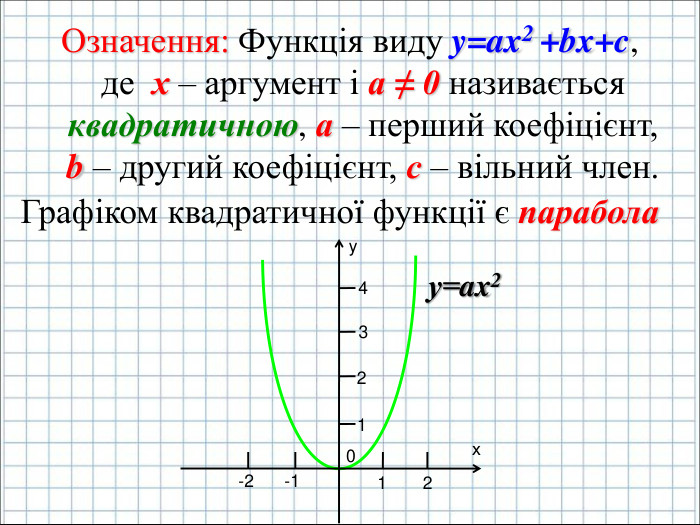
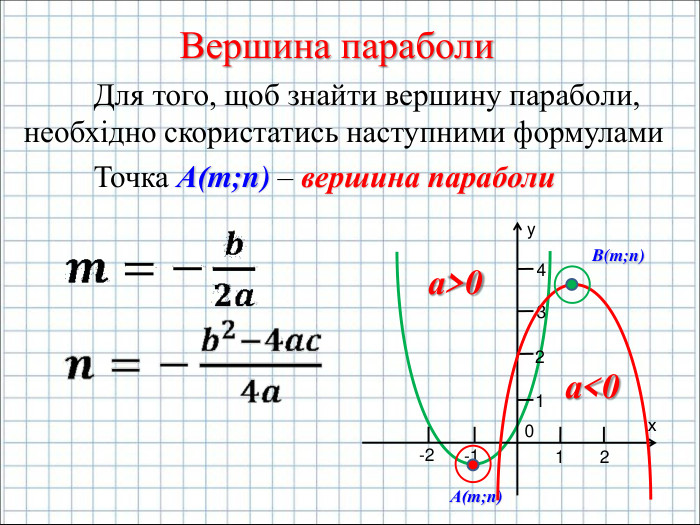
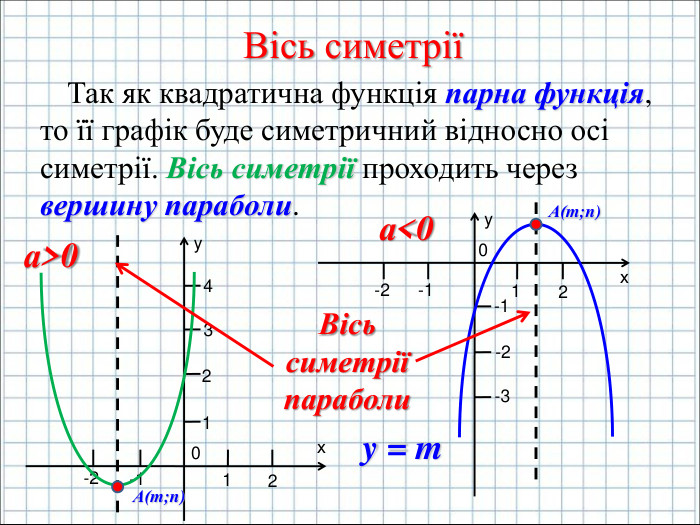
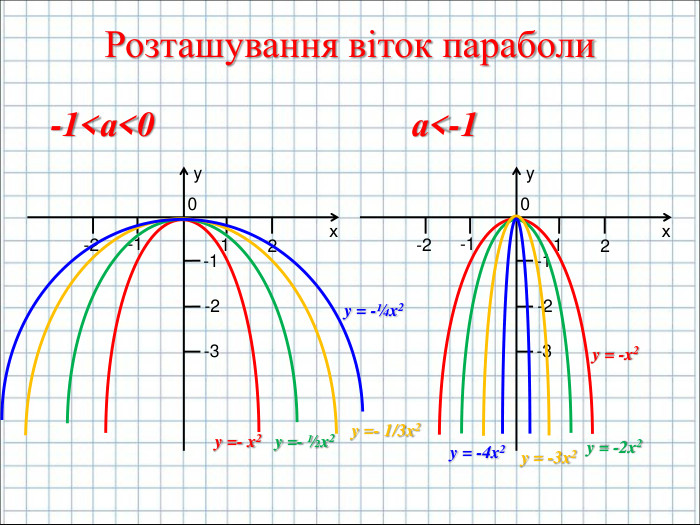
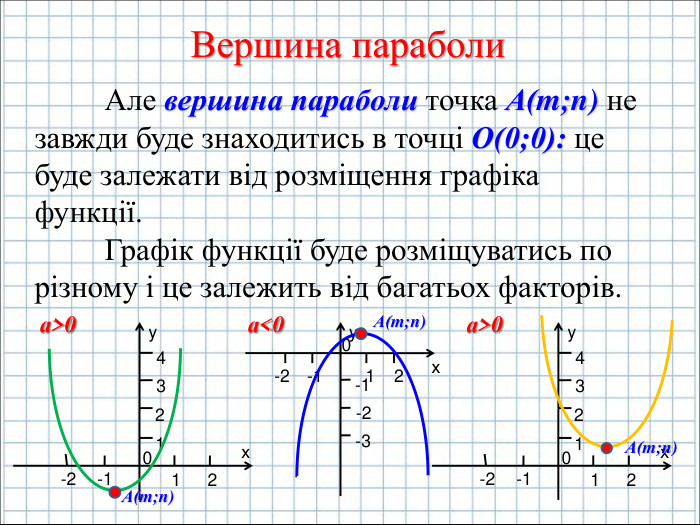
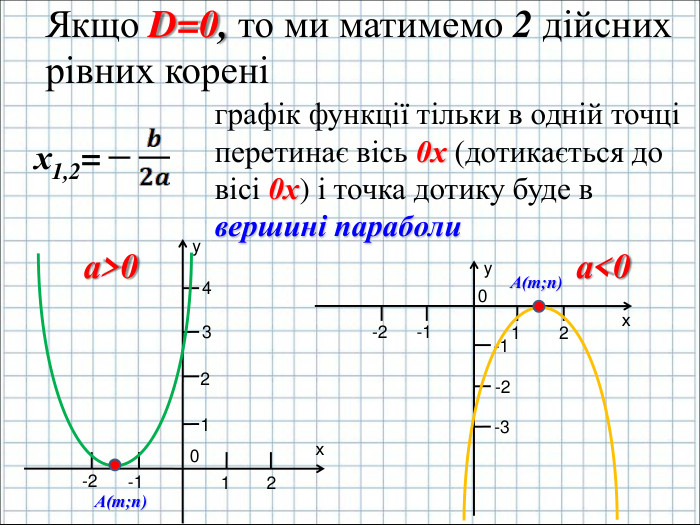
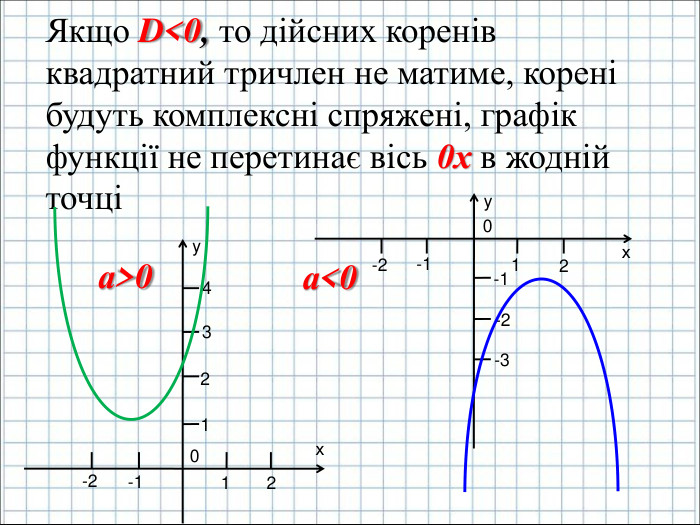
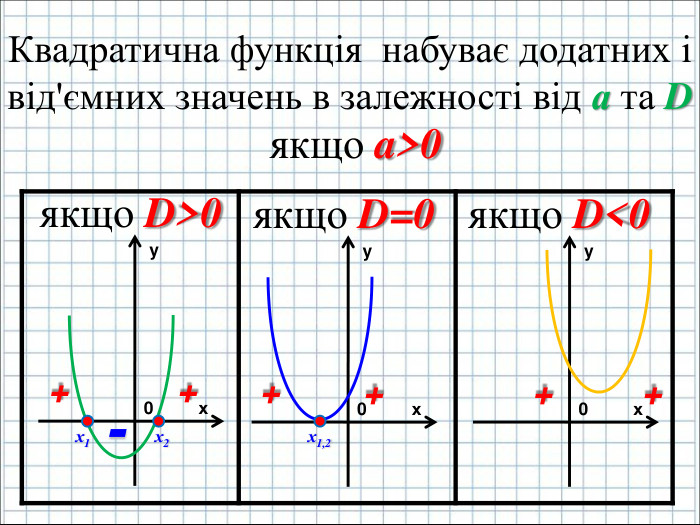
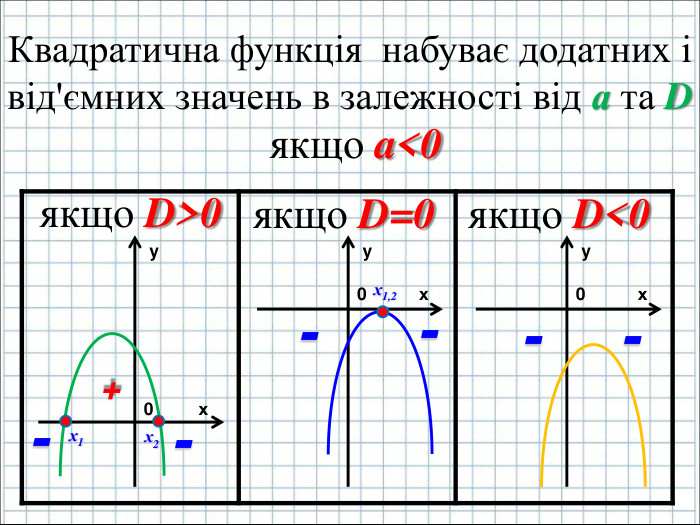
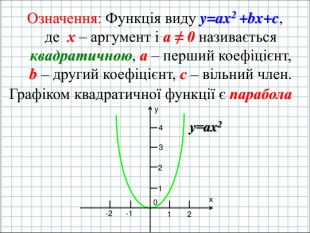
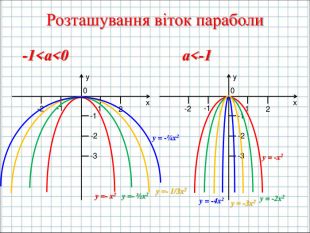
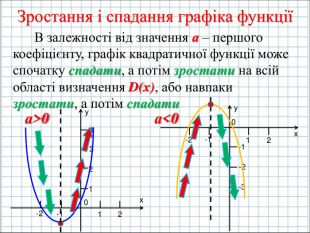
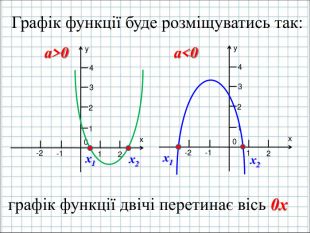
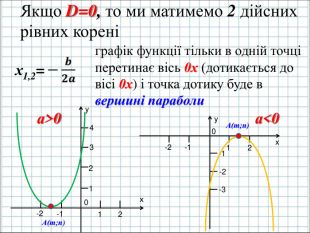
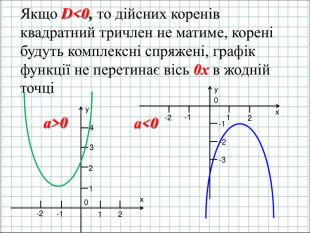
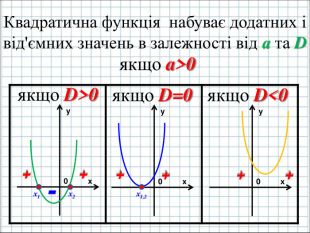
Ввести означення квадратичної функції; сформувати вміння учнів будувати графік функції y=ax2+bx+c(а ≠0); розвити навички розпізнавати квадратичну функцію серед інших елементарних функцій, знаходити координати вершини параболи та напрям віток графіка квадратичної функції, виконувати побудову графіка за визначеним алгоритмом. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку