Презентація на тему "Поняття функції, способи її задавання, властивості функції".
Про матеріал
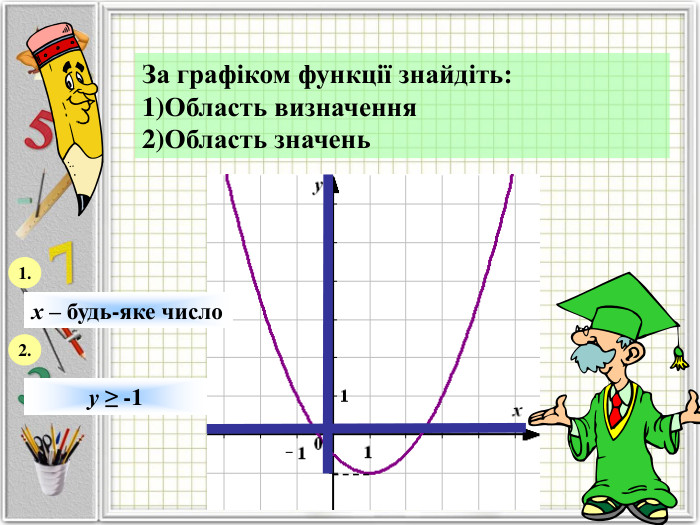
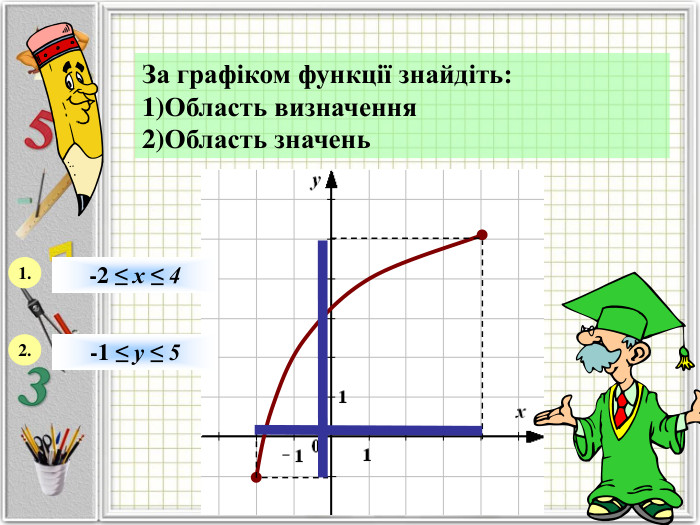
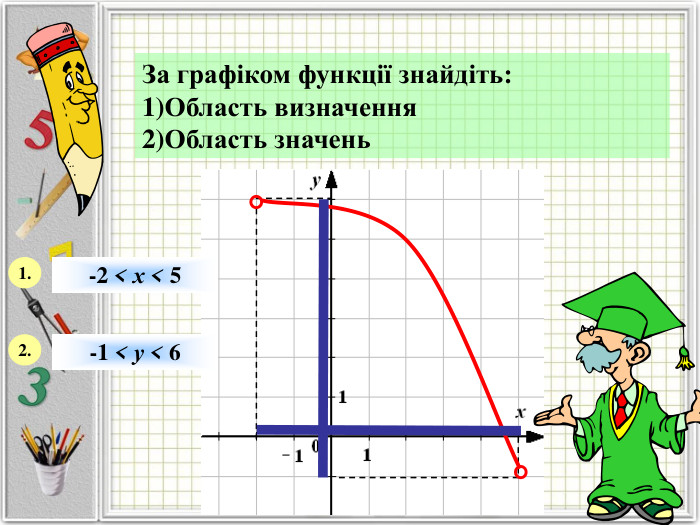
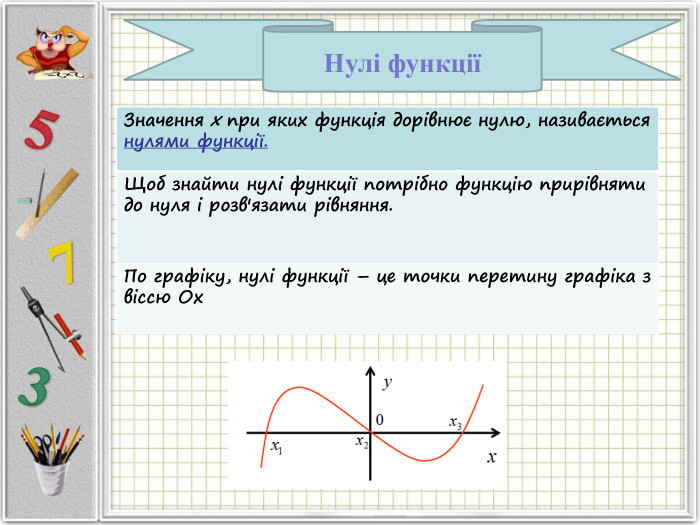
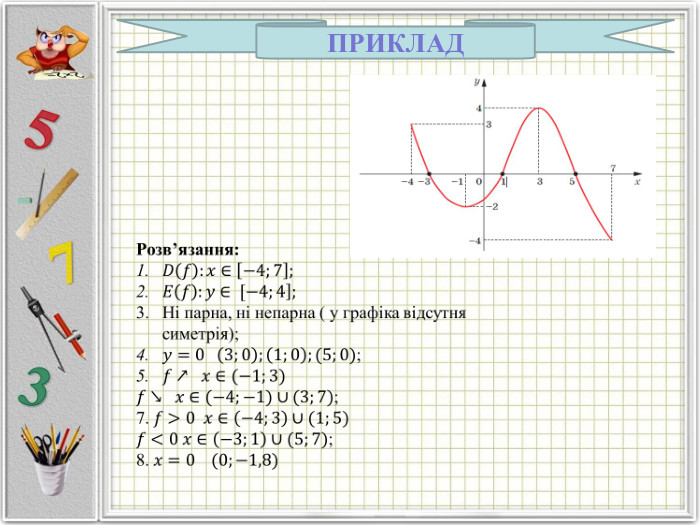
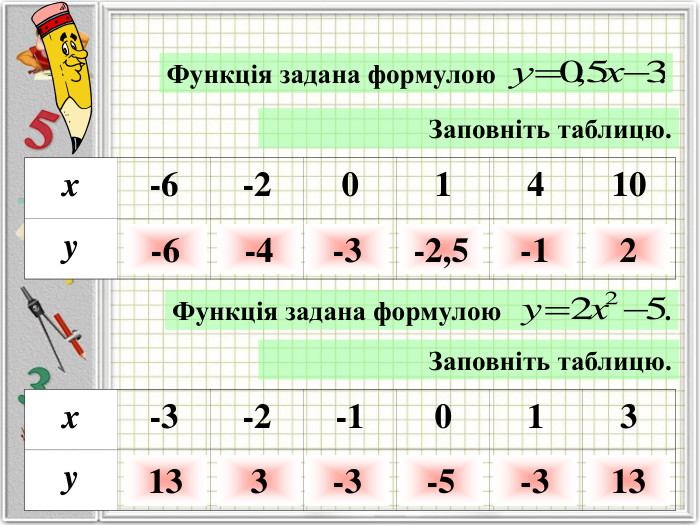
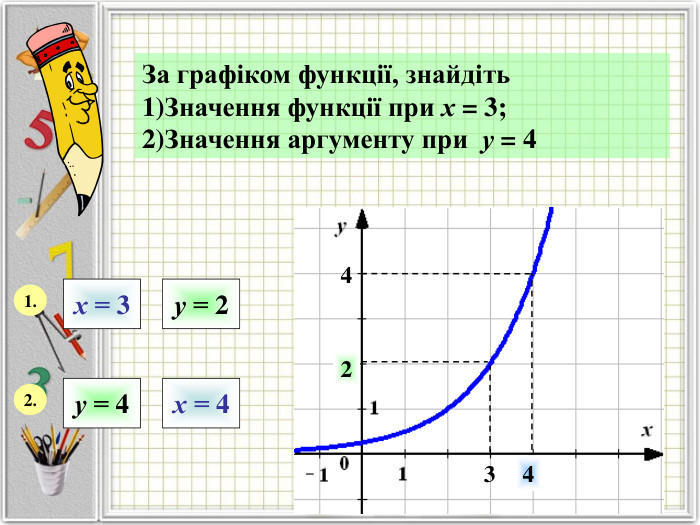
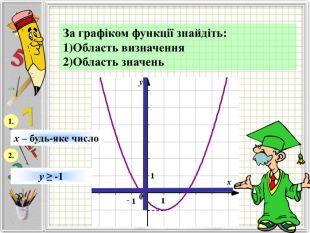
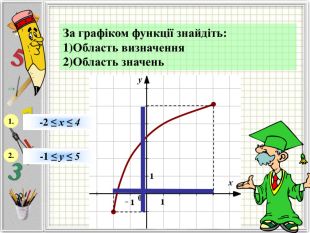
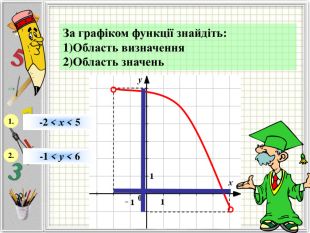
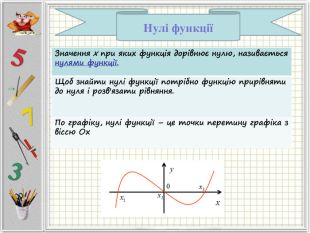
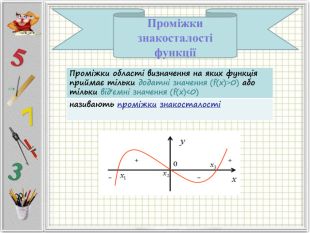
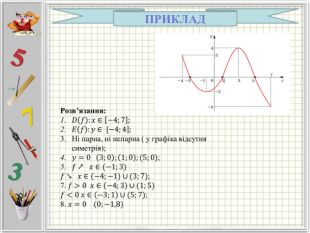
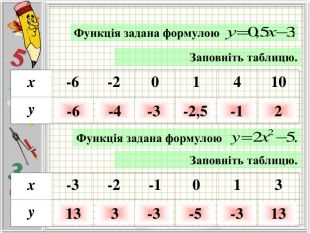
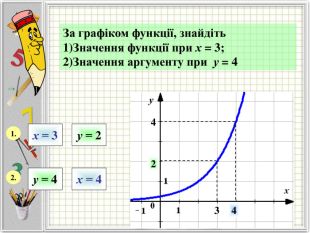
Означення функції, позначення і терміни, способи задання, графік, область визначення і область значень функції, монотонність функції, парність і непарність, нулі функції, проміжки знакосталості.
Наведення прикладів. Перегляд файлу
Зміст слайдів
ppt
До підручника
Алгебра 9 клас (Істер О. С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку