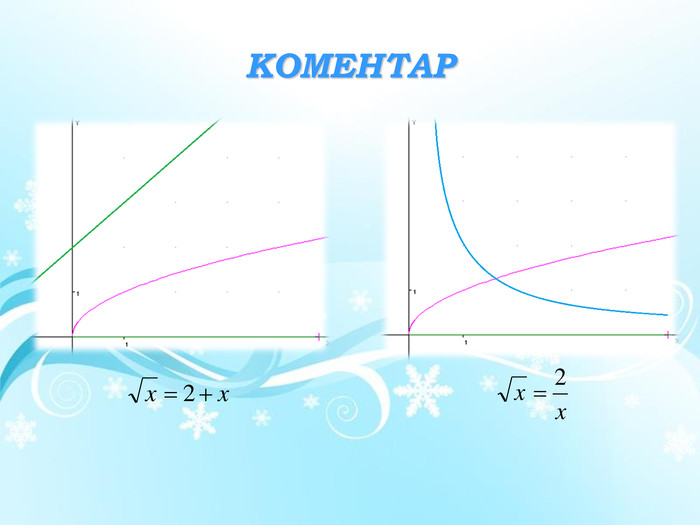
Презентація "Квадратні корені. Підсумковий урок"
Про матеріал
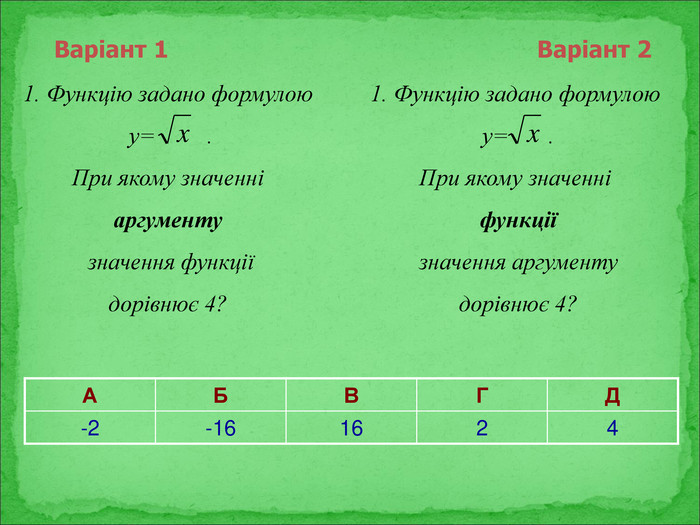
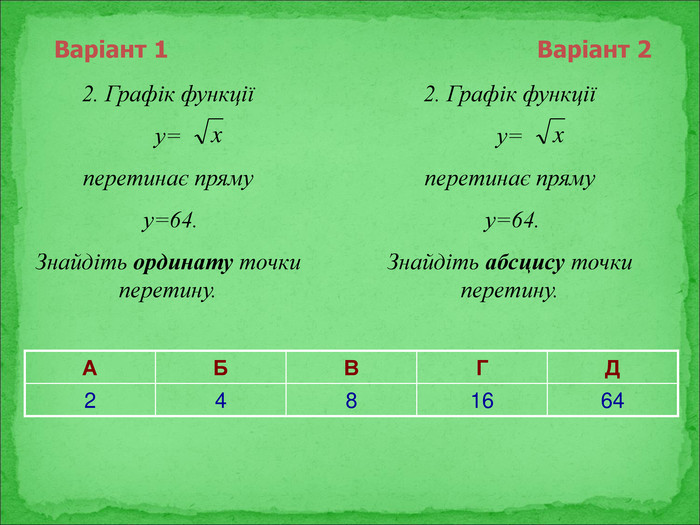
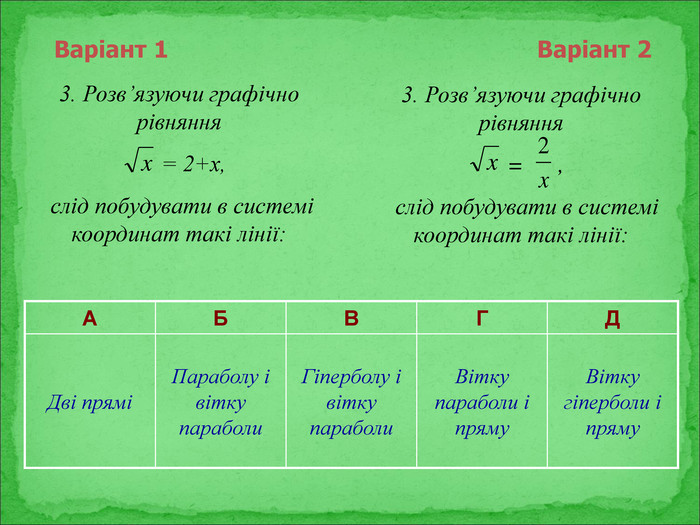
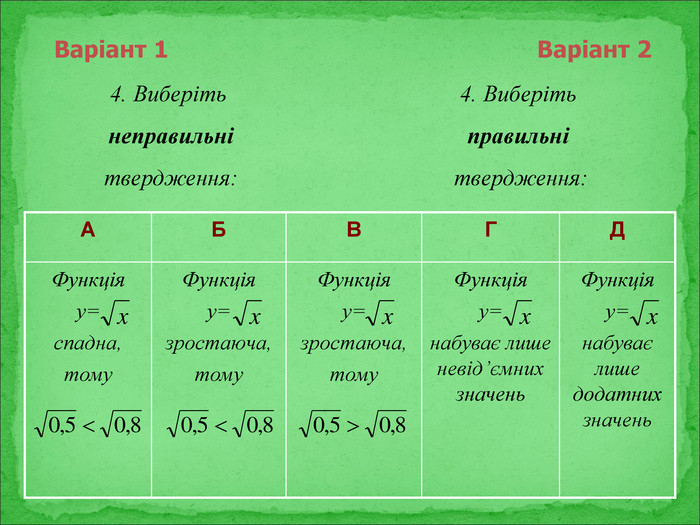
Презентація містить матеріали до підсумкового уроку теми "Квадратні корені".
Оцінювання проводиться по рівнях кольоровими балами-сердечками, оскільки урок припадає на період Дня закоханих.
Містить нестандартні історичні математичні задачі, софізм, а також експрес-тест із самоперевіркою. Перегляд файлу
Зміст слайдів
ppt
До підручника
Алгебра 8 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
§ 2. Квадратні корені. Дійсні числа Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку