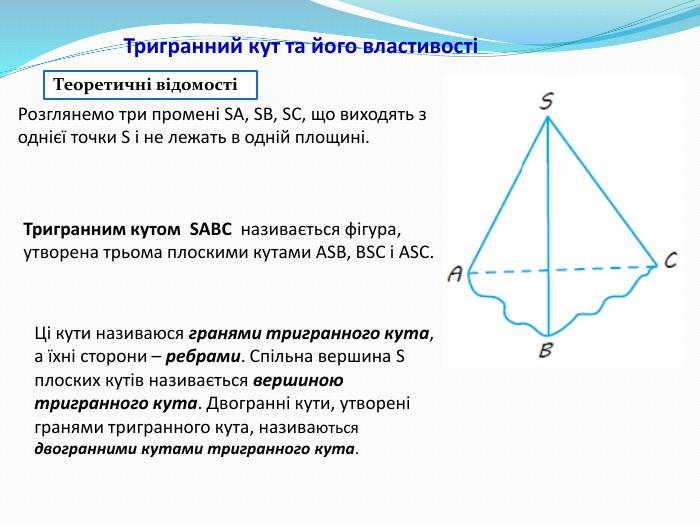
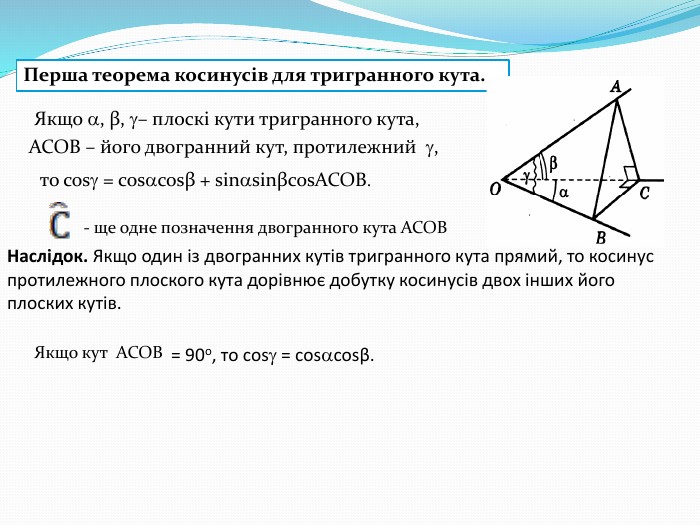
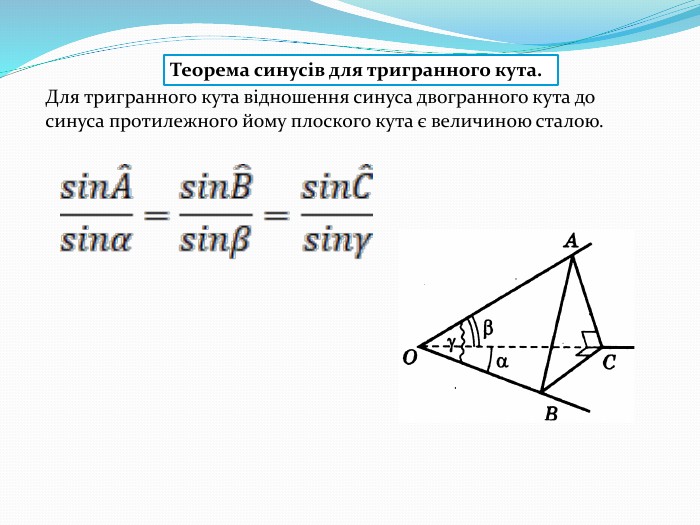
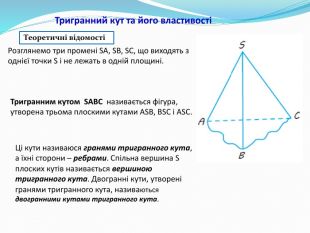
Презентація " Многогранні кути. Тригранний кут."
Про матеріал
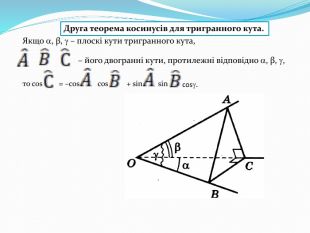
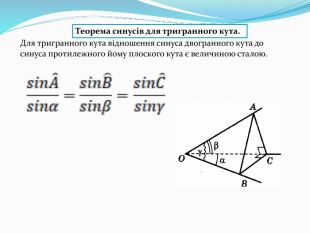
Презентація до уроку з геометрії для 11 класу (рівень стандарт) на тему: "Многогранні кути." Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку