Презентація "Многокутник та його елементи"
Про матеріал
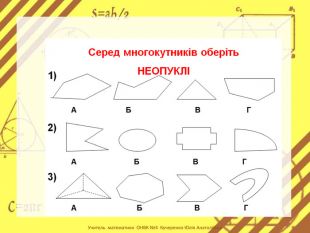
Презентація до теми "Многокутник та його елементи".
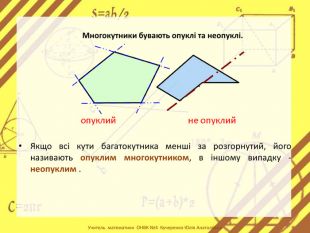
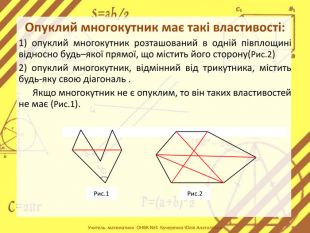
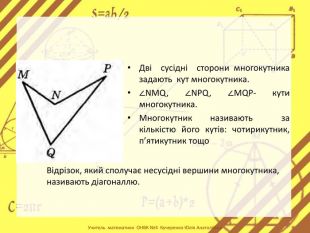
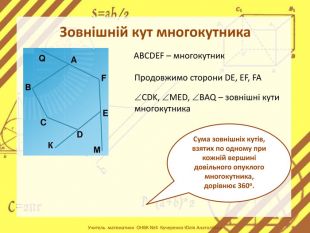
Мета:сформувати в учнів поняття многокутника та його елементів; периметра многокутника; опуклого многокутника; внутрішній та зовнішній кути многокутника; сума кутів опуклого п – кутника.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



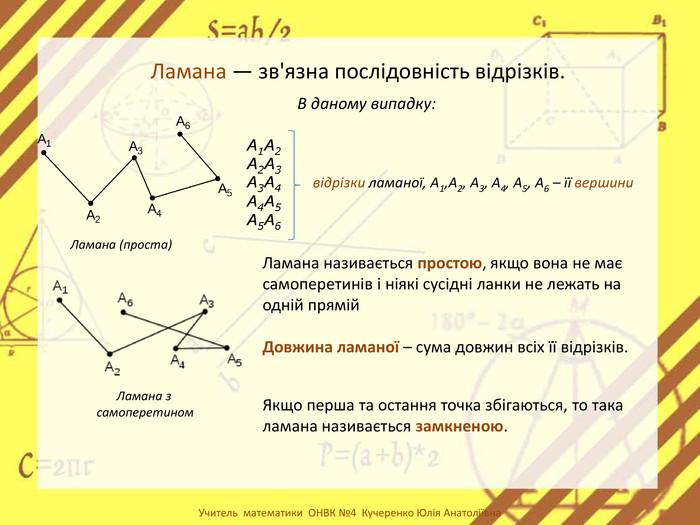

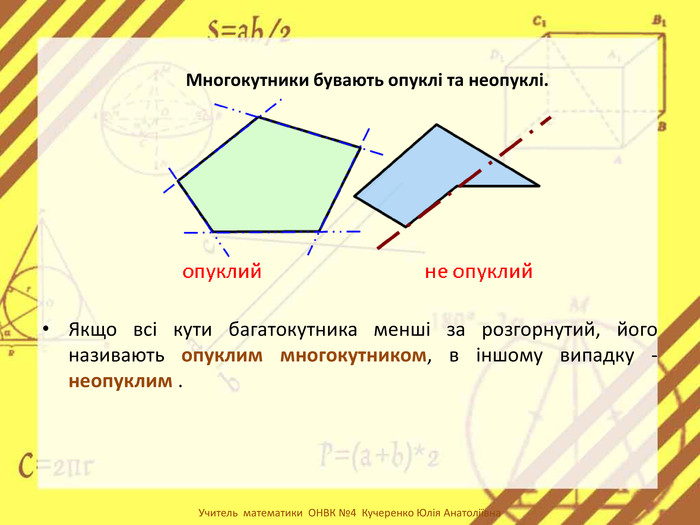
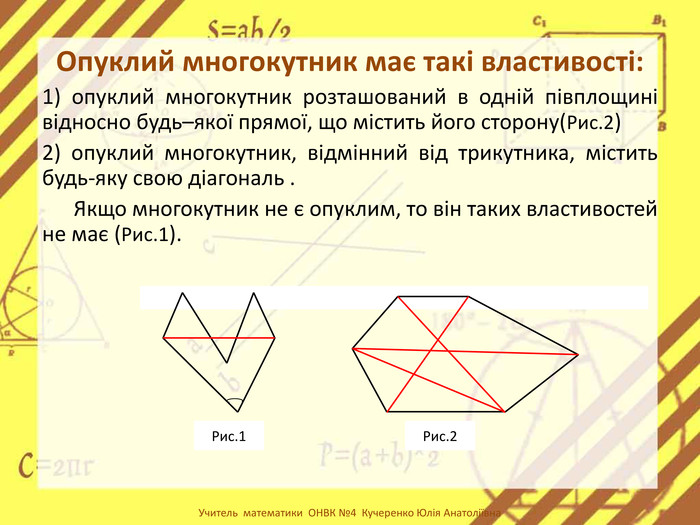
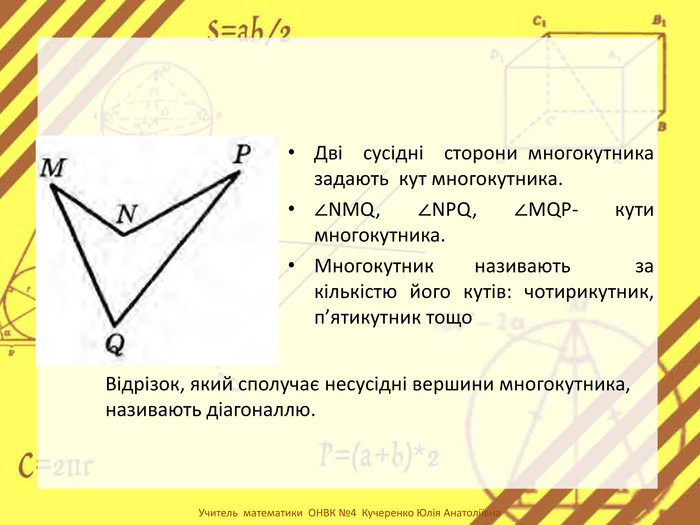

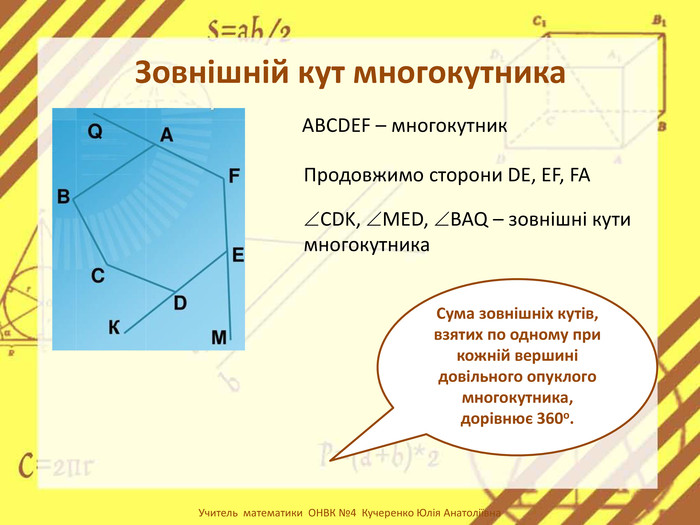
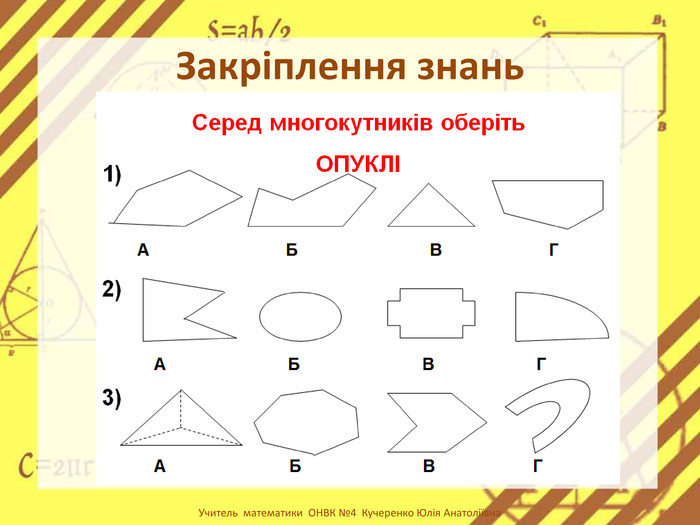
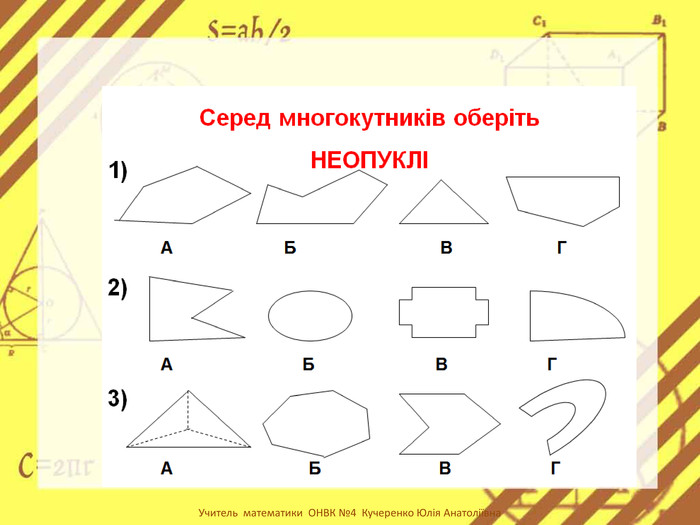




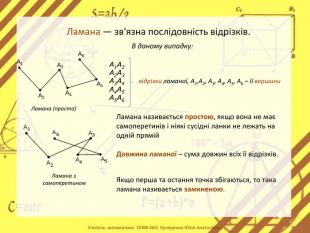





-

Телюпа Олена Анатолiiвна
12.03.2025 в 14:46
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Данилець Вікторія
03.03.2025 в 17:43
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Зінченко Валентина Сергіївна
12.03.2024 в 21:00
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Большак Ірина
08.03.2024 в 08:17
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Буриліна Інна В'ячеславівна
21.04.2023 в 00:25
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лебедева Юля
04.04.2023 в 09:09
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kr Elena
11.03.2023 в 17:01
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Брязкало Юлия
27.09.2022 в 11:47
Дуже сподобалась презентація! Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кравченко Лілія
11.04.2022 в 22:43
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Дзядевич Наталья
11.04.2022 в 14:04
Дякую! Стало у нагоді!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кушина Антоніна Василівна
01.03.2021 в 16:04
Дякую!!!!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 8 відгуків