План уроку:

1.   Поняттявекторау просторі

2.   Координативектора

3.   Модульвектора

4.   Колінеарнівектори

5.   Рівністьвекторів

6.   Додавання векторів. Віднімання векторів. Множення вектора на число

7.   Діїнад векторами,що заданікоординатами

8.   Скалярнийдобутоквекторів

9.   Кут між векторами

10.Умоваперпендикулярностівекторів

Поняття вектора у просторі

Вектором називається напрямлений відрізок

Кінець вектора вектор AB

Початок вектора

r вектор a

Координати вектора

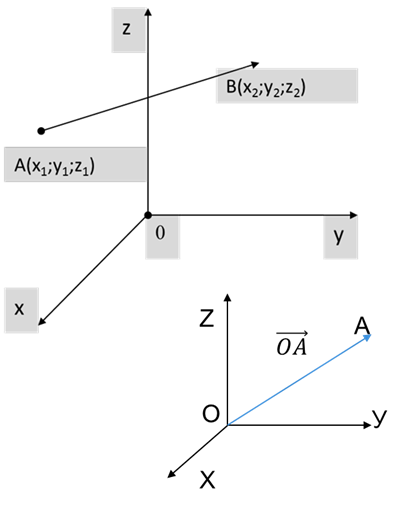
Координати вектора дорівнюють різниці координат його кінця та початку

ABx₂ x₁; y₂ y₁;z₂ z₁

Координати вектора, для якого початком є початок координат дорівнюють координатам його кінця

OAx_A; y_A;z_A

Нульовий вектор AA0

                  AA Будьвектор-яка точканазиваєтьсяплощининульовимє вектором. Початок.                                Такий

                                                      нульового вектора збігається з його кінцем.                                                     

Модуль вектора

Модуль вектора (абсолютна величина вектора) – довжина відрізка, що зображує вектор.

Довжина вектора АВ позначається так: 𝐴𝐵

AB  xAB2  yAB2 zAB2 a  x²  y² z²

Довжина нульового вектора дорівнює нулю

AA0

Колінеарні вектори

Ненульові вектори називаються колінеарними, якщо вони

лежать на одній прямій, або на паралельних прямих; нульовий вектор вважають колінеарним будь-якому вектору.

Умова коліанерності векторів:

  b¹ b² b³ ba  

a1 a2 a3

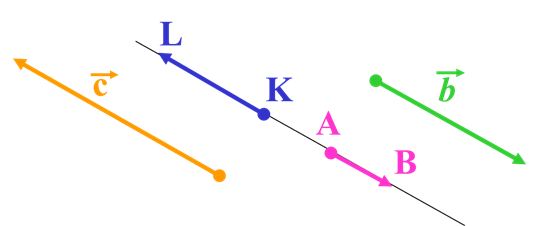
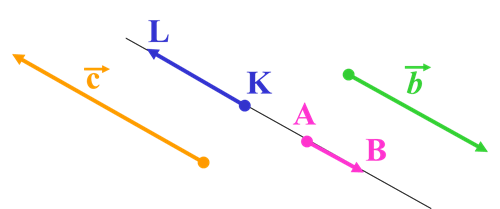
Колінеарні вектори, які мають однаковий напрям, називаються співнапрямленими векторами

cKL,  ABb

Колінеарні  вектори,    які мають різні  напрями, називаються    протилежно  напрямленими векторами.

cAB,   c b,  KLb,  ABKL

Рівність векторів

Вектори називаються рівними, якщо вони співнапрямлені і їх довжини рівні

Додавання векторів

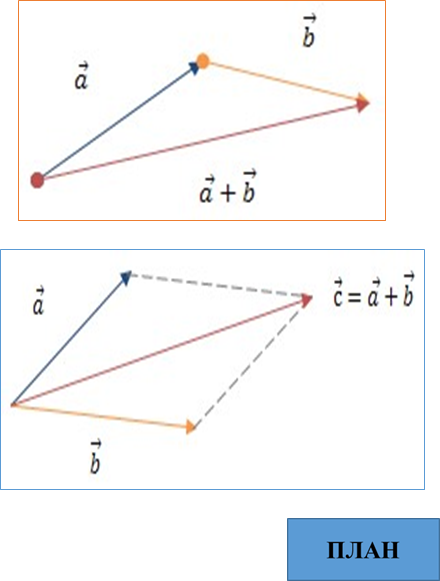Правило трикутника

Правило паралелограма

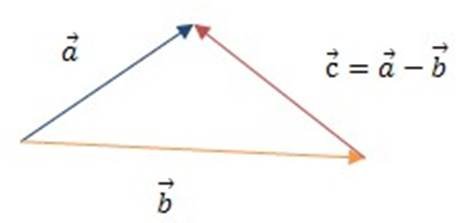
Віднімання векторів

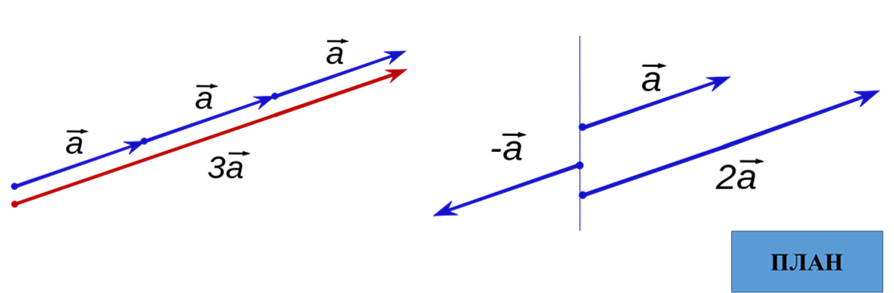
Множення вектора на число

Дії над векторами, що задані координатами

Додавання

ax_а; y_а;z_аbx_b; y_b;z_bx_a x_b; y_a  y_b;z_a z_b

Закони додавання:

Переставний abba

^{Сполучний}           (ab)сa(bc)

Віднімання

axa; ya;zabxb; yb;zbxa xb; ya yb;za zb

Множення вектора на число a  ^x_a;^y_a;^z_a

Скалярний добуток векторів

Скалярним добутком двох векторів називається число, яке дорівнює сумі добутків відповідних координат цих векторів.

Якщо вектори                                        , то  ax₁; y₁;z₁i bx₂; y₂;z₂

ab  x₁x₂  y₁y₂  z₁z₂

Скалярний квадрат вектора дорівнює квадрату його модуля

2 2 a  a

Скалярний добуток двох векторів дорівнює добутку довжин цих векторів на косинус кута між ними.

ab  a  b cos

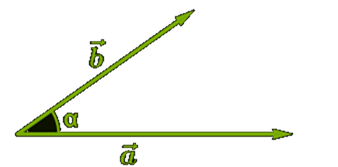
Кут між векторами

Кутом між векторами називається кут між векторами, рівними даним і такими, що мають спільний початок

ab

сos a  b

Якщо вектори співнапрямлені, то кут α=0⁰

Якщо вектори протилежно напрямлені, то α=180⁰

Кут між векторами

Уважно розглянемо випадки, коли вектори утворюють тупий кут:

Оскільки косинус тупого кута від’ємний, то скалярний добуток векторів, які утворюють тупий кут, є від’ємним.

Умова перпендикулярності векторів

Вектори називають перпендикулярними, якщо                                                                 a;b 90⁰

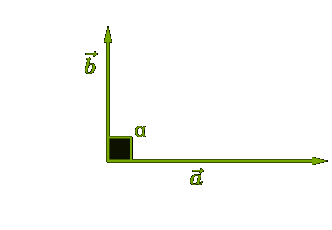
Оскільки cos 90⁰ = 0, то скалярний добуток перпендикулярних векторів дорівнює 0.

a  b  ab  0