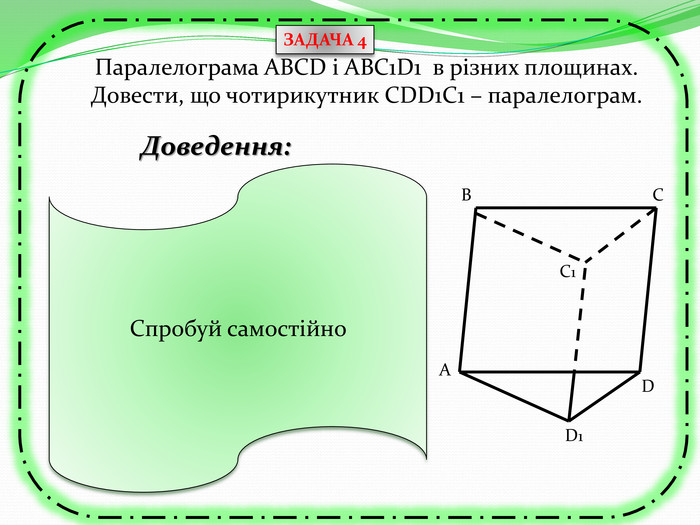
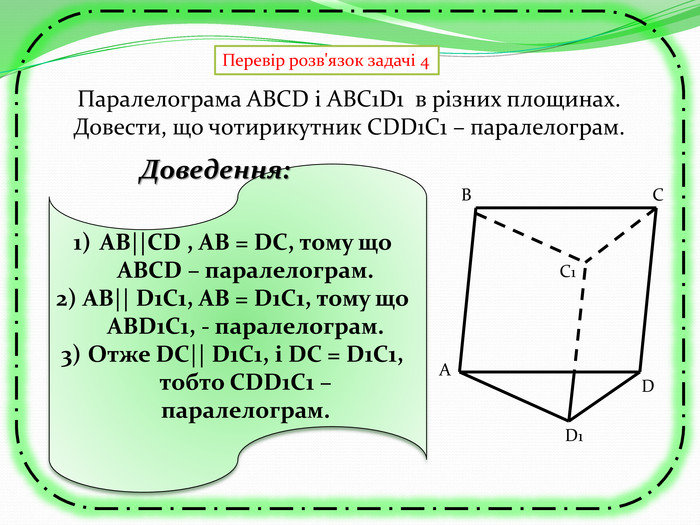
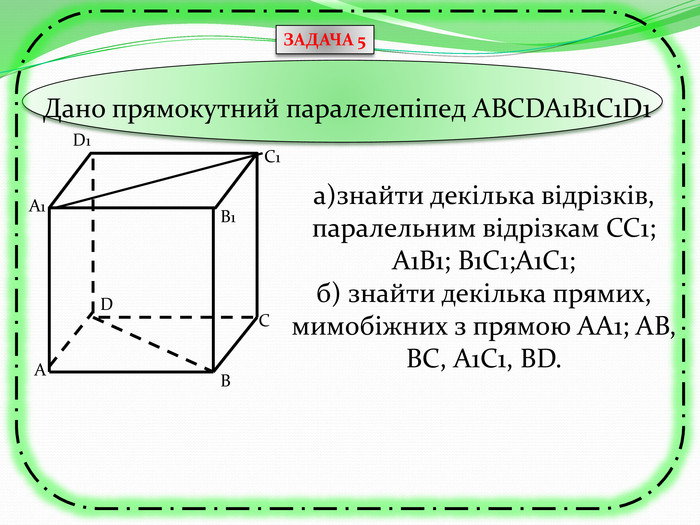
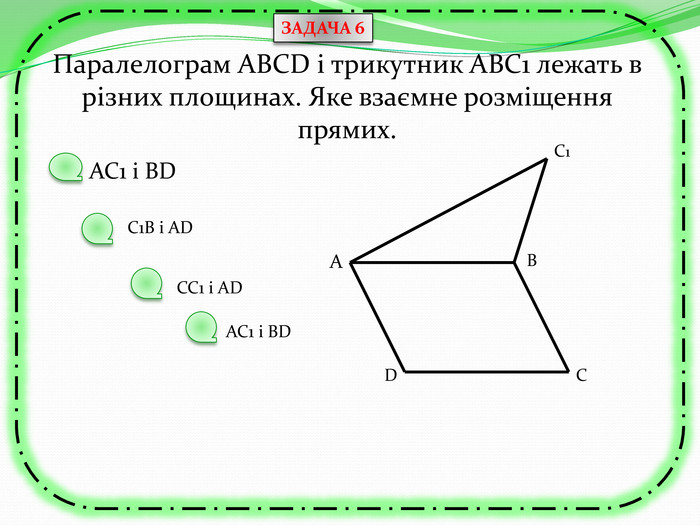
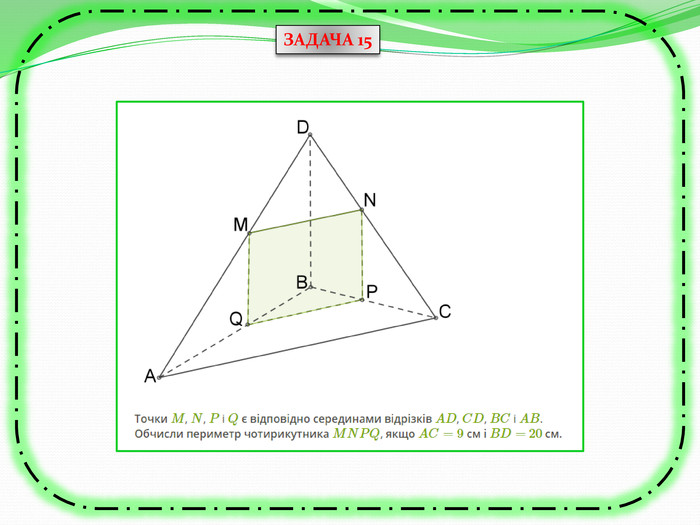
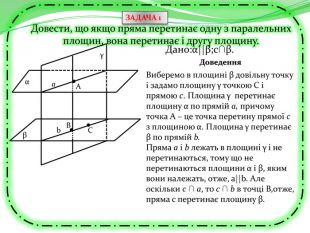
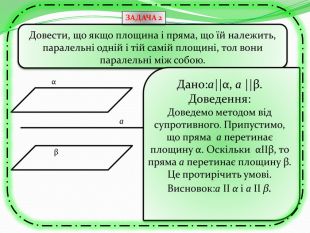
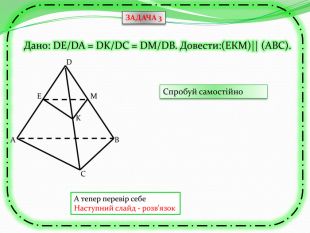
Презентація з теми "Паралельність прямих та площин в просторі. Тренувальні вправи"
Про матеріал
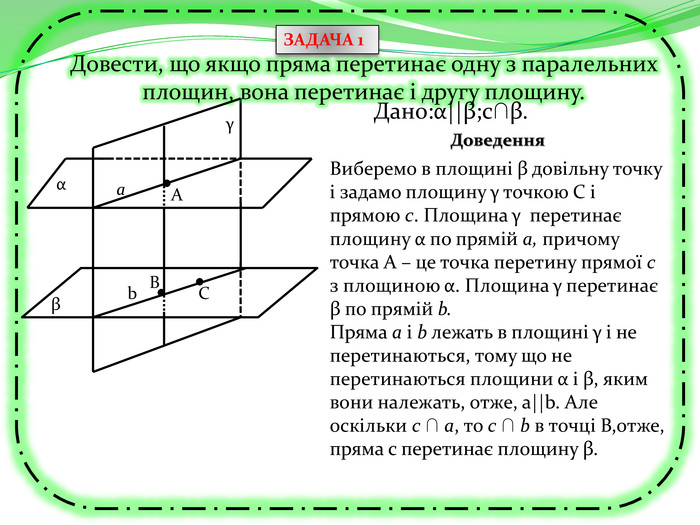
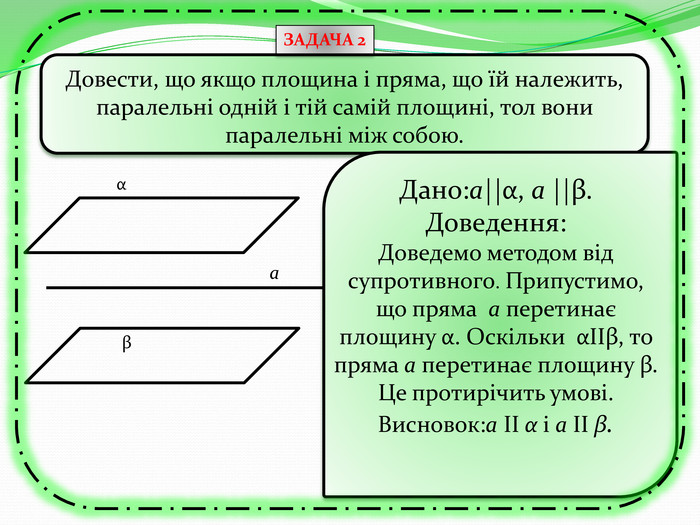
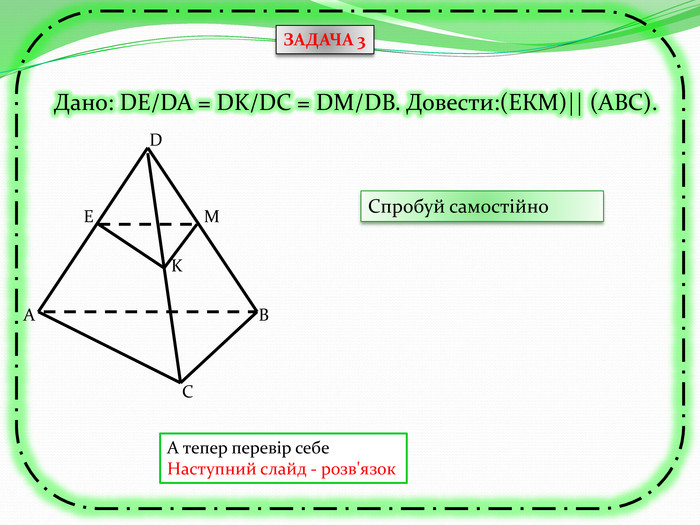
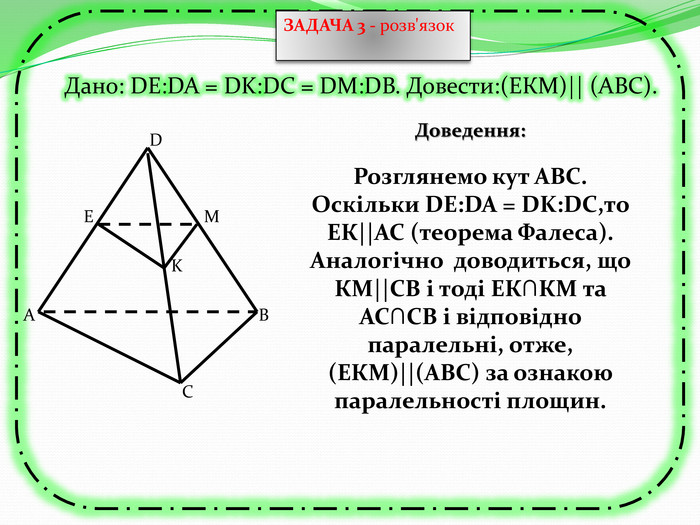
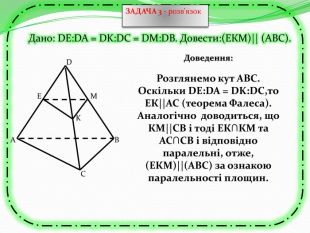
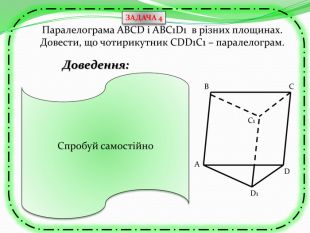
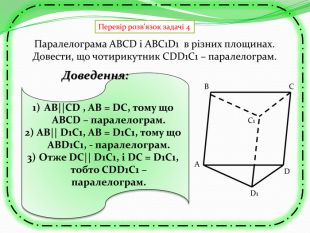
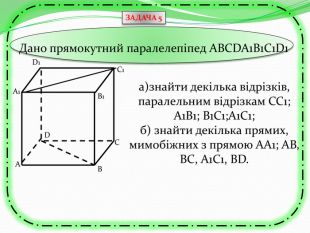
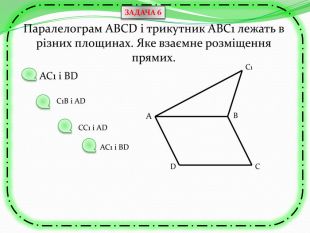
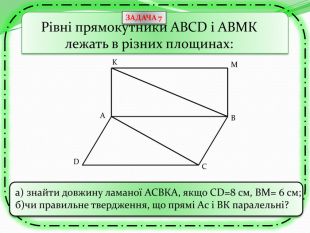
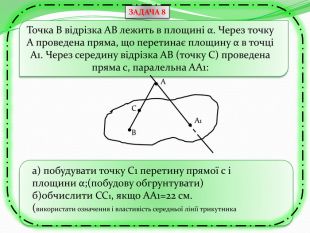
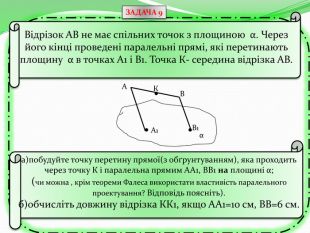
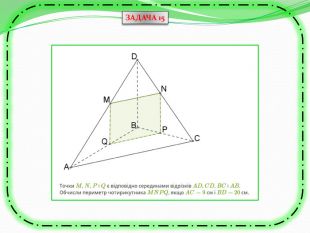
Презентація може бути використана як учителем на уроці для узагальнення знань, так і для самостійного роботи учнів при розв'язуванні вправ та задач, бо є вказівки та типові розв'язки задач з теми "Перпендикулярність прямих та площин в просторі. Тренувальні вправи" Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку