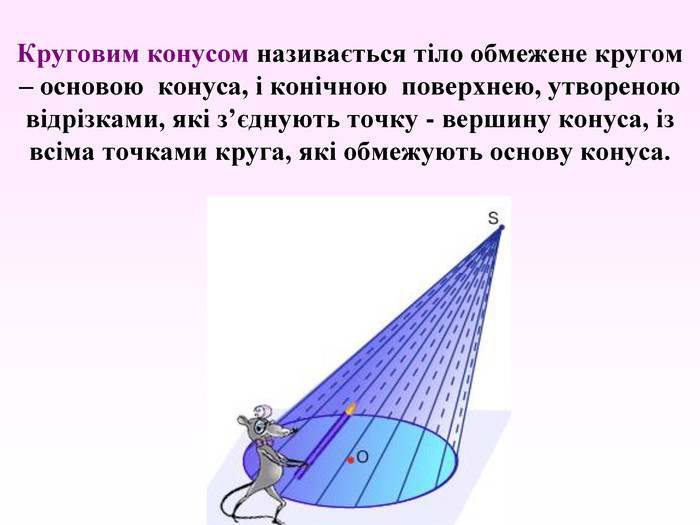
Презентація на тему "Конус"
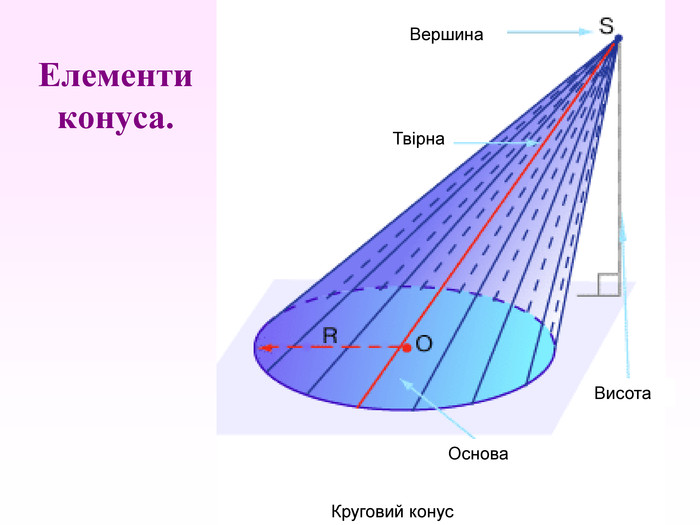
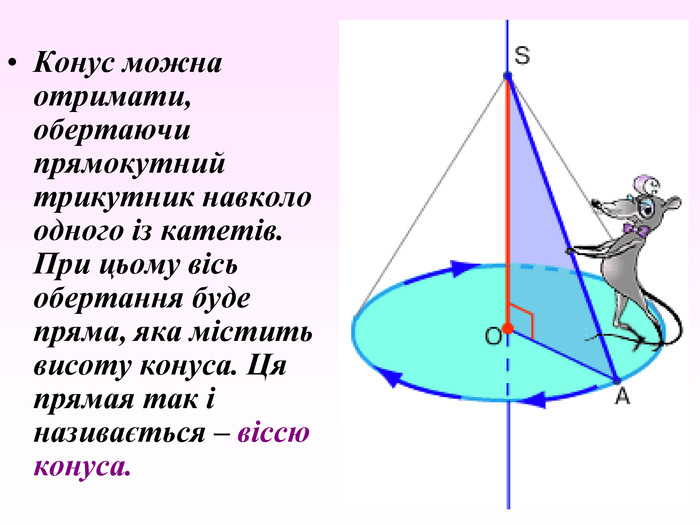
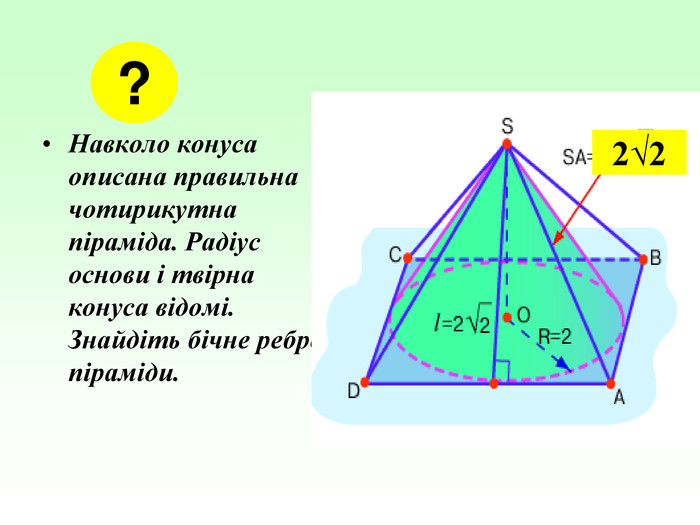
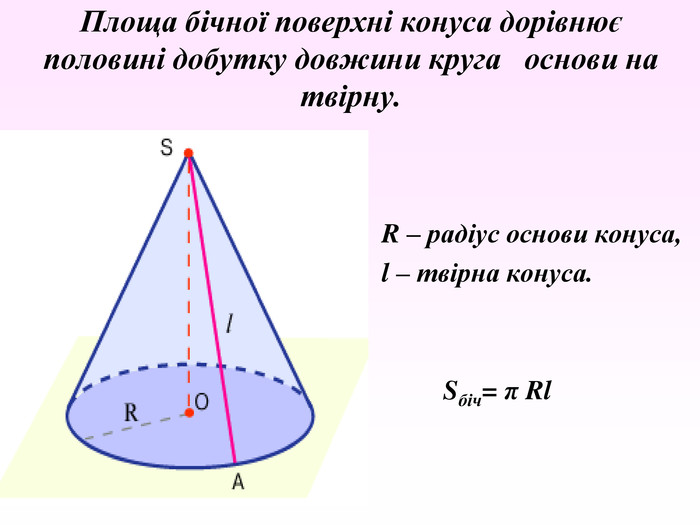
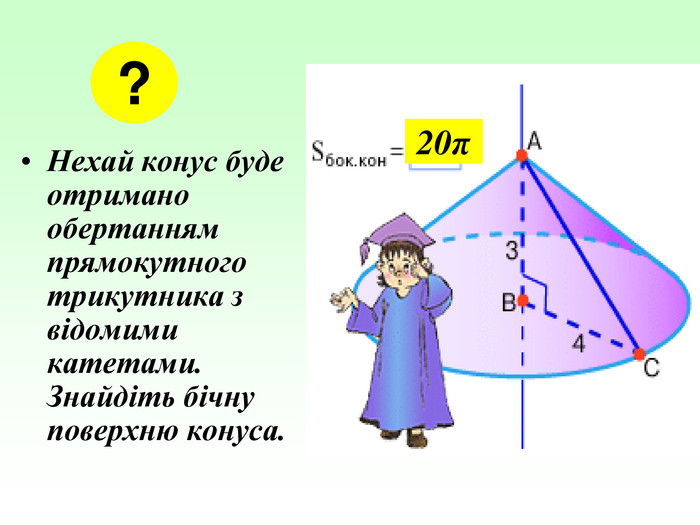
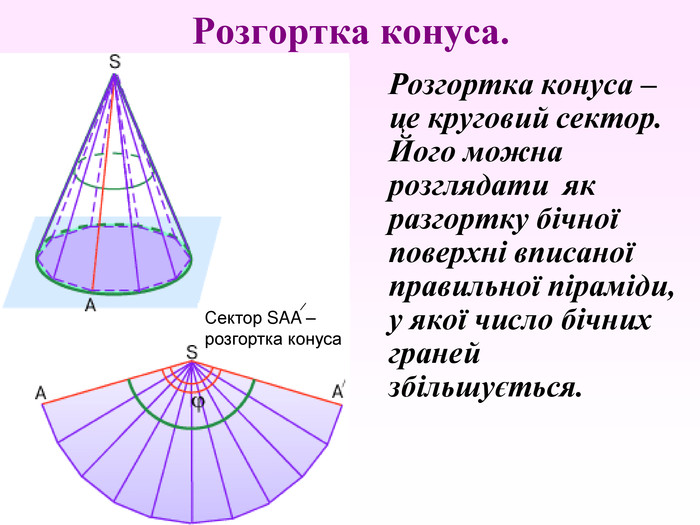
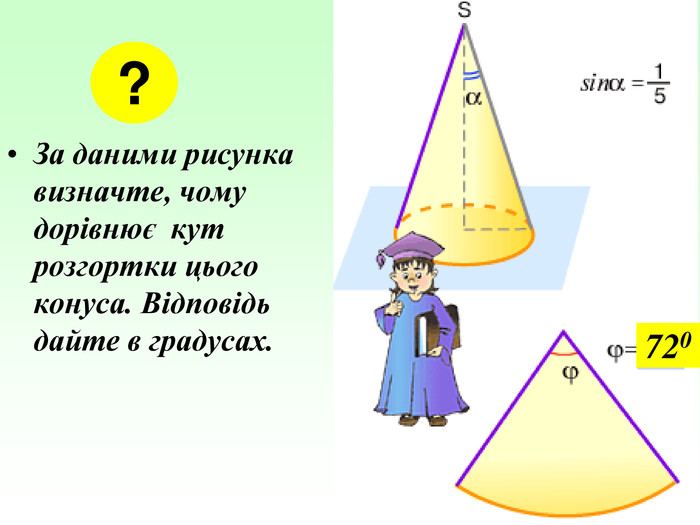
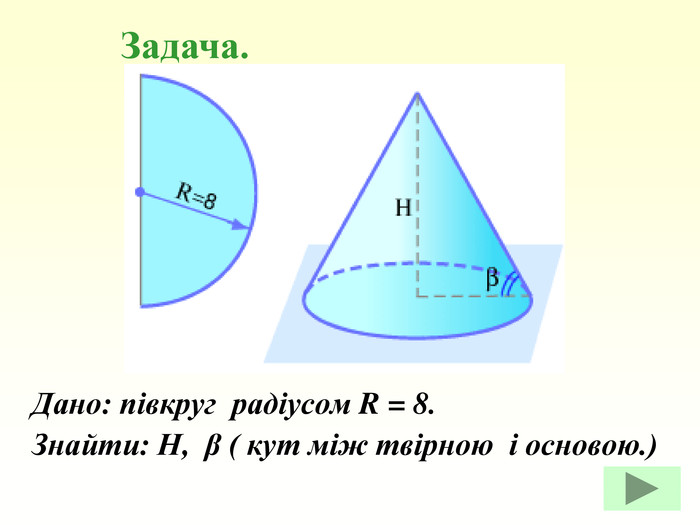
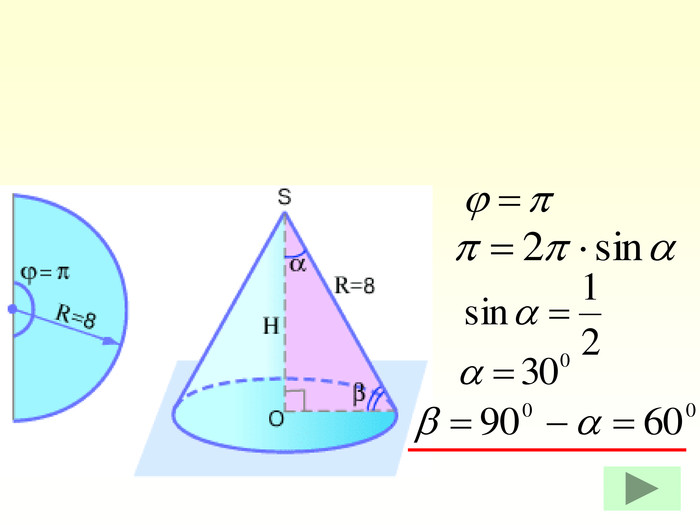
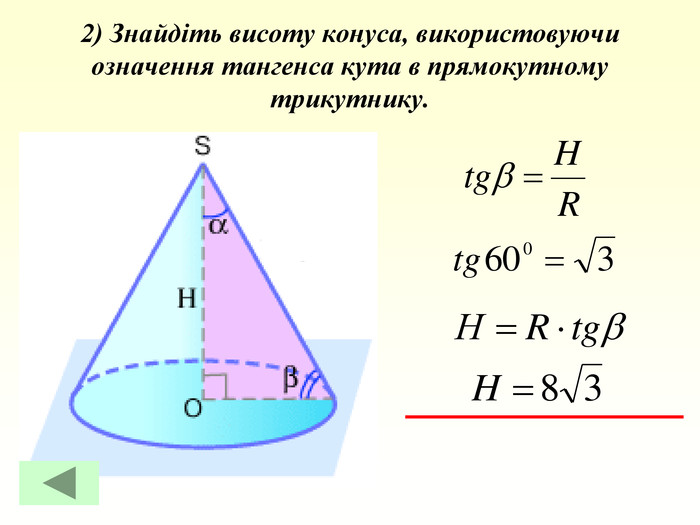
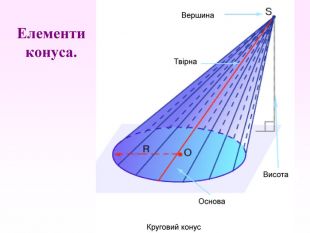
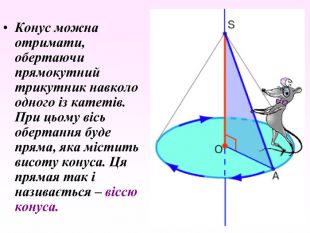
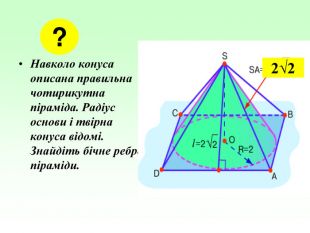
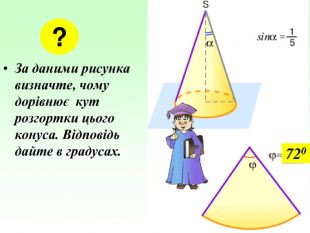
Конус — геометричне тіло , отримане шляхом об'єднання всіх променів, що виходять з однієї точки — вершина конуса, і таких що проходять через довільну плоску криву. Іноді конусом називають частину такого тіла, отриману об'єднанням усіх відрізків, що з'єднують вершину і точки пласкої поверхні (яку в такому випадку називають основою конуса, а конус називають таким, що спирається на дану поверхню). Надалі буде розглядатися саме цей випадок, якщо не сказано про інше.
Означення конуса.
Круговим конусом називається тіло обмежене кругом – основою конуса, і конічною поверхнею, утвореною відрізками, які з’єднують точку - вершину конуса, із всіма точками круга, які обмежують основу конуса.
Елементи конуса. Вершина Твірна Висота Основа Круговий конус
Прямий круговий конус. Круговий конус називається прямим, якщо його висота попадає в центр круга.
Всі твірні конуса рівні між собою і складають один кут з основою.
Чому дорівнює кут між твірною і основою конуса, якщо відомо кут між висотою і твірною. ? 650
Конус можна отримати, обертаючи прямокутний трикутник навколо одного із катетів. При цьому вісь обертання буде пряма, яка містить висоту конуса. Ця прямая так і називається – віссю конуса.
Конус утворено при обертанні прямокутного трикутника S = 14. Радіус основи конуса - 4. Знайдіть висоту цього конуса. ? 7
Вписана і описана піраміди. Пірамідою, вписаною в конус, називається така піраміда, основа якої – многокутник, вписаний в основу конуса, а вершина співпадає з вершиною конуса.
Піраміда називається описаною навколо конуса, якщо її основа – це многокутник, описаний навколо основи конуса, а вершина співпадає з вершиною конуса. Вписана і описана піраміди.
Навколо конуса описана правильна чотирикутна піраміда. Радіус основи і твірна конуса відомі. Знайдіть бічне ребро піраміди. ? 2√2
Площа бічної поверхні конуса дорівнює половині добутку довжини круга основи на твірну. R – радіус основи конуса, l – твірна конуса. Sбіч= π Rl
Нехай конус буде отримано обертанням прямокутного трикутника з відомими катетами. Знайдіть бічну поверхню конуса. ? 20π
Розгортка конуса. Розгортка конуса – це круговий сектор. Його можна розглядати як разгортку бічної поверхні вписаної правильної піраміди, у якої число бічних граней збільшується. Сектор SAA –розгортка конуса
За даними рисунка визначте, чому дорівнює кут розгортки цього конуса. Відповідь дайте в градусах. ? 720
Дано: півкруг радіусом R = 8. Знайти: Н, β ( кут між твірною і основою.) Задача.
2) Знайдіть висоту конуса, використовуючи означення тангенса кута в прямокутному трикутнику.
Конус в побуті
про публікацію авторської розробки
Додати розробку