Презентація на тему: "Розв'язування тригонометричних нерівностей з параметром"

Розв’язування тригонометричних нерівностей з параметром

При яких значеннях параметра а нерівність 𝒔𝒊𝒏^𝟔𝒙 +

𝒄𝒐𝒔^𝟔𝒙 + a sinx cosx ≥ 0 виконується для усіх значень х?

Розв’язування.

Спочатку доцільно спростити задану нерівність. Cкористаємось формулами: сума кубів двох виразів та синус подвійного кута. (𝑠𝑖𝑛²𝑥 + 𝑐𝑜𝑠²𝑥)³= 𝑠𝑖𝑛⁶𝑥 +  Отримаємо, що

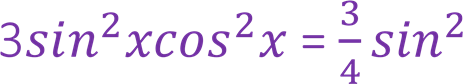2x.

Початкова нерівність приймає вигляд 

1 -3𝑠𝑖𝑛²𝑥𝑐𝑜𝑠²𝑥 + a sinx cosx ≥ 0 (1). Виконаємо заміну:

1 sinx cosx =t, t=. Таким чином, маємо квадратну

нерівність 3t²-at-1≤0 (2).Множиною значень функції sin 2x є

                 інтервал [- 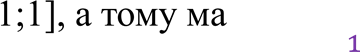       ємо подвійну нерівність

-.

Отже, треба знайти значення параметра а, такі при яких розв’язки нерівності (2) належать інтервалу [-0,5;0,5]. Ця умова виконується тільки у випадку, якщо f(t)= 3t²-at -1 приймає від’ємні, або нульові значення на кінцях проміжку.

Маємо f(-0,5)= 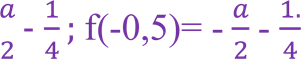 . Отже, треба розв’язати наступну систему нерівностей відносно параметра а.

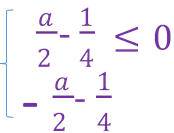
,     2a-1≤ 0,а≤ 0,5,    

                                                                                          ≤ 0;-2a-1≤ 0;      а≥ −0,5;                                          →- 0,5 ≤ а ≤ 0,5.

Відповідь: а ∈[- 0,5; 0,5].

Домашнє завдання.

При яких значеннях параметра а нерівність 𝒔𝒊𝒏^𝟒𝒙 + 𝒄𝒐𝒔^𝟒𝒙 − 𝟑 a sinx cos x > 0 виконується для усіх значень х?