Презентація на тему "Рух тіла під дією кількох сил (Розв'язування задач)"
Про матеріал
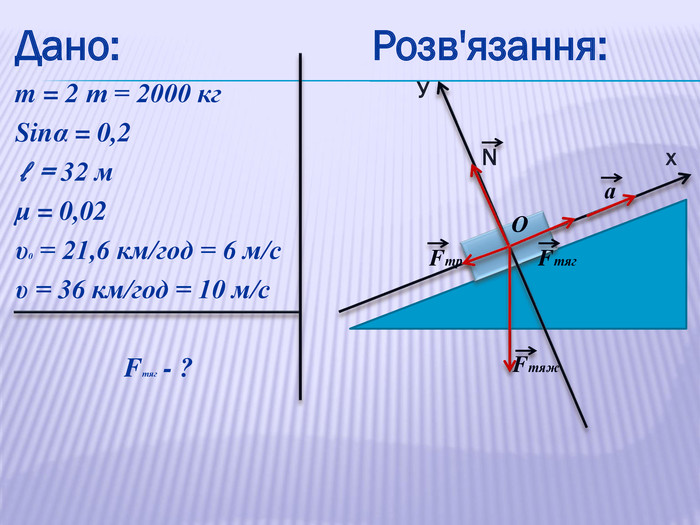
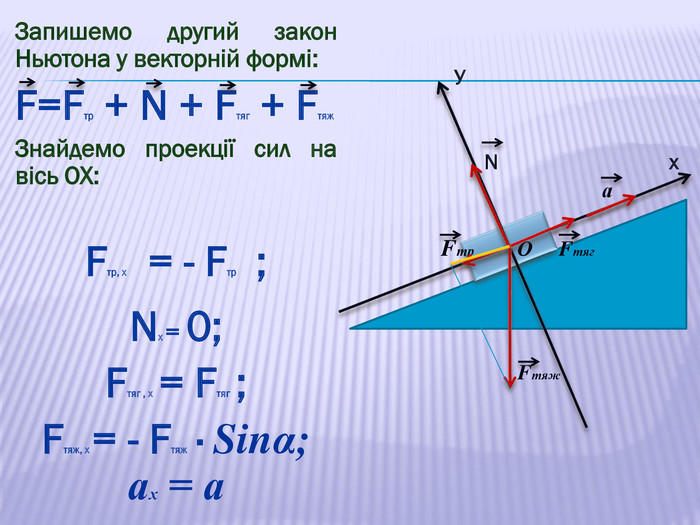
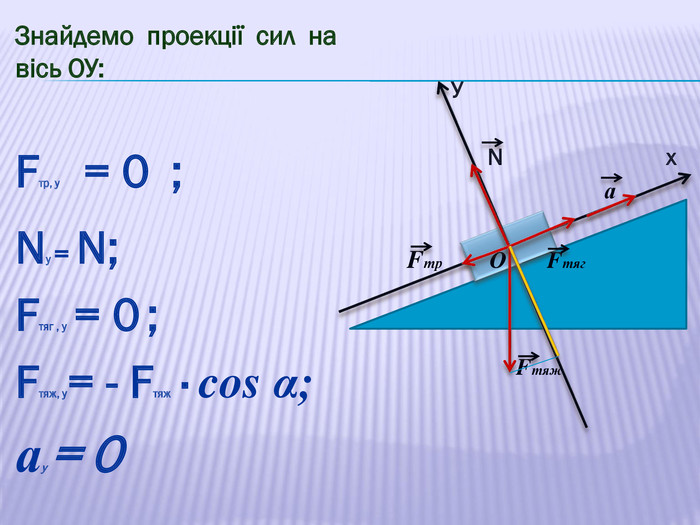
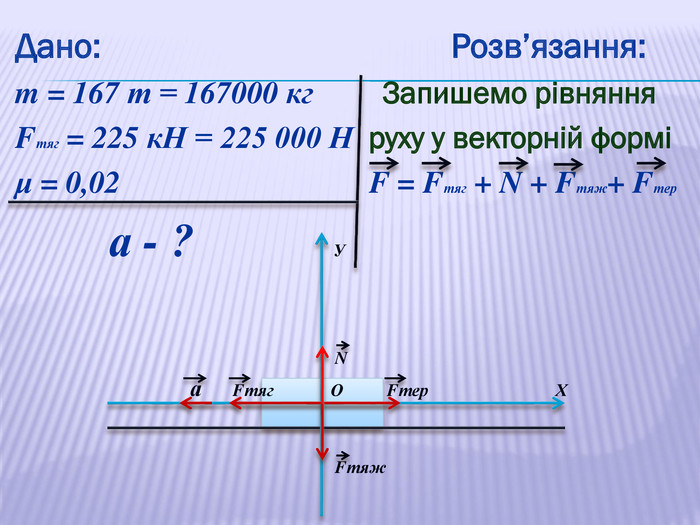
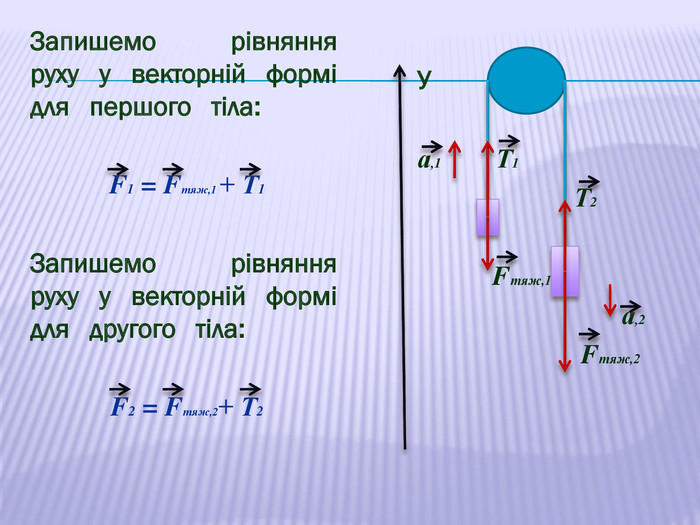
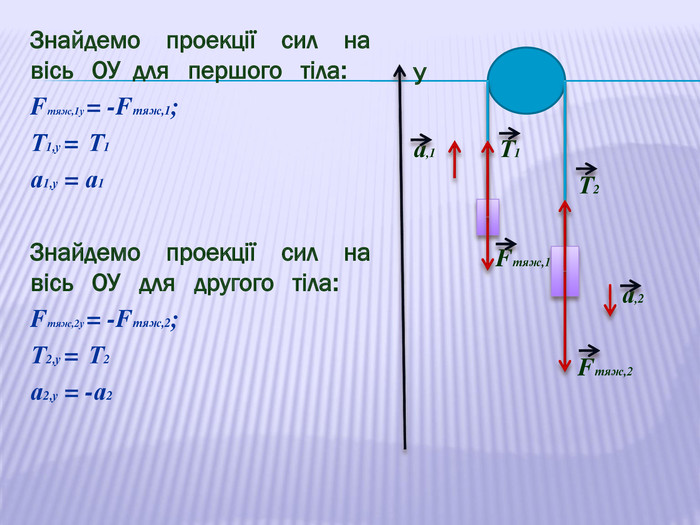
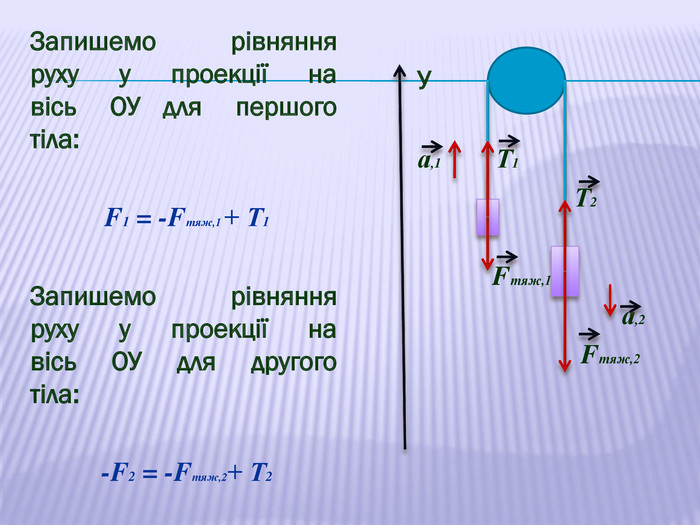
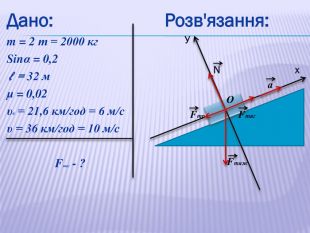
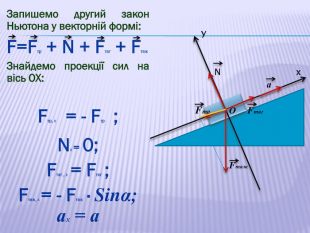
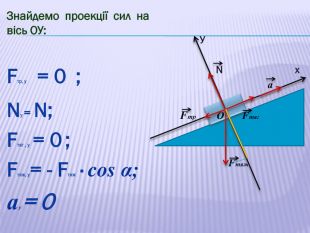
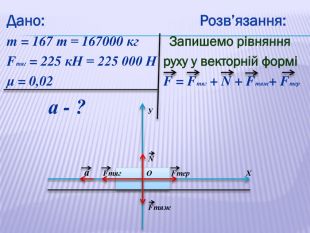
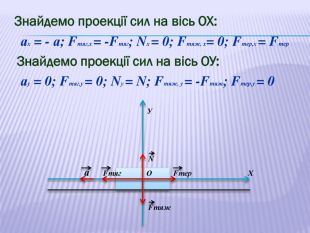
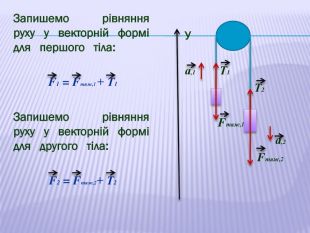
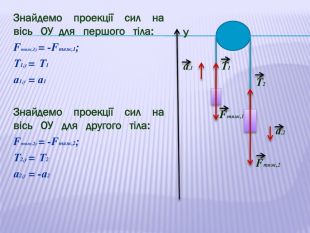
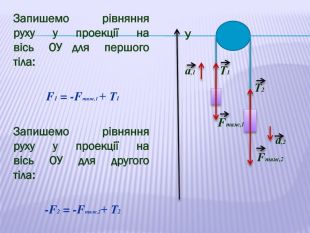
У презентації наведено приклади розв'язування задач про рух тіл під дією кількох сил: у горизонтальному напрямку, по похилій площині та рух зв'язаних тіл. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
























-

Бєлоусова Світлана Володимирівна
10.04.2024 в 01:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Рибенцева Альона Геннадіївна
14.03.2024 в 10:20
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Логойда Тетяна Василівна
07.04.2023 в 11:56
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Іменинник Людмила Миколаївна
16.03.2023 в 20:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гулич Руслан
16.03.2023 в 07:05
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Дворник Віктор
16.03.2023 в 06:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Дмитренко Таміла Миколаївна
04.04.2022 в 22:15
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Куценко Світлана Савівна
23.03.2022 в 11:07
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сікора Сергій Петрович
31.03.2021 в 11:36
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тонковид Ірина Юріївна
09.11.2020 в 15:32
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Доренська Наталія Антонівна
20.10.2020 в 01:43
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 8 відгуків