Презентація на тему "Системи рівнянь другого степеня" для учнів 9 класу
Про матеріал
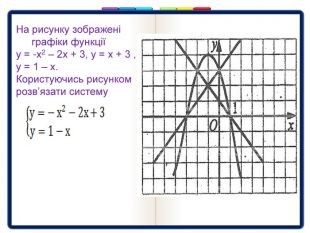
Дана презентація до уроку "Системи рівнянь другого степеня" дозволяє інтенсифікувати навчальний процес, активізувати пізнавальну діяльність, підвищити мотивацію учня до навчання, створити умови для підвищення ефективності уроку. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку