Презентація на тему: "Використання формул комбінаторики для обчислення ймовірностей подій"
Про матеріал
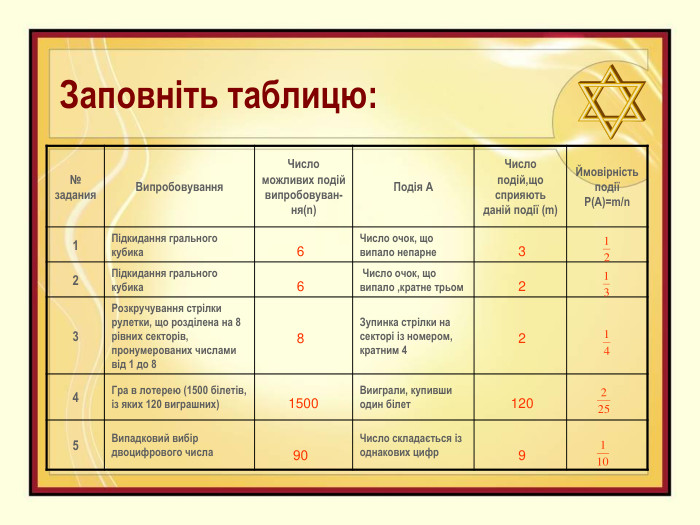
У розробці уроку розглянуті приклади розв'язання задач для обчислення ймовірностей випадкових подій із використанням формул комбінаторики. Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку