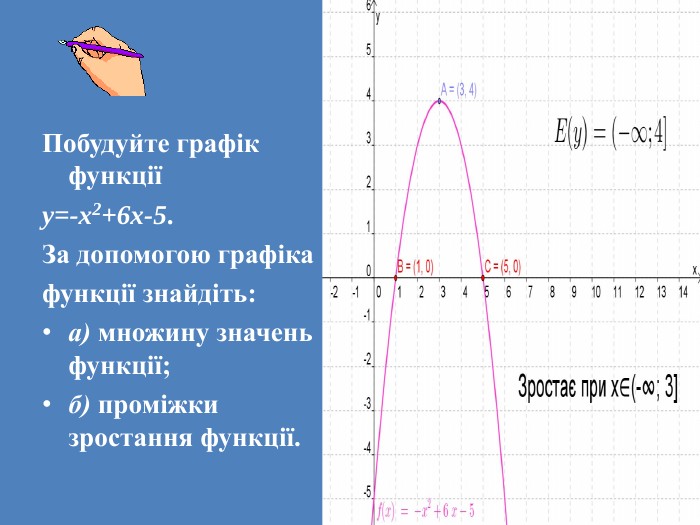
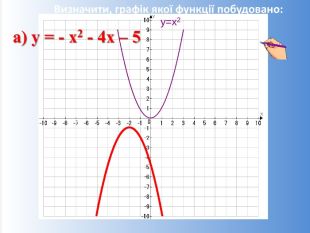
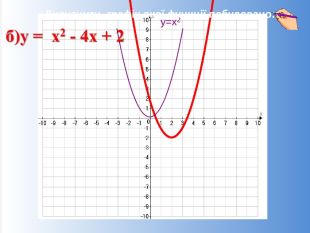
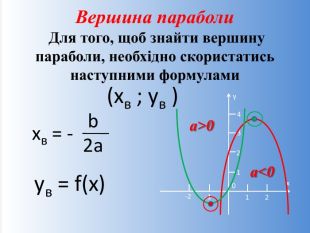
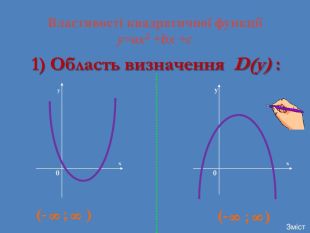
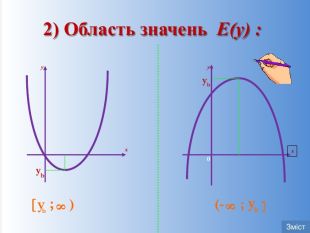
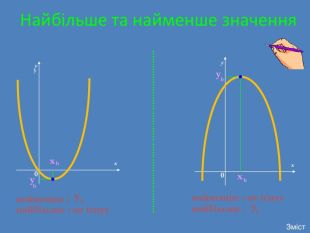
Презентація на урок алгебри у 9 класі з теми: "Квадратична функція та її властивості"
Про матеріал
Дану презентацію можна застосовувати на уроці алгебри у 9 класі при вивченні квадратичної функції Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра 9 клас (Прокопенко Н.С., Захарійченко Ю.О., Кінащук Н.Л.)
До уроку
РОЗДІЛ 2. КВАДРАТИЧНА ФУНКЦІЯ Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку





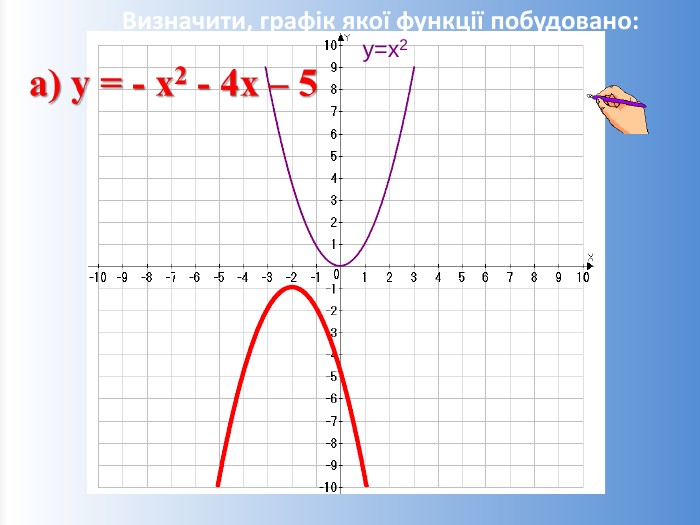
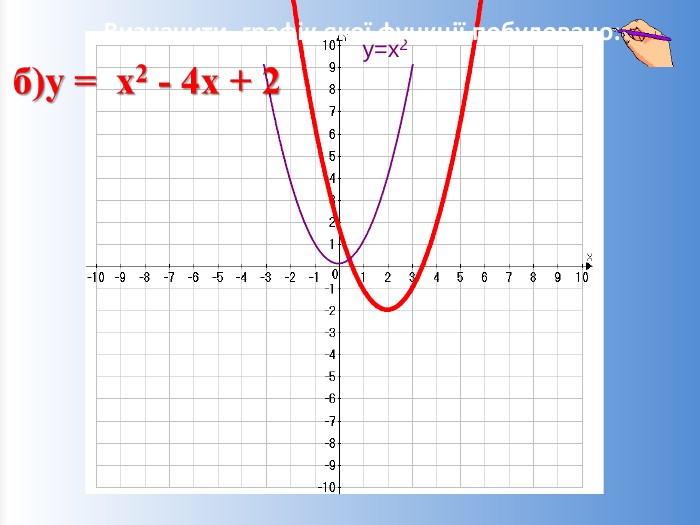




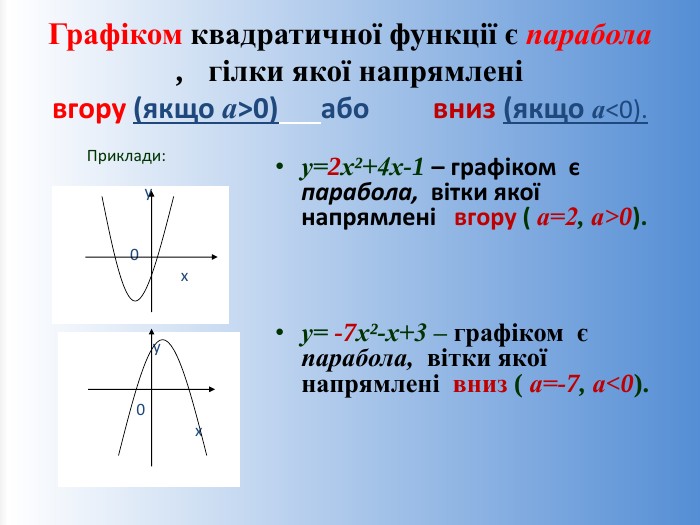


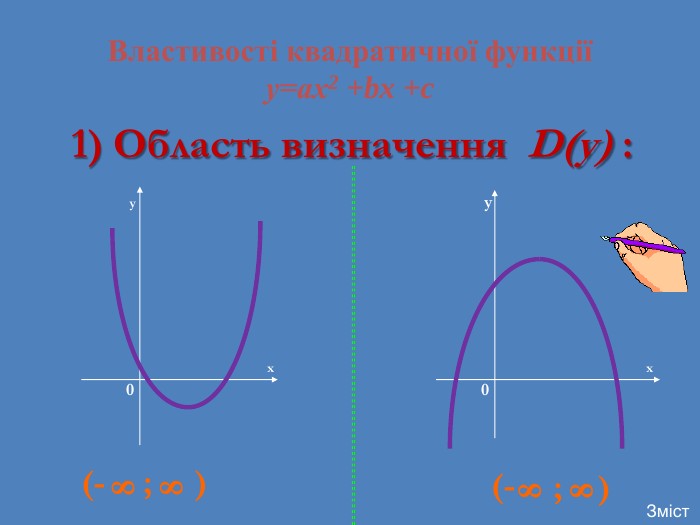
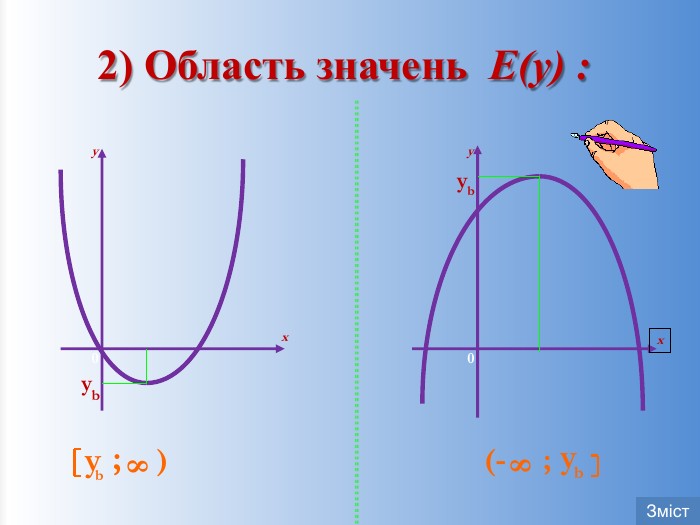
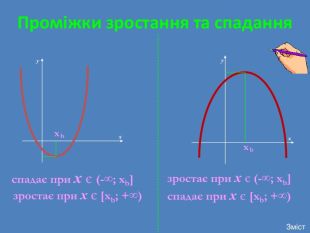
![Проміжки зростання та спаданняxxbbyyxxспадає при х є (-∞; хb]зростає при х є [xb; +∞)зростає при х є (-∞; хb]спадає при х є [xb; +∞)Зміст Проміжки зростання та спаданняxxbbyyxxспадає при х є (-∞; хb]зростає при х є [xb; +∞)зростає при х є (-∞; хb]спадає при х є [xb; +∞)Зміст](/uploads/files/4663/305125/331954_images/16.jpg)
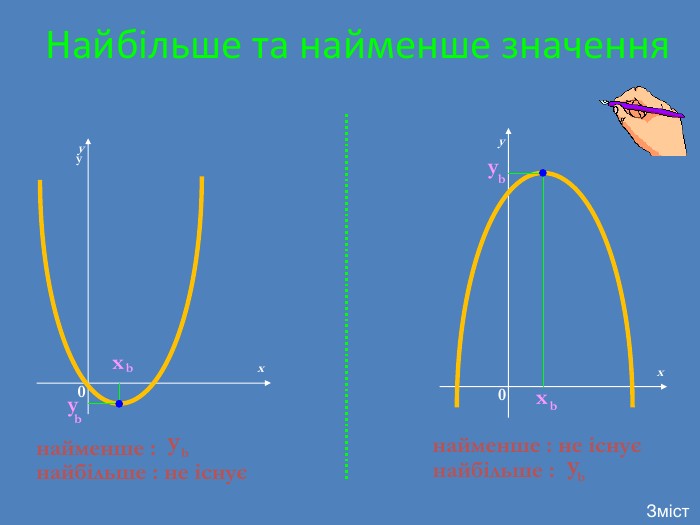

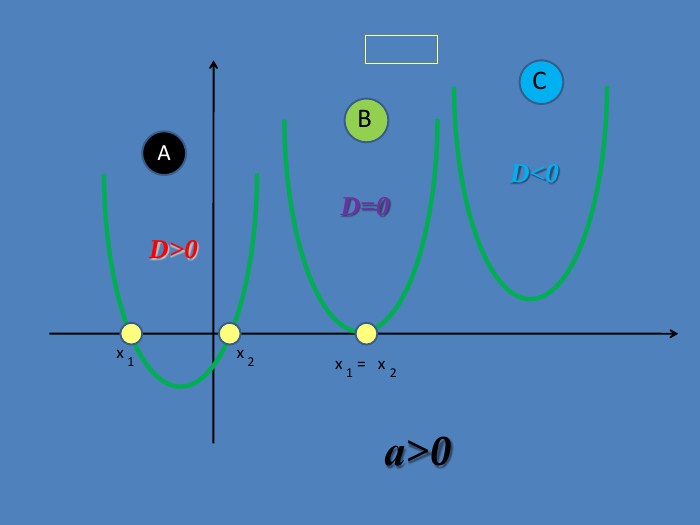

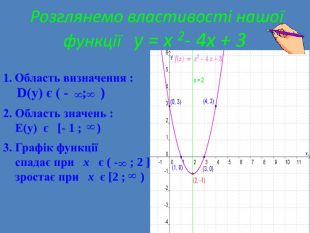
![Розглянемо властивості нашої функції y = x 2- 4x + 3 Область визначення : D(у) є ( - ; ) 882. Область значень : Е(у) є [- 1 ; )83. Графік функції спадає при x є ( - ; 2 ] зростає при x є [2 ; )88 Зміст Розглянемо властивості нашої функції y = x 2- 4x + 3 Область визначення : D(у) є ( - ; ) 882. Область значень : Е(у) є [- 1 ; )83. Графік функції спадає при x є ( - ; 2 ] зростає при x є [2 ; )88 Зміст](/uploads/files/4663/305125/331954_images/23.jpg)