Презентація Розв'язування систем лінійних нерівностей з однією змінною.

Іванюк Г. А. Тема уроку. Розв'язування систем лінійних нерівностей з однією змінною.

Розум полягає не лише в знаннях, але й у вмінні застосовувати ці знання. Аристотель. Епіграф уроку:

Усні вправи. При яких значеннях х дріб 1) визначений; 2) дорівнює нулю? Розв'яжіть нерівність:1) 2х > 4; 2) –х ≥ 3; 3) –x ≤ 0; 4) . Знайдіть переріз та об'єднання проміжків, що відповідають парі нерівностей:1) х ≥ 3 і ≥ 5; 2) х ≥ 3 і х ≤ 5; 3) х ≥ 5 і х ≤ 3.

Якщо доводиться знаходити спільні розв'язки двох або більшої кількості нерівностей з однією і тією самою змінною, то кажуть, що ці нерівності утворюють систему нерівностей. Систему нерівностей позначають фігурною дужкою:

Як знайти розв'язок системи нерівностей?Розв'язок системи нерівностей – це значення змінної, яке задовольняє кожну нерівність системи. Розв'язати систему нерівностей – означає знайти всі її розв'язки або показати, що вона їх немає.

Схема розв'язування систем лінійних нерівностей з однією змінною: Розв'язуємо кожну нерівність системи;Зображуємо множину розв'язків кожної нерівності на одній координатній прямій;Знаходимо переріз множини розв'язків нерівностей і записуємо множину розв'язків системи у вигляді проміжку або відповідної нерівності.

Приклад 1: Розв'яжемо систему нерівностей Розв'язок кожної з нерівностей системи є числовим проміжком, відповідно (3; +∞) і (-2; +∞). Запис (3; +∞)  (-2; +∞) означає переріз, тобто спільну частину даних проміжків. Розв'язком нерівності є проміжок (3; +∞).

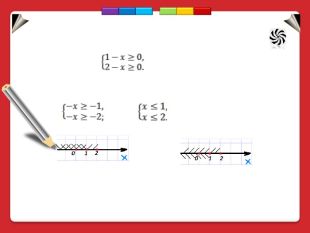
Приклад 2 Розв'язати систему нерівностей Розв'язання: або З рисунка видно, що розв'язком системи є х≤1, тобто х(-∞; 1]

Приклад 3 Розв'язати систему нерівностей Розв'язання: Очевидно, що числові проміжки (-∞; 5) і (6; ∞) не мають жодного спільного числа. Тому система нерівностей не має розв'язку. У такому випадку кажуть, що переріз даних числових проміжків – порожня множина, яку позначають знаком .

Усні вправи. Чи є числа: -4; 0; 5 — розв'язками: системи (№159)На рисунках позначено множини розв'язків нерівностей сис­теми. Чи є правильним запис множини розв'язків системи? (№160)

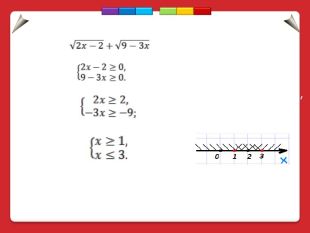
Приклад. Знайти область допустимих значень змінної у виразі Розв'язання: Аби даний вираз мав смисл, треба, щоб підкореневі вирази були невід'ємними: 2х – 2 ≥ 0 і 9 - 3х ≥ 0. Оскільки ця умова повинна виконуватися одночасно, то маємо систему: Розв'яжемо її. Бачимо, що спільні розв'язки нерівностей системи належать числовому проміжку [1; 3], який можна записати у вигляді подвійної нерівності 1≤х≤3.

Письмові вправи

Контрольні запитання. Що означає «розв'язати систему нерівностей»? Опишіть дії, які треба виконати, щоб отримати розв'язок системи нерівно­стей. Дано систему При яких а розв'язком системи є про­міжок: 1) (3; +∞); 2) (4; +∞): 3) (3; 4)?Дано систему: При яких а система має розв'язок:1) [2; 3]; 2) розв'язків немає; 3) х = 5?

1. ЩО ВАМ СПОДОБАЛОСЯ НА УРОЦІ?2. ЯКІ ЗАВДАННЯ ВИЯВИЛИСЯ ДЛЯ ВАС СКЛАДНИМИ?3. НАД ЧИМ ВАМ ПОТРІБНО ПОПРАЦЮВАТИ?