Презентація на урок геометрії в 11 класі на тему "Тіла обертання"
Про матеріал
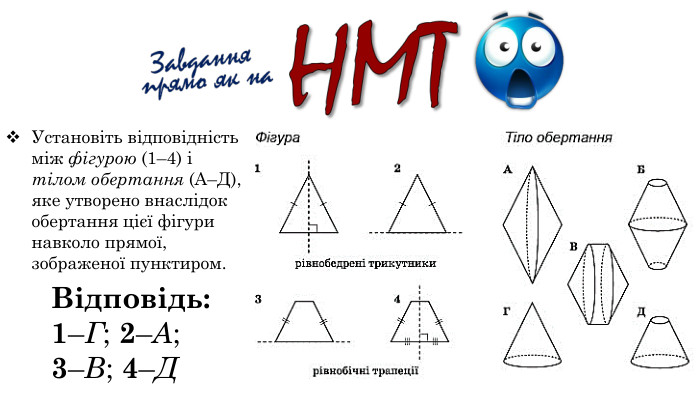
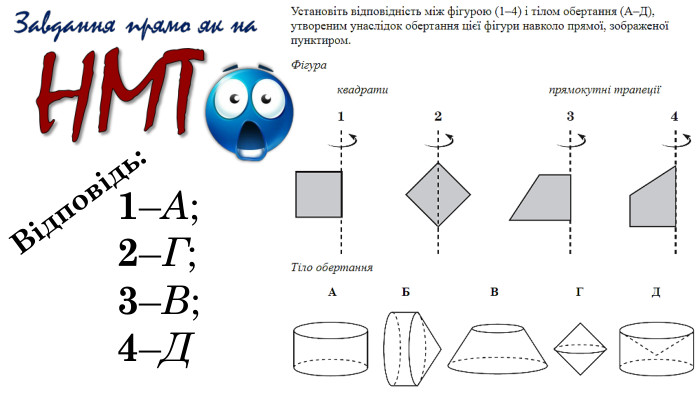
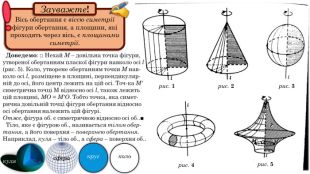
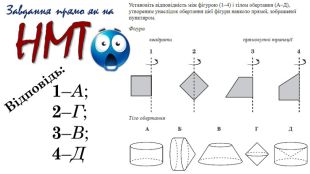
Містить ілюстрації, анімовані зображення для кращого розуміння матеріалу, визначення основних понять теми, рубрики "Історична довідка" та "Геометричні цікавинки", усні та письмові вправи та задачі й відповіді до них, рубрику "Завдання прямо як на НМТ" (у якій, відповідно, подані завдання зі ЗНО минулих років (2010, 2013, 2017) з теми "Тіла обертання"), а також узагальнення.
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку