Презентація "Навчальна діяльність на уроках математики"

Навчальна діяльність на уроках математики у контексті розвивального навчання

«Педагогіка повинна орієнтуватися не на вчорашній, а на завтрашній день дитячого розвитку… Навчання лише тоді ефективне, коли воно йде попереду розвитку»Л. С. Виготський

У 60–80 рр. колективом вчителів під керівництвом психологів Даниїла Борисовича Ельконіна і Василя Васильовича Давидова був закладений фундамент концепції розвивального навчання

Автори концепції свідомо орієнтувалися на фундаментальну людську здатність самостійно будувати і трансформувати особисту життєдіяльність, бути ії справжнім суб'єктом

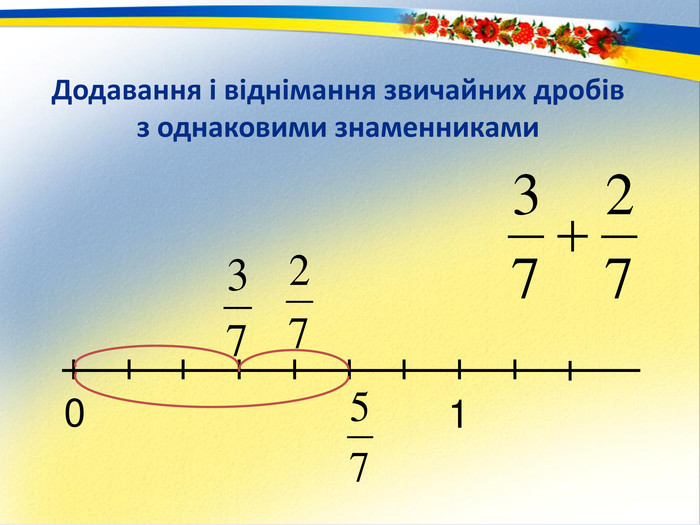
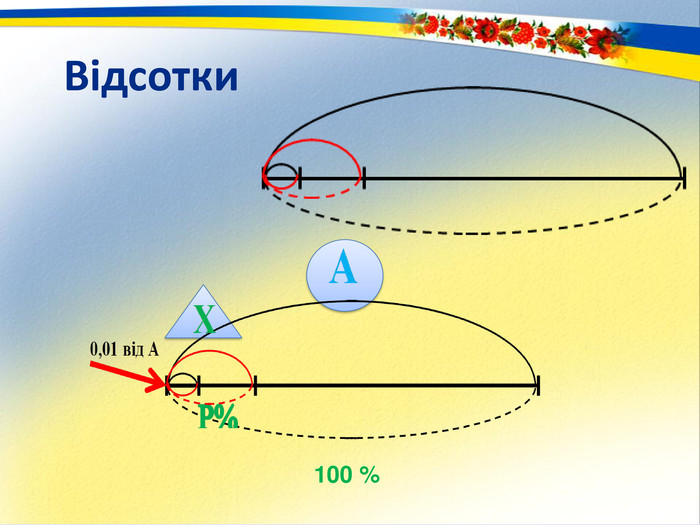
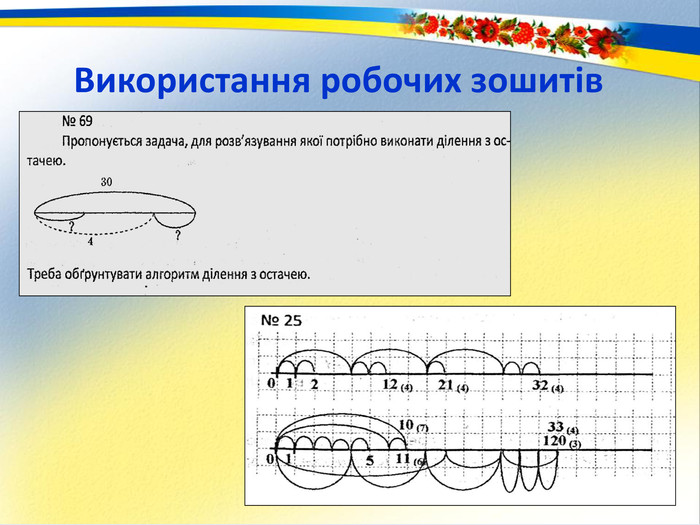
Своєрідність навчальної діяльності школярів Д. Ельконін вбачав не у засвоєнні знань і вмінь, а в самозміні дитини. При цьому школяр свідомо сприймає навчальну діяльність як особливу діяльність, як особисту мету. Пошуково-дослідницький метод —метод залучення учнів до самостійних і безпосередніх спостережень. Внесення елементу дослідження в навчальну діяльність.

У 1988 році почався етап активної практичної реалізації. Ця робота проводилася без урядової підтримки, але викликала жвавий інтерес у вчителів та батьків. З 1990 року кількість класів, які навчалися за новою системою, нараховувала декілька сотень, а потім і тисяч. У 1993 році система розвивального навчання була офіційно визнана в якості однієї з систем навчання.

У ЗОШ І–ІІІ ст. № 8 м. Житомира система розвивального навчання почала впроваджуватися з 1993 року З 2011 року систему РН почали впроваджувати у середній ланці. Згідно наукових досліджень достатньо працювати за цією системою з двох предметів (украінська мова та математика). Саме за ними працюємо наразі.

ЗАТВЕРДЖЕНОнаказом Міністерства освіти і науки України від 20.04.2018 № 405 Типова освітня програма закладів загальної середньої освіти ІІ ступеня Необхідною умовою формування компетентностей є діяльнісна спрямованість навчання, яка передбачає постійне включення учнів до різних видів педагогічно доцільної активної навчально-пізнавальної діяльності, а також практична його спрямованість. В. В. Давидов про навчальну діяльність: «Система РН полягає в тому, що безпосередньою основою розвитку школярів у процесі навчання є навчальна діяльність»

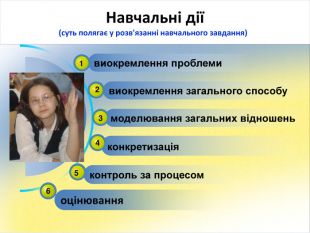
Система розвивального навчання розкриває широкі можливості для становлення самооцінки учня, допомагає йому усвідомити себе як суб'єкта, який саморозвивається, самостійно здобуває знання. Навчальна діяльність потребує рефлексії-оцінки щодо того ким учень був і ким став, яких результатів і завдяки чому досягнув, які труднощі відчуває і як їх подолати.

Структура навчальної діяльностінавчальні діїнавчальне завданняоцінювання 123навчально-пізнавальні мотиви 4

Навчальні дії (суть полягає у розв'язанні навчального завдання)  моделювання загальних відношень виокремлення загального способу виокремлення проблеми конкретизація контроль за процесом 123456

Педагог формує методику навчання згідно з трьома принципами: Від загального до конкретно визначеного (спочатку засвоюємо загальні правила розв’язання, потім застосовуємо до конкретного випадку);Знання нікому не даються в готовому вигляді;Навчання будується як пошук засобів для вирішення задач. Тому думка учня, яка відрізняється від загальноприйнятої, розглядається не як помилка, а як спроба мислити.

Яким має бути урок розвивального навчання?«Урок є відкриттям істини, пошуком істини, осмисленням істини в спільній діяльності вчителя та учня»

У такому навчанні вчитель виступає не лише джерелом інформації чи пояснення нового. Він повинен вміло поставити навчальну пізнавальну задачу. Вчитель – партнер, порадник, наставник. Майстерність вчителя полягає у вмінні висвітлити розумову діяльність учнів, а не власну ерудицію

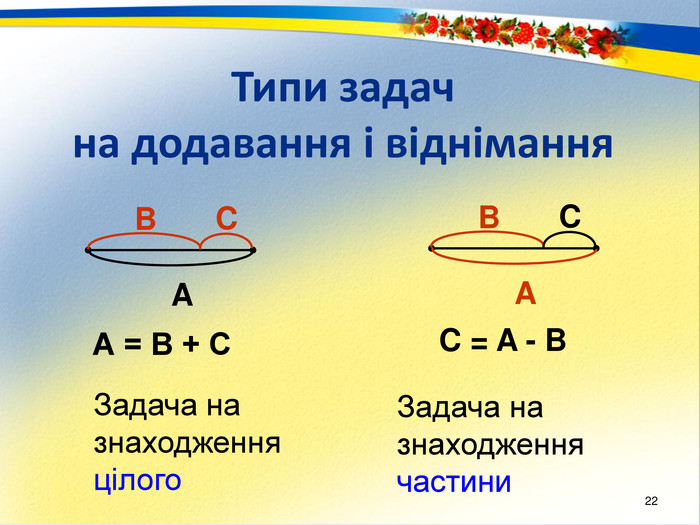
Провідна одиниця взаємодії учнів та вчителя у розвивальному навчанні – навчальна ЗАДАЧА. Весь навчальний процес розвивального навчання складається з вирішення навчальних задач, тобто навмисно спроектованих ситуацій, у яких учні в спільному пошуку знаходять поняття й конструюють на його основі узагальнений спосіб практичних дій.

Типологія уроків адекватна структурі навчальної діяльності: Урок постановки навчального завдання;Урок моделювання;Урок контролю;Урок оцінки дій.

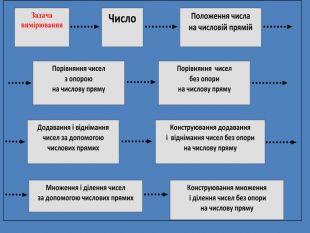
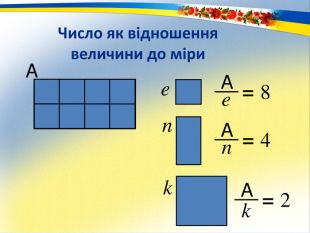
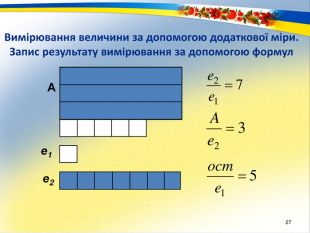
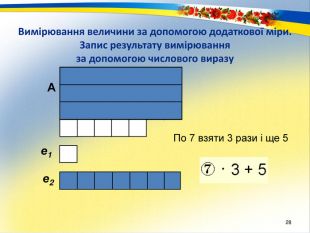
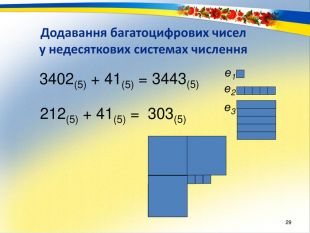
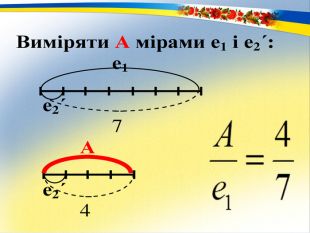
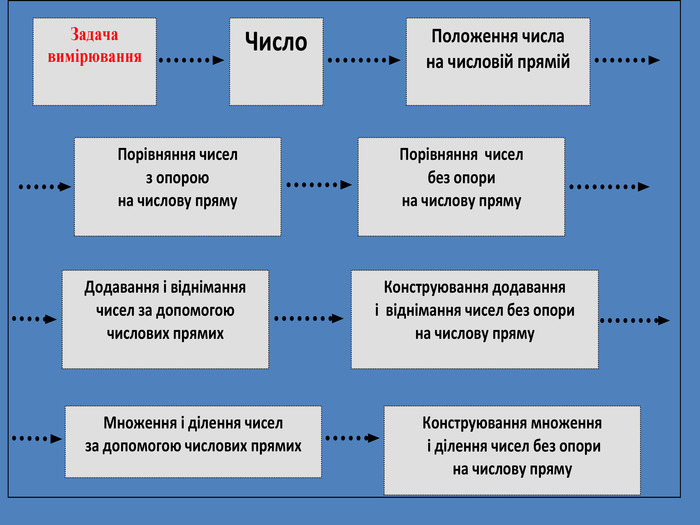
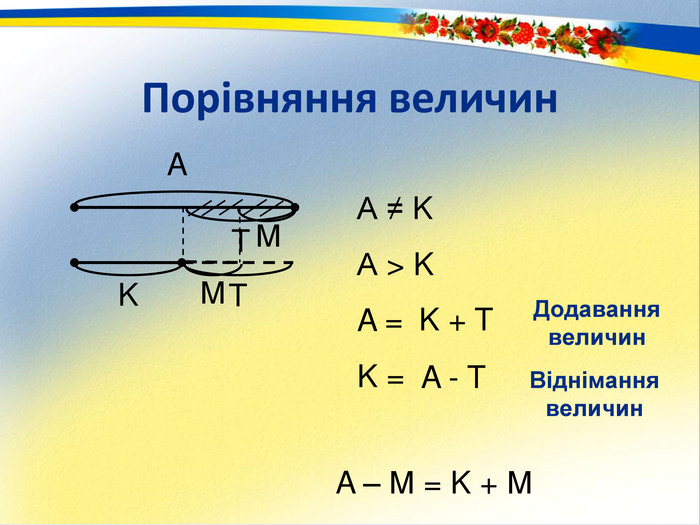
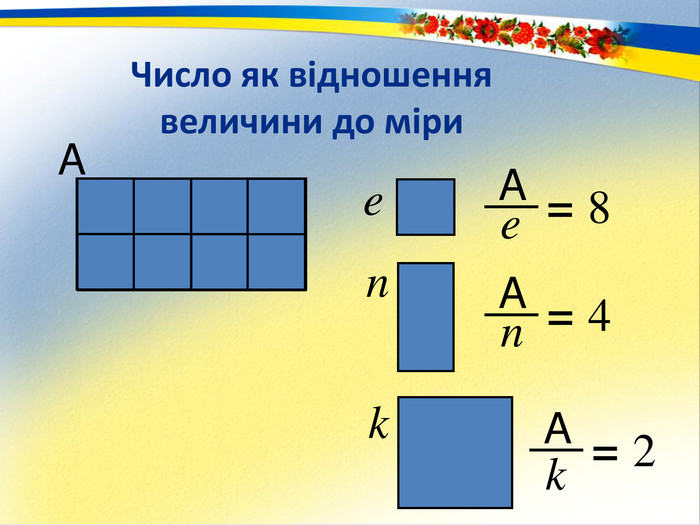
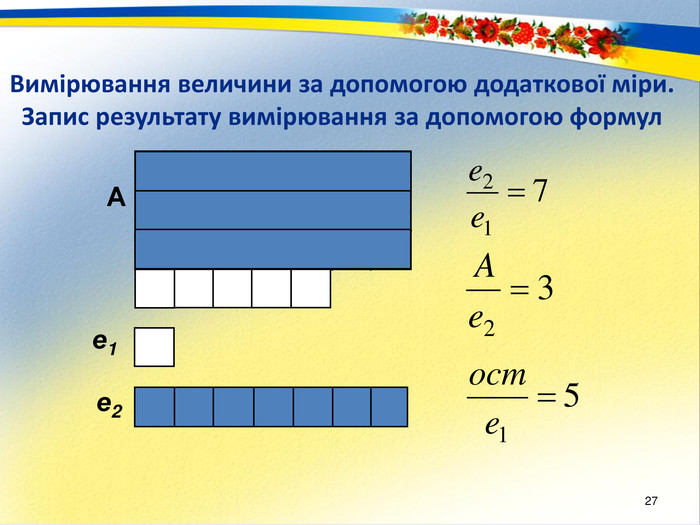
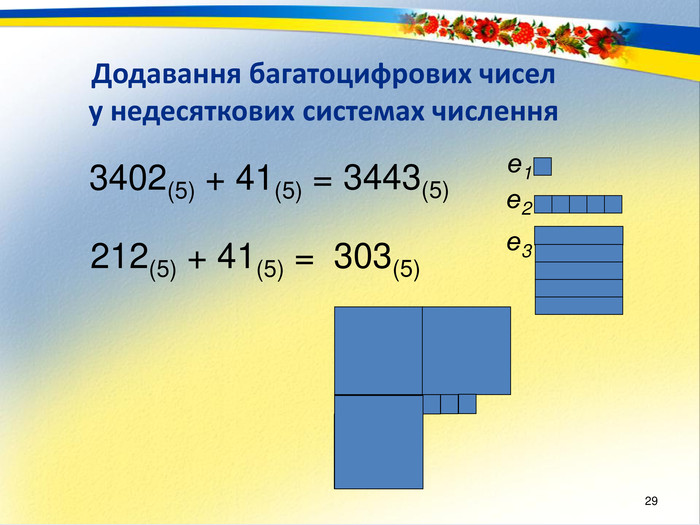
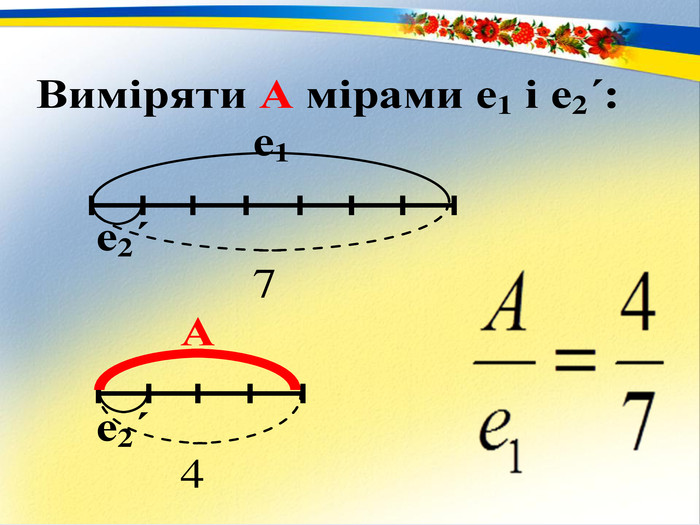
Раціональне число. Основним змістом програми розвивального навчання математики є поняття раціонального числа. Формування цього поняття забезпечується аналізом генетично вихідного для всіх видів чисел відношення – відношення величин. Результат вимірювання величини деякою мірою, тобто відношення величини до міри – це число. Вимірювання величин деякою мірою за різних умов дає отримання різних видів чисел.

ДОЧИСЛОВИЙ ПЕРІОДВеличини;Порівняння величин; Додавання, віднімання величин

Порівняння величин. А ≠ KА > K A =K =AKTK + TA - TTA – М = K + МММДодавання величин. Віднімання величин

Властивості віднімання. Віднімання суми. АВСМА – М – C = А – (М + C) А – М – C = BKK = М + CА – (М + C) = B

22 Типи задач на додавання і віднімання. BCABCAА = В + СC = A - BЗадача на знаходження цілого. Задача на знаходження частини

Число. Результат вимірювання величини деякою мірою. Відношення величини до міри

Число як відношення величини до міриe. Ae=8 An. An=4k. Ak=2

Число як відношення величини до міри забезпечує розуміння наявності різних систем числення012 1④ 1 3⑥21④13⑥=

Дії з числами як моделювання дій з величинами2612(5) + 31(5) =43(5)222(5) + 41(5) =313(5)е1е2е32 5 3

27 Вимірювання величини за допомогою додаткової міри. Запис результату вимірювання за допомогою формул. Ае1е2

28 Ае1е2 По 7 взяти 3 рази і ще 5 Вимірювання величини за допомогою додаткової міри. Запис результату вимірювання за допомогою числового виразу

Додавання багатоцифрових чисел у недесяткових системах числення293402(5) + 41(5) =3443(5)212(5) + 41(5) =303(5)е1е2е3

ЗВИЧАЙНІ ДРОБИВведення додаткової міри для вимірювання меншої величини;Запис результату вимірювання звичайним дробом;Порівняння, додавання, віднімання звичайних дробів.

31 Система додаткових зменшених мір. Позиційний дрібе1е2е3е4е1 е´2 е´3 е´4. , . . .

4 – кількість зменшених мірок7 – на скільки поділено одиничну мірку

Додавання і віднімання звичайних дробів з однаковими знаменниками01

Група 1 Група 4 Основна властивість дробу

Відсотки 100 %

Раціональні числа

Використання робочих зошитів    

Метод роботи на уроці у системі РН «пошуковий», «дослідницький». Відкриття не виникають поодинці. Тому на уроках використовуються різні форми роботи – парна, групова, робота в команді.

Згідно психологічних досліжень: Якщо самооцінка дитини оптимальна, тоді вона сприяє її саморозвитку і самореалізації. Низька ж самооцінка є суттєвою перешкодою для самореалізації.

Переваги системи Д. Б. Ельконіна – В. В. Давидова. Діти навчаються не розгублюватись, потрапляючи в нову для себе ситуацію, вони здатні самостійно проаналізувати обставини, що склалися, і знайти вирішення для подолання труднощів.

Діти стають впевненішими у своїх знаннях і здібностях. У тому числі через те, що висловлена на уроці, навіть невірна, гіпотеза стає не предметом різкої критики, а кроком до глибшого розуміння предмету, що вивчається.

Тож нехай кожна сходинка, якою підніматимуться наші учні, буде сходинкою успіху і даруватиме їм радість від навчання!r

ЛІТЕРАТУРА: Давыдов В. В. Теория развивающего обучения. / В. В. Давыдов. – М.: ИНТОР, 1996. – 544 с. Александрова Е.І. Методика навчання математиці в початковій школі. (Система Д. Б. Ельконіна – В. В. Давидова): Посібник для вчителя. – М.: Вита – Пресс, 2002. Ельконін Б. Д. Поняття компетентності з позицій розвивального навчання. / Д. Б. Ельконін // Практика розвивального навчання. Збірник статей // За ред. О. К. Дусавицького. – Харків, 2004. Семенець С. П. Теорія задач розвивальної математичної освіти / С. П. Семенець // Дидактика математики: проблеми і дослідження: Міжнар. зб. наук. робіт. - Вип. 30. - Донецьк: Вид-во Дон. НУ, 2008. - С. 130-134. Дусавицький О. К. Особливості застосування системи розвивального навчання в шкільній практиці // Практика розвивального навчання. Збірник статей. – Харків: ХНУ ім. В. Н. Каразіна, 2004. – С. 16 – 19. Г. В. Жемчужкіна, К. І. Мельник «Робочий зошит з математики для 6 класу Система розвивального навчання Д. Б. Ельконіна – В. В. Давидова. – Харьків: ННМЦ «Розвиваюче навчання », 2012. Кондратюк Е. М., Толмачева З. И «Урок в системе развивающего образования» / под ред А. К. Дусавицкого, - Харьков, 2002 /