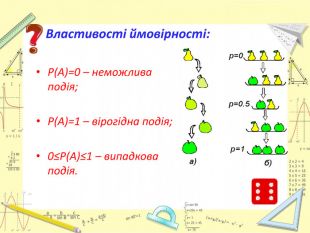
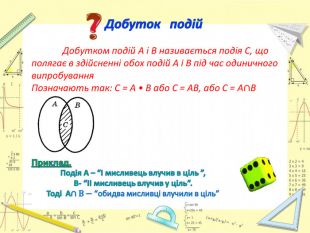
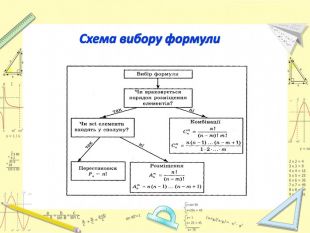
Презентація "Обчислення ймовірності за допомогою комбінаторики. Ймовірність суми та дообутку подій"
Про матеріал
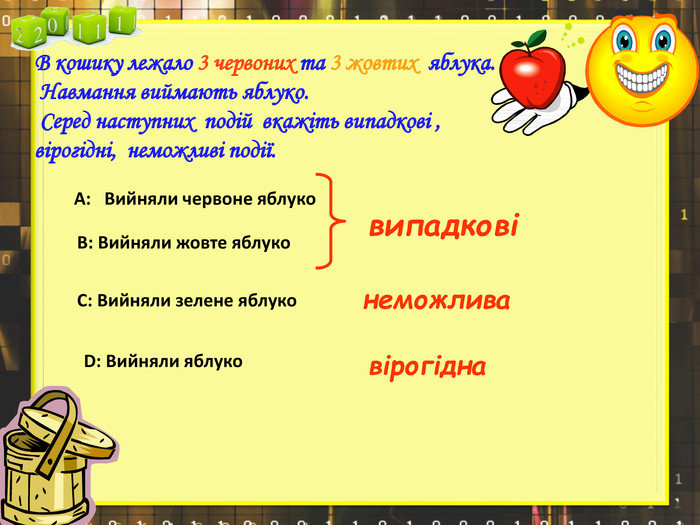
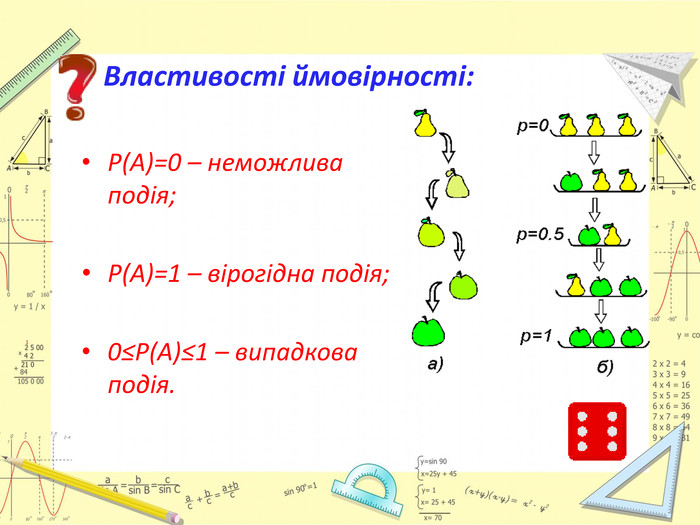
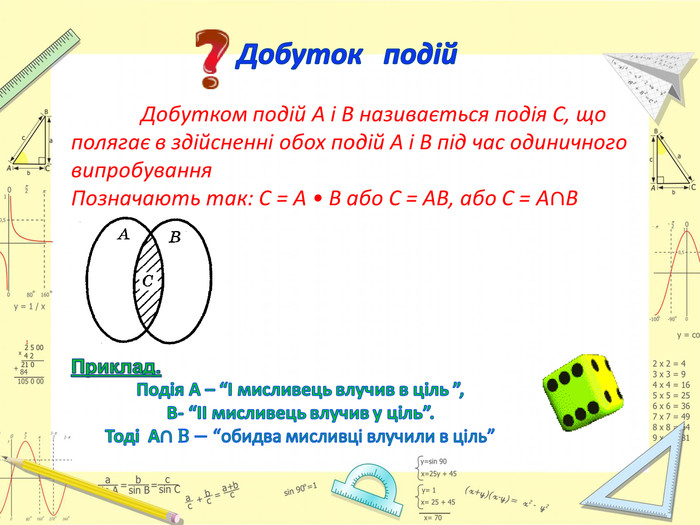
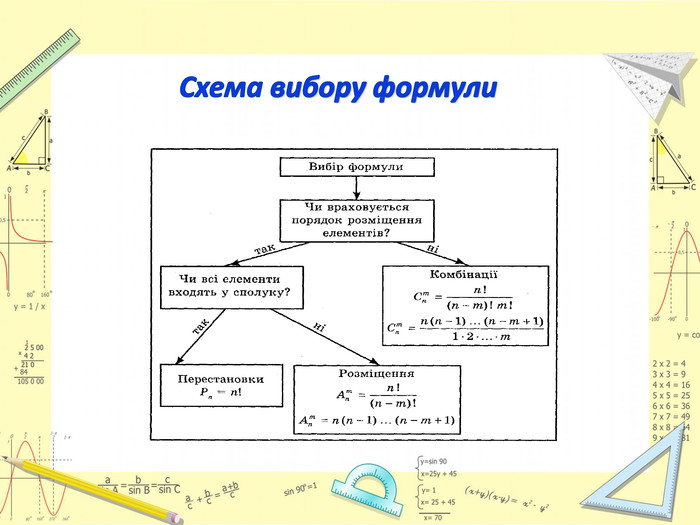
Презентація до заняття відображає всі етапи його проведення, містить яскраві та доречні ілюстрації, запитання та відповіді до опитувань, умови та розв'язки практичних завдань.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку