УРОК "РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ЗАСТОСУВАННЯ ФІЗИЧНОГО ТА ГЕОМЕТРИЧНОГО ЗМІСТУ ПОХІДНОЇ, ОБЧИСЛЕННЯ ПОХІДНИХ СКЛАДЕНИХ ФУНКЦІЙ"
Методична розробка передбачає проведення практичного заняття з
використанням інтерактивних методів навчання, які сприяють розвитку творчих
здібностей студентів, стимулюють пізнавальну активність і самостійність.
Рекомендовано для викладачів навчальних закладів I-II рівнів акредитації.
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
МОГИЛІВ – ПОДІЛЬСЬКИЙ ТЕХНОЛОГО – ЕКОНОМІЧНИЙ КОЛЕДЖ
ВІННИЦЬКОГО НАЦІОНАЛЬНОГО АГРАРНОГО УНІВЕРСИТЕТУ
РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ЗАСТОСУВАННЯ ФІЗИЧНОГО ТА ГЕОМЕТРИЧНОГО ЗМІСТУ ПОХІДНОЇ, ОБЧИСЛЕННЯ ПОХІДНИХ СКЛАДЕНИХ ФУНКЦІЙ
МЕТОДИЧНА РОЗРОБКА ВІДКРИТОГО ЗАНЯТТЯ
З ДИСЦИПЛІНИ ”МАТЕМАТИКА”
2018
Автор: Кордонська Ірина Василівна, викладач математики,
спеціаліст вищої категорії, викладач-методист
Рецензент: Романенко Лілія Леонідівна, викладач фізики, спеціаліст
першої категорії
Методична розробка передбачає
проведення практичного заняття з
використанням інтерактивних методів
навчання, які сприяють розвитку творчих
здібностей студентів, стимулюють
пізнавальну активність і самостійність.
Рекомендовано для викладачів навчальних
закладів I-II рівнів акредитації.
Розглянуто і схвалено на засіданні
циклової комісії природничо – наукових
та загальноекономічних дисциплін
Протокол № ___ від _________2018
Голова ц/к ____________/Носкова Т.А./
Дисципліна. Математика.
Дата: 12.04.2018р.
Група: ТЗ 65/9-17
Методична мета заняття: реалізація елементів інформаційно – комунікативних технологій на практичних заняттях; застосування активних форм і методів виховання особистості компетентного спеціаліста.
Тема заняття: РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ЗАСТОСУВАННЯ ФІЗИЧНОГО ТА ГЕОМЕТРИЧНОГО ЗМІСТУ ПОХІДНОЇ, ОБЧИСЛЕННЯ ПОХІДНИХ СКЛАДЕНИХ ФУНКЦІЙ
Вид заняття: Практична робота
Мета заняття:
Навчальна - перевірити знання студентами формул для знаходження похідної та вміння застосовувати методи диференціального числення до розв’язування прикладних задач, вміння складати алгоритм розв’язування прикладних задач;
Розвиваюча - формувати вміння міркувати, аналізувати й робити висновки; розвивати творчі здібності й логічне мислення, кругозір студентів, усне та писемне мовлення;
Виховна - виховувати активність, увагу, інтерес та бажання мати глибокі й міцні знання, працьовитість та уважність; розвивати інтерес до математики.
Компетенції: навчальна, інформаційна, стимулювально – мотиваційна.
Функції:
Теоретична - Знати: формули диференціювання простих та складених функцій, алгоритми розв’язування практичних задач за допомогою похідної.
Практична: вміти: застосовувати формули диференціювання для обчислення похідних складених функцій застосовувати алгоритми розв’язування практичних задач на застосування похідної
Міжпредметні зв’язки.
Забезпечуючі: Алгебра 10 клас . Т.1. Функція
Геометрія 8 клас . Пряма.
Забезпечувані: Фізика: Т. Змінний струм.
Вища математика: Тема 5. Диференціальне числення
Забезпечення заняття.
- 1. Література: М.І.Шкіль. Алгебра і початки аналізу 11 кл.
О.М. Роганін. Плани – конспекти уроків.
Т.Г.Роєва. Алгебра в таблицях.
М.В.Богомолов. Практичні заняття з математики.
Г.Н.Яковлев. Алгебра і початки аналізу.1 частина
2. Наочні посібники: презентація: “Розв’язування задач на застосування фізичного та геометричного змісту похідної, обчислення похідних складених функцій”
3. Роздатковий матеріал: інструкції, варіанти завдань для письмового
опитування; опорні конспекти “ Основні формули
диференціювання ”, картки гри “Доміно”.
4. Технічні засоби навчання: мультимедійний проектор.
Хід заняття
I. Організаційна частина заняття. - 2 хв.
(Метод: психолого – педагогічної підтримки роботи студентів на занятті.)
1.1 Перевірка наявності студентів, відповіді на запитання студентів.
1.2 Мобілізація студентів до праці, активізація уваги, створення робочої атмосфери.
Кожен із студентів на протязі заняття отримає оцінку, яка буде складатися із отриманих балів за правильні відповіді під час колективної роботи та виконання індивідуальних завдань.
У вас на столах лежать різні смайлики , які означають: веселий – «Я все знаю і все розумію», допитливий – «Мені дещо незрозуміло», сумний – «Мені важко зрозуміти цю тему». Визначте рівень своїх знань на початок уроку.
ІI. Перевірка домашнього завдання (метод –вибіркова перевірка домашніх вправ, обговорення проблемних питань до домашньої роботи )
ІIІ. Підготовка студентів до заняття. - 25 хв.
2.1 Повідомлення теми, мети заняття та комплексу завдань.
Метод – інструктування.
Тема заняття: Розв’язування задач на застосування фізичного та геометричного змісту похідної, обчислення похідних складених функцій
Мета заняття: Узагальнити та систематизувати знання студентів про фізичний та геометричний зміст похідної, обчислення похідних складених функцій
2. 2 Вступний інструктаж
2.2.1 Мотивація навчальної діяльності студентів.
Методи: бесіда, проблемний, переконання, історично - довідниковий
Математичний аналіз - це розділ математики, у якому вивчається диференціальне й інтегральне обчислення. Створили це числення у XVII столітті, практично водночас і незалежно один від одного Ісаак Ньютон у Англії й Гофрід Лейбніц у Німеччині. Це стало можливим завдяки раніше введеному поняттю функції. Термін «похідна» ввів Луї Лагранж у 1791 році.)
У XV—XVII століттях в Європі зміцнювався новий суспільний лад — капіталізм. Назрівала технічна революція. Відбувалося вдосконалення виробництва на базі винаходу парових машин, тобто потрібно було вирішувати проблеми практичної спрямованості в гідротехніці, мореплавстві, військовій справі (обчислення траєкторії польоту кулі, швидкості її руху). Головним є те, що слід було досліджувати зміну різних функцій.)
Таким чином стало можливим дослідження поведінки диференційованої функції без наглядного їх вигляду.
Розвиток математичних обчислень є процесом, що має діалектичний характер. У рамках уже відомого матеріалу відбувається накопичення передумов для нового обчислення. Останнім етапом періоду нової теорії є встановлення зв'язку й взаємозворотності диференціальних та інтегральних досліджень. Потім відбувається переворот у методі. Обчислення виходить за межі практичних потреб, а галузь використання обчислень, як правило, стає більш широкою, ніж галузь, яка їх породила. Одне із джерел розвитку науки — це життя. Воно ставить завдання, а наука їх вирішує.
2.2.1. Реалізація міжпредметних зв’язків . Метод - логічної градації


![]()


![]()
![]()
![]()



2.2.3. Прикладне спрямування теми у формуванні майбутнього компетентного фахівця.
Методи: переконання, постановка проблеми.
Оскільки ми вже говорили про те, що основна задача похідної та диференціального числення – це вивчення швидкості зміни будь якої диференційованої функції, то також за допомогою похідної можна досліджувати різноманітні технологічні та економічні процеси на виробництві.
2.2.4. Актуалізація опорних знань та вмінь студентів
Метод: теоретичний пазл, доміно.
- Повторення формул диференціювання
|
№ п/п |
функція |
Похідна функції |
|
1 |
с |
? |
|
2 |
? |
1 |
|
3 |
|
? |
|
4 |
|
? |
|
5 |
? |
|
|
6 |
|
? |
|
7 |
? |
|
|
8 |
? |
|
|
9 |
|
? |
|
10 |
sinx |
? |
|
11 |
? |
-sinx |
|
12 |
tgx |
? |
Очікувані результати
|
№ п/п |
функція |
Похідна функції |
|
1 |
с |
0 |
|
2 |
|
1 |
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
sinx |
|
|
11 |
|
-sinx |
|
12 |
tgx |
|
- Обчислення похідних складених функцій(гра «Доміно»)
Обчислити похідні функцій:
А) ![]() . Очікуваний результат:
. Очікуваний результат: ![]()
Б) ![]() . Очікуваний результат:
. Очікуваний результат: ![]()
В) ![]() . Очікуваний результат:
. Очікуваний результат:![]()
Г) ![]() . Очікуваний результат:
. Очікуваний результат: ![]()
Д) ![]() . Очікуваний результат:
. Очікуваний результат:![]()
Е)![]() . Очікуваний результат:
. Очікуваний результат: ![]()
ІІІ. Відпрацювання вмінь – 20хв.
Поточний інструктаж і контроль за виконанням роботи.
Метод проведення – керований практикум( робота студентів згідно інструкції для практичної роботи, бесіда, колективне розв'язування вправ, інструктаж щодо виконання завдань).
Студенти приступають до виконання практичної роботи, викладач консультує їх в процесі розв’язування завдань.
Актуалізація опорних знань студентів про фізичний зміст похідної (метод- мікрофон)
- В чому суть похідної?
Очікувана відповідь: похідна вказує зміну функції із зміною аргументу
- Фізичний зміст похідної.
Очікувана відповідь: фізичним змістом похідної є швидкість тіла в даний момент часу (миттєва швидкість)
- Що таке друга похідна від функції?
Очікувана відповідь: другою похідною від функції є її похідна від першої похідної
- Механічний зміст другої похідної.
Очікувана відповідь: механічним змістом другої похідної є прискорення
Задача №1. Знайти похідні складених функцій:
а) ![]() б)
б)![]() в)
в) ![]()
Розв’язування.
а) ![]()
![]() ,
, ![]() ,
, ![]()
![]()
б) ![]()
![]() ,
, ![]() ,
, ![]()
![]()
в) ![]()
![]()
Нехай ![]() , тоді
, тоді ![]() ,
, ![]() ,
, ![]()
![]()
Нехай ![]() , тоді
, тоді ![]() ,
, ![]() ,
, ![]()
![]()
Отже, ![]()
![]()
![]()
Задача №2. Знайти швидкість і прискорення точки, що рухається за законом ![]() в момент часу
в момент часу ![]() с.
с.
Розв’язування.
-
За фізичним змістом похідної
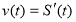 . Тоді
. Тоді 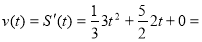
![]() і
і ![]()
-
За механічним змістом другої похідної
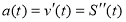
Тоді ![]()
і ![]()
Відповідь: ![]() ,
, ![]()
Актуалізація опорних знань студентів про геометричний зміст похідної
(метод – продовження речення)
- Дотичною до графіка функції є…
Очікувана відповідь: граничне положення січної МК, при якому К прямує до М
- Кутовим коефіцієнтом прямої є …
Очікувана відповідь: тангенс кута нахилу ![]() прямої до додатного напрямку осі ОХ
прямої до додатного напрямку осі ОХ
- Геометричним змістом похідної є …
Очікувана відповідь: кутовий коефіцієнт дотичної до графіка функції в заданій точці
-
Загальний вигляд рівняння дотичної до графіка функції
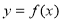 в точці з абсцисою
в точці з абсцисою 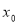 …
…
Очікувана відповідь: ![]()
Задача №3.
а) Скласти рівняння дотичної до графіка функції ![]() в точці з абсцисою
в точці з абсцисою ![]() .
.
б) В яких точках дотична до графіка функції ![]() утворює
утворює
з віссю абсцис кут 450?
Розв’язування
а) загальний вигляд рівняння дотичної :
![]()
1. знаходимо значення функції в заданій
точці: ![]()
![]()
2. знаходимо похідну функції та її
значення в заданій точці:
![]()
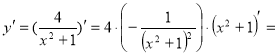
=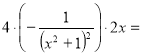
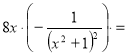
![]()
![]()
![]()
3.Записуємо рівняння дотичної до
графіка функції: ![]() .
.
Звідки матимемо: ![]()
Відповідь: ![]()
б) Якщо дотична до графіка функції
утворює кут 450, то її кутовий
коефіцієнт буде ![]() .
.
Тоді, використовуючи геометричний
зміст похідної, ![]() .
.
Тоді ![]()
звідки ![]() або x=1.якщо x=1,
або x=1.якщо x=1,
![]() .
.
Точка (1;1)- шукана.
Відповідь: (1;1)
3.2. Заключний інструктаж - 1хв
Метод: формування професійних компетенцій (переконання).
Зверніть увагу, що всі задачі на практичне застосування похідної носять алгоритмічний характер. Тобто є чіткий план досягнення мети. Прошу у ваших індивідуальних завданнях дотримуватись відповідних алгоритмів при виконанні вправ.
Підводяться підсумки роботи, записуються відповіді, висновки.
ІV. Самостійна робота. – 20хв
Метод – письмове опитування по варіантах. (6 варіантів)
В-1 В-2
- Знайти похідні функцій:
а) ![]() а)
а)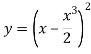
б) ![]() б)
б)![]()
в) ![]() в)
в)![]()
2. Знайти швидкість і прискорення точки, що рухається за законом
![]() в момент часу
в момент часу ![]() .
.
![]()
![]()
3.Скласти рівняння дотичної до кривої в точці з абсцисою ![]() .
.
![]()
![]()
В-3 В-4
- Знайти похідні функцій:
а) ![]() а)
а)![]()
б) ![]() б)
б)![]()
в) ![]() в)
в)![]()
2. Знайти швидкість і прискорення точки, що рухається за законом
![]() в момент часу
в момент часу ![]() .
.
![]()
![]()
3.Скласти рівняння дотичної до кривої в точці з абсцисою ![]() .
.
![]()
![]()
В-5 В-6
- Знайти похідні функцій:
а) ![]() а)
а)![]()
б) ![]() б)
б)![]()
в) ![]() в)
в)![]()
2. Знайти швидкість і прискорення точки, що рухається за законом
![]() в момент часу
в момент часу ![]() .
.
![]()
![]()
3.Скласти рівняння дотичної до кривої в точці з абсцисою ![]() .
.
![]()
![]()
V. Підведення підсумків заняття. – 2хв.
Систематизація знань студентів з даної теми. Метод – змістовний пазл




![]()
![]()
![]()




![]()

![]()
![]()
![]()
![]()

![]()
Відбувається рефлексія.
Викладач підводить підсумки заняття, відмічає роботу студентів, коментує отримані оцінки на занятті.
VІ. Домашнє завдання. – 1хв.
Рівень А.
№1. Обчислити похідні функцій: а) ![]() , б)
, б) ![]()
№2. Скласти рівняння дотичної до графіка функції ![]() в точці з абсцисою
в точці з абсцисою ![]()
Рівень Б. Підготувати реферати на тему «Цікаві історичні факти з біографії вчених» (Ньютона, Лейбніца, Лагранжа — на вибір).
Додаток 1
ПРАКТИЧНА РОБОТА №16
Тема. Розв’язування задач на застосування фізичного та геометричного змісту похідної, обчислення похідних складених функцій
Мета роботи: навчитись розв’язувати задачі на геометричні та фізичні застосування похідної.
Наочне забезпечення та обладнання:
- Інструкційні картки;
- Приклади задач;
- Роздаткові матеріали: опорні конспекти «Основні формули диференціювання»
- Обчислювальні засоби: калькулятор.
Теоретичні відомості про похідну. Методичні вказівки до виконання роботи
Нехай U та V – диференційовані функції, С-стала, тоді:
1. ![]()
2. ![]()
3. ![]()
4. 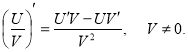
Основні формули диференціювання.
1. ![]() 9.
9. ![]()
2. ![]() 10.
10. ![]()
3. ![]() 11.
11. ![]()
4. ![]() 12.
12. ![]()
5. ![]() 13.
13. ![]()
6. ![]() 14.
14. ![]()
7. ![]()
8. ![]()
Правило диференціювання складеної функції (композиції)
![]()
Задача №1. Знайти похідні складених функцій:
а) ![]() б)
б)![]() в)
в) ![]()
Теоретичні відомості про застосування похідної.
Фізичний зміст похідної. При прямолінійному русі точки швидкість в даний момент ![]() дорівнює похідній
дорівнює похідній ![]() від шляху
від шляху ![]() по часу
по часу ![]() , обчисленій при
, обчисленій при ![]() :
: ![]() .
.
Прискорення ![]() в даний момент
в даний момент ![]() дорівнює похідній
дорівнює похідній ![]() від швидкості
від швидкості ![]() по часу
по часу ![]() , обчисленій при
, обчисленій при ![]() :
: ![]() .
.
Задача №3. Знайти швидкість і прискорення точки, що рухається за законом ![]() в момент часу
в момент часу ![]() .
.
Геометричний зміст похідної. Похідна ![]() дорівнює кутовому коефіцієнту
дорівнює кутовому коефіцієнту ![]() дотичної до кривої, проведеної у точці
дотичної до кривої, проведеної у точці ![]() . Рівняння дотичної до графіка функції
. Рівняння дотичної до графіка функції ![]() в точці з абсцисою
в точці з абсцисою ![]() має вигляд:
має вигляд:![]() .
.
Задача №4.
а)Скласти рівняння дотичної до графіка функції ![]() в точці з абсцисою
в точці з абсцисою ![]() .
.
б) В яких точках дотична до графіка функції ![]() утворює з віссю абсцис кут 450?
утворює з віссю абсцис кут 450?
 Питання для самоконтролю знань і вмінь
Питання для самоконтролю знань і вмінь
- Похідна суми, добутку, частки двох функцій.
- Похідна складеної функції.
- Похідна степеневої функції.
- Похідні логарифмічної, показникової та тригонометричних функцій.
- Фізичний зміст похідної.
- Геометричний зміст похідної. Рівняння дотичної до графіка функції.
Висновок.______________________________________________________________________________________________________________________________________________________________________________________________
Перевірив викладач___________Оцінка _________ Дата______
Додаток 2
Похідна та її застосування
I. Правила диференціювання.
Нехай U та V – диференційовані функції, С-стала, тоді:
1. ![]() 3.
3. ![]()
2. ![]() 4.
4. 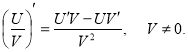
II. Диференціювання складеної функції.
Якщо ![]() - складена функція, то
- складена функція, то ![]()
III. Основні формули диференціювання.
1). ![]() 2).
2). ![]()
3). ![]() 3*).
3*). ![]()
4). ![]() 4*).
4*). ![]()
5). 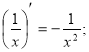 5*).
5*). 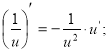
6). ![]() 6*).
6*).![]()
7). ![]() 7*).
7*). ![]()
8). ![]() 8*).
8*). ![]()
9). ![]() 9*).
9*). ![]()
10). ![]() 10*).
10*). ![]()
11). ![]() 11*).
11*). ![]()
12). ![]() 12*).
12*). ![]()
13). ![]() 13*).
13*). ![]()
14). ![]() 14*).
14*). ![]()
15). ![]() 15*).
15*). ![]()
16). ![]() 16*).
16*). ![]()
17). ![]() 17*).
17*). ![]()
IV. Рівняння дотичної до графіка функції ![]() в точці з абсцисою
в точці з абсцисою ![]() .
.
![]()
V. Диференціал функції. ![]() .
.
VI. Застосування диференціала до наближених обчислень.
![]()
Додаток 3
Варіанти самостійної роботи
В-1 В-2
- Знайти похідні функцій:
а) ![]() а)
а)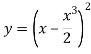
б) ![]() б)
б)![]()
в) ![]() в)
в)![]()
2. Знайти швидкість і прискорення точки, що рухається за законом
![]() в момент часу
в момент часу ![]() .
.
![]()
![]()
3.Скласти рівняння дотичної до кривої в точці з абсцисою ![]() .
.
![]()
![]()
В-3 В-4
- Знайти похідні функцій:
а) ![]() а)
а)![]()
б) ![]() б)
б)![]()
в) ![]() в)
в)![]()
2. Знайти швидкість і прискорення точки, що рухається за законом
![]() в момент часу
в момент часу ![]() .
.
![]()
![]()
3.Скласти рівняння дотичної до кривої в точці з абсцисою ![]() .
.
![]()
![]()
В-5 В-6
- Знайти похідні функцій:
а) ![]() а)
а)![]()
б) ![]() б)
б)![]()
в) ![]() в)
в)![]()
2. Знайти швидкість і прискорення точки, що рухається за законом
![]() в момент часу
в момент часу ![]() .
.
![]()
![]()
3.Скласти рівняння дотичної до кривої в точці з абсцисою ![]() .
.
![]()
![]()
Рецензія
Методична розробка заняття відповідає всім методичним вимогам проведення занять виду практична робота і складена у повній відповідності до програми з дисципліни ” Математика ”. В розробці відображено всі етапи заняття. Досить вдало проведена мотивація пізнавальної діяльності студентів, де використано: історико – довідниковий матеріал, встановлено реальні міжпредметні зв’язки теми з іншими дисциплінами, які вивчаються в коледжі за допомогою методу логічної градації та застосовано прикладне спрямування теми у формуванні майбутнього компетентного фахівця.
Актуалізація опорних знань студентів проводиться за допомогою активних методів, що пожвавлює роботу студентів на занятті і відповідає вимогам сучасності.
Викладка матеріалу проводиться послідовно на належному науковому рівні із застосуванням інформаційно – комунікативних технологій. В кінці кожного етапу підводиться підсумок. Матеріал теми перекликається з темами геометрії за неповну школу та базується на матеріалі вивченому на попередніх заняттях , тому студенти мають можливість взяти участь у з’ясуванні деяких властивостей та теоретичних фактів.
В методичній розробці висвітлено багато різноманітних форм та методів роботи: інструктування, бесіда, ілюстрація, переконання, історично – довідниковий, інформаційно – комунікативний, самостійна робота, тренувальні вправи, мікрофон, незакінчене речення тощо.
Методична розробка забезпечена всіма необхідними матеріалами візуального супроводження, роздатковими матеріалами. Підготовлено презентацію заняття для мультимедійного проектора.
Дана методична розробка може бути використана для проведення заняття з математики по темі ”Розв’язування задач на застосування фізичного та геометричного змісту похідної, обчислення похідних складених функцій.”
Рецензент /Романенко ЛЛ./


про публікацію авторської розробки
Додати розробку
