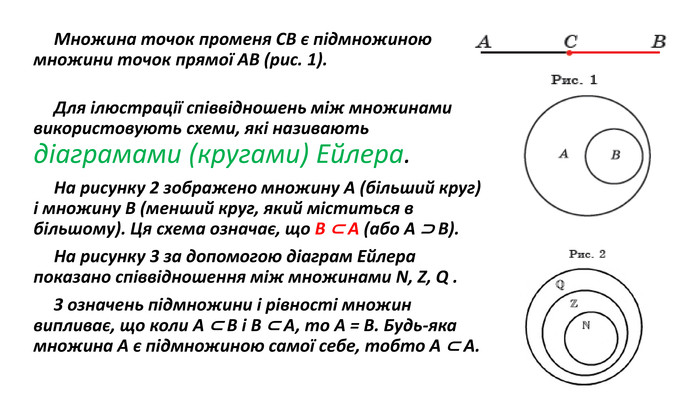
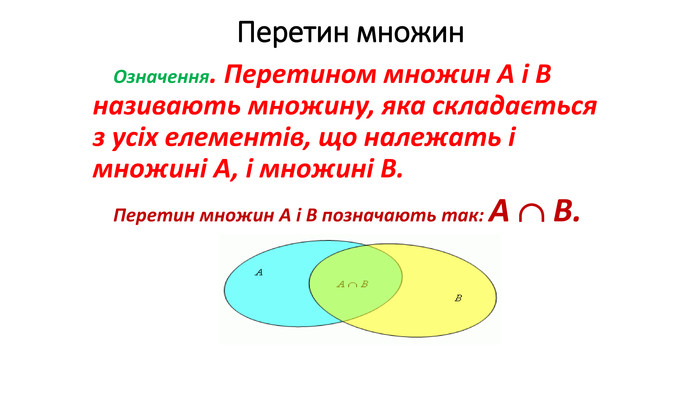
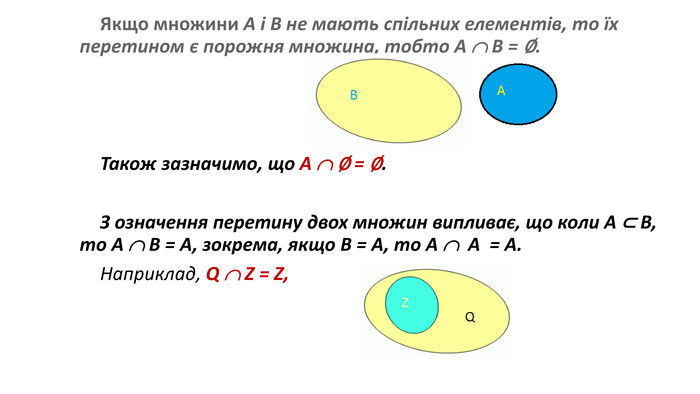
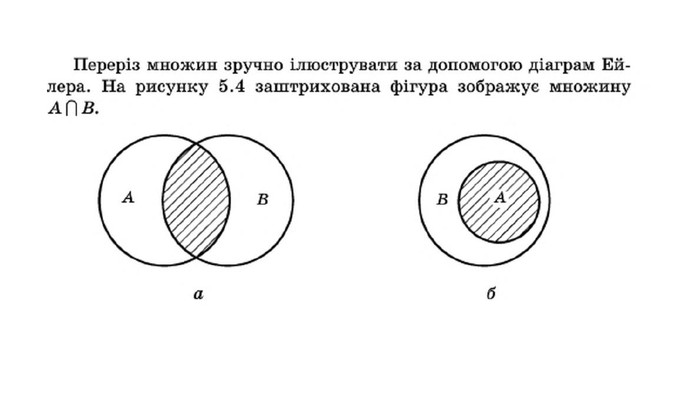
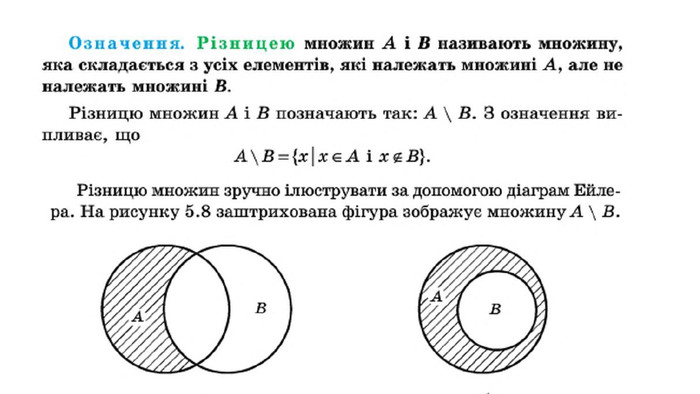
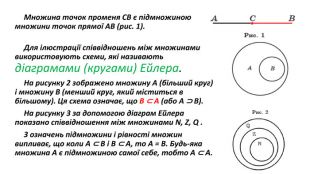
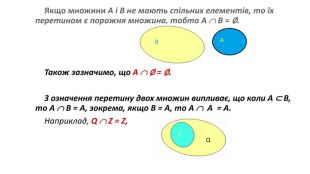
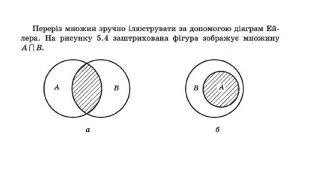
Презентація "Операції над множинами"
Про матеріал
Розробка уроку алгебри на тему: "Об'єднання і переріз множин. Підмножина. Круги Ейлера". Може бути використана в 8 класі з поглибленим вивченням математики Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра (підручник для класів із поглибленим вивченням математики) 8 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
§ 2. Множини та операції над ними Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку