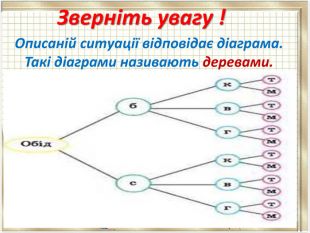
Презентація "Основні правила комбінаторики".

алгебра 9 класвчитель математики Нечитайло В.І. Основні правила комбінаторики.

Мета: сформувати уявлення учнів про комбінаторику, комбінаторні правила суми та добутку; показати широке коло застосування формул комбінаторики у навколишньому світі; розвивати уявлення про математичне моделювання як потужний інструмент розв’язування прикладних задач; виховувати упевненість у власних силах.

КОМБІНАТОРИКА –це розділ математики, присвячений розв'язуванню задач вибору та розташування елементів деякої скінченної множини відповідно до заданих правил. Запам'ятайте!

Розглянемо два основних правила, за допомогою яких розв'язуються багато задач із комбінаторики.правило суми та правило добутку

Приклад 1: У місті N є два університети- політехнічний і економічний, абітурієнту подобається три факультети в політехнічному і два – в економічному. Скільки можливостей має абітурієнт для вступу в університет?Розв'язання: Позначимо буквою А множину факультетів, які обрав абітурієнт в політехнічному університеті, а буквою В - в економічному. Тоді А = { m,n,k}, B = { p,s} . Оскільки ці множини не мають спільних елементів, то загалом абітурієнт має 3+2=5 можливостей вступати до університету. Виконаємо разом!

Описану ситуацію можна узагальнити у вигляді твердження, яке називається правилом суми. Якщо елемент деякої множини А можна вибрати m способами, а елемент множини В - n способами, то елемент із множини А або ж із множини В можна вибрати m + n способами. Запам'ятайте!

Правило суми поширюється і на більшу кількість множин. Приклад 2. Плануючи літній відпочинок, родина визначилася з місцями його проведення: в Одесі – 1, в Скадовську – 3, в Яремчі -2, у Затоці -2. Скільки можливостей відпочинку має родина?Розв'язання: Оскільки всі бази відпочинку різні, то для розв'язання задачі досить знайти суму елементів усіх множин, про які йдеться: 1+3+2+2=8. Отже родина може вибирати відпочинок з 8 можливих. Виконаємо разом!

Приклад 3. Від пункту А до пункту В ведуть 3 стежки, а від В до С - дві. Скількома маршрутами можна пройти від пункту А до пункту С?Розв'язання: Щоб пройти від пункту А до пункту В треба вибрати одну з трьох стежок: 1, 2 або 3. Після чого слід вибрати одну з двох інших стежок: 4 чи 5. Усього від пункту А до пункту В ведуть 6 маршрутів, бо 3·2=6. Усі ці маршрути можна позначити за допомогою пар: (1,4);(1,5); (2,4);(2,5); (3,4);(3,5). Виконаємо разом!14 3 25

Узагальнимо описану ситуацію. Якщо перший компонент пари можна вибрати m способами, а другий - n способами, то таку пару можна вибрати m·n способами. Це правило добутку, його часто називають основним правилом комбінаторики. Запам'ятайте!

Правило добутку поширюється і на впорядковані трійки, четвірки та будь-які інші впорядковані множини. Зокрема, якщо перший компонент упорядкованої трійки можна вибрати m способами, другий –n способами, третій – k спобами, то таку впорядковану трійку можна вибрати m·n·k способами. Виконаємо разом!

Приклад 4. Їдальня на обід приготувала 2 перші страви – борщ (б) і суп (с), 3 другі – котлети (к), вареники (в), голубці (г) і 2- десертні – тістечка (т)і морозиво (м), то всього із 3 страв їдальня може запропонувати 12 різних наборів, оскільки 2·3·2=12. Виконаємо разом !

Описаній ситуації відповідає діаграма. Такі діаграми називають деревами. Зверніть увагу !

Приклад 5. Скільки різних поїздів можна скласти з 6 вагонів, якщо кожний з вагонів можна поставити на будь-якому місці?Розв'язання: Першим можна поставити будь-який із 6 вагонів. Другий вагон можна вибрати з решти 5 вагонів. Тому за правилом множення два перших вагонів можна вибрати 6·5 способами. Третій вагон можна вибрати з 4 вагонів, що залишилися. Тому три перших вагони можна вибрати 6·5·4 способами. Продовжуємо подібні міркування, приходимо до відповіді: усього можна скласти 6·5·4 ·3·2 ·1=720 різних поїздів. Виконаємо разом !

Розв’язання останньої задачі звелося до обчислення добутку всіх натуральних чисел від 1 до 6. У комбінаториці подібні добутки обчислюють часто. Добуток усіх натуральних чисел від 1 до n називають n-факторіалом і позначають п!Наприклад:5! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 = 120, 7! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 = 5040. Домовились вважати, що 1! = 1 і 0! = 1. Зверніть увагу !

791. Є дві цифри: 1 і 9. Скількома способами з цих цифр можна скласти: а) одноцифрове число; б) двоцифрове число, щоб цифри у числі не повторювались; в) двоцифрове число, якщо цифри у числі можуть повторюватися?792. У класі 11 хлопців і 10 дівчат. Скількома способами можна делегувати одного учня в шкільний комітет самоврядування?793. У класі 11 хлопців і 10 дівчат. Скількома способами можна делегувати двох учнів у шкільний комітет самоврядування?794. У класі 11 хлопців і 10 дівчат. Скількома способами можна делегувати одну дівчину і одного хлопця в шкільний комітет самоврядування?Виконайте усно.

795. У магазині є три види печива і десять видів цукерок. Сергій хоче купити сестрі печиво чи цукерки. Скількома способами він може це зробити?796. Для завершення формування експедиції в Антарктиду додатково розглядалися заяви 10 претендентів на посаду лікаря, 5 претендентів на посаду повара і 3 претенденти на посаду техніка. Жоден кандидат не претендував одночасно на дві чи більше посад. Скількома способами можна заповнити одне вільне місце в експедиції?797. Скількома способами можна посадити чотирьох дітей на лавці?Виконайте письмово.

798. На вершину гори ведуть 4 стежки. Скількома маршрутами турист може піднятись на гору і спуститися з неї, обираючи для спуску і підйому різні стежки?799. Оленка має 2 спіднички і 3 вишиті блузки. Скільки різних наборів вбрання можна вибрати для виступу в хорі.800. Їдальня приготувала на сніданок 3 другі страви (А, В, С) і два напої (М, K). Скільки різних наборів із таких страв і напоїв можна вибрати на сніданок? Складіть відповідну діаграму-дерево.801. Скількома способами 5 осіб можуть утворити чергу до каси?Виконайте письмово.

1. Які задачі називають комбінаторними?2. Що таке комбінаторика?3. Сформулюйте правило суми.4. Сформулюйте основне правило комбінаторики.5. Наведіть приклад діаграми-дерева.6. Що таке факторіал? Як його позначають?Перевірте себе.