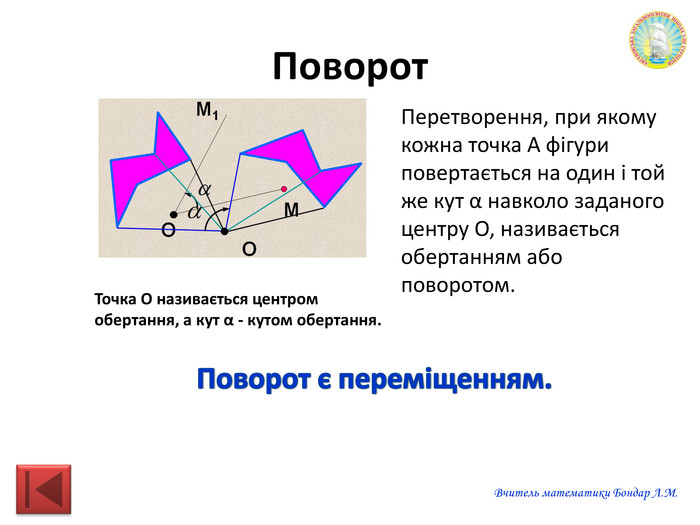
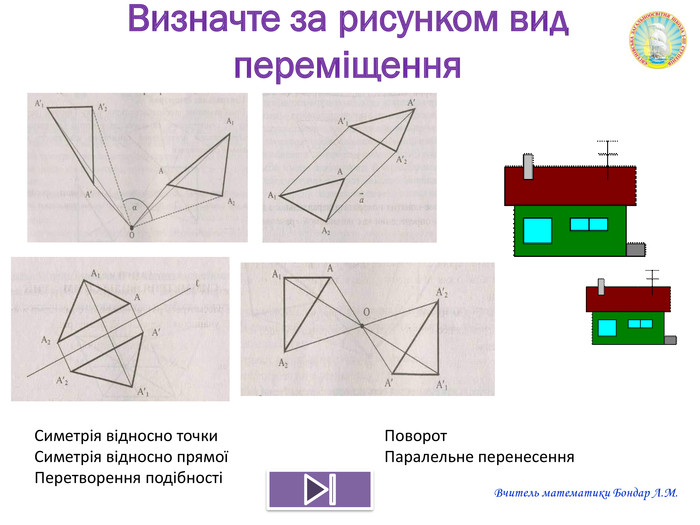
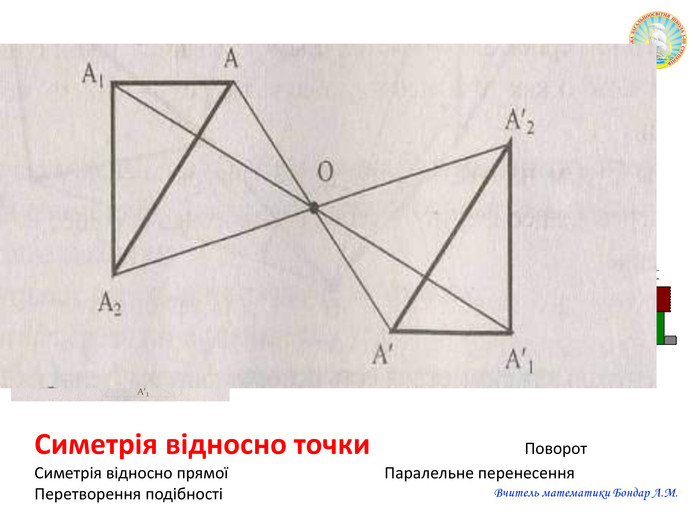
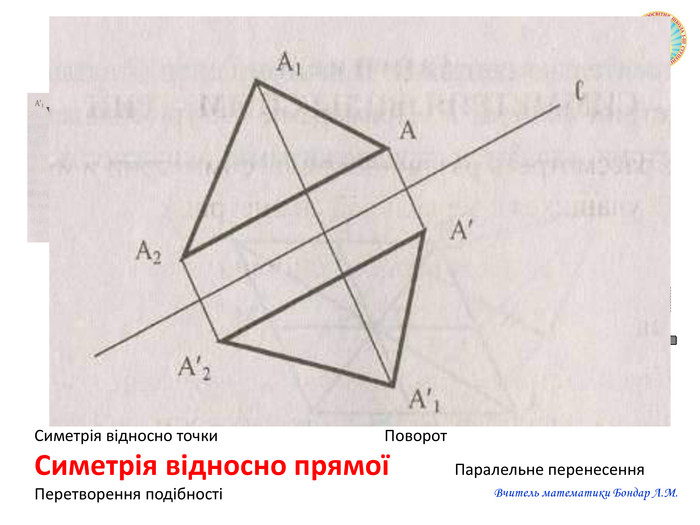
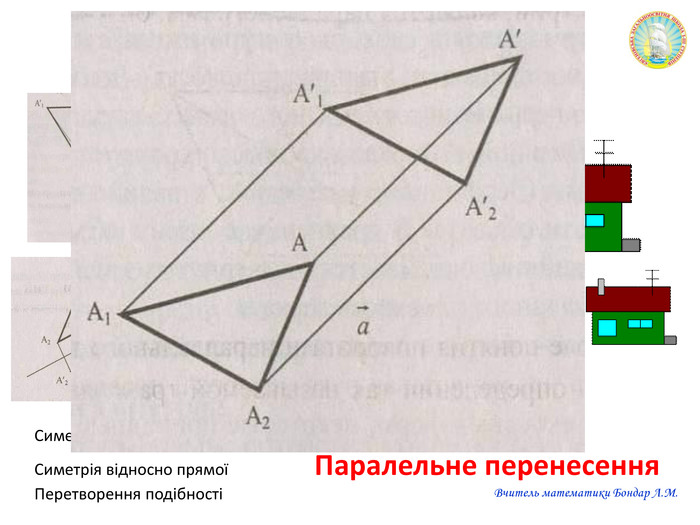
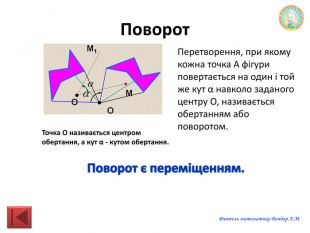
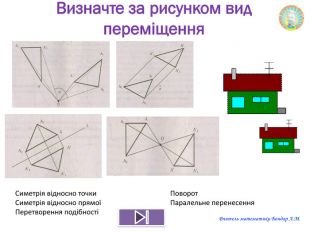
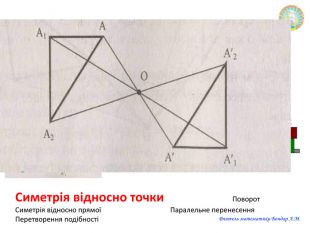
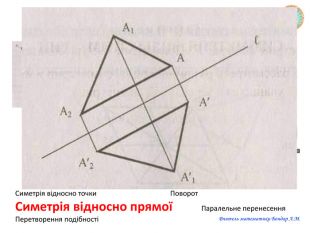
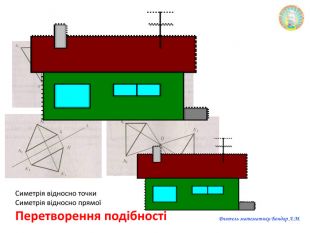
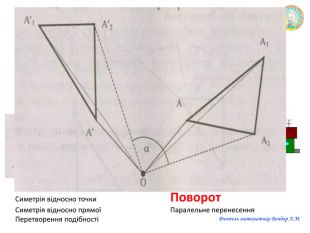
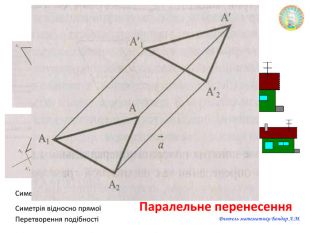
Презентація "Переміщення"
Про матеріал
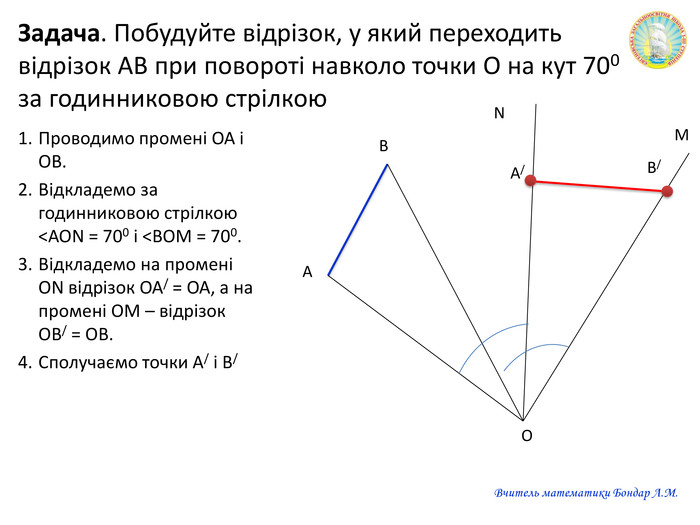
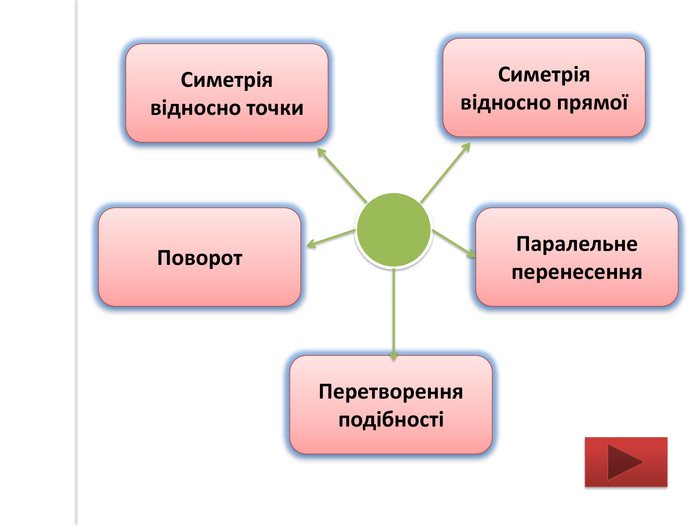
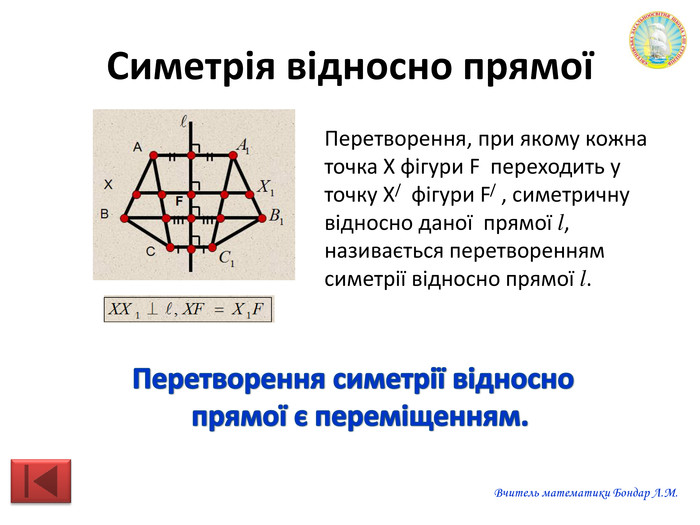
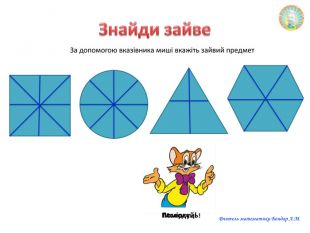
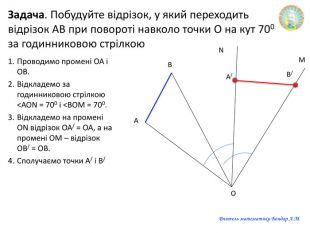
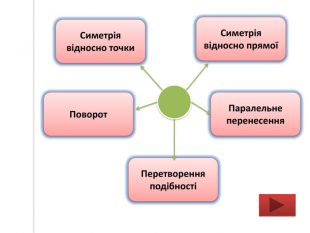
Презентацію можна використати на узагальнюючому уроці з теми "Геометричні перетворення". Завдання для учнів: знайди зайве, визначте за рисунком перетворення спонукають до розвитку критичного мислення. Також в презентації здійнено пошаговий алгоритм побудови поворту. Перегляд файлу
Зміст слайдів
pptx
До підручника
Геометрія 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку