Презентація "Перестановки"
Про матеріал
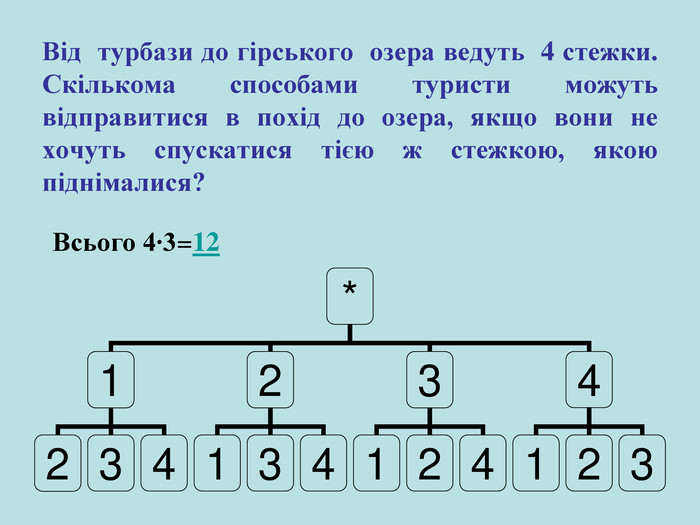
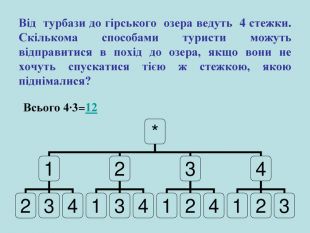
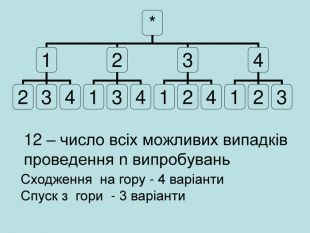
Презентація для уроку алгебри в 9 класі за темою "Комбінаторика". Містить основні відомості про перестановки, приклади розвязування комбінаторних задач на перестановки. Містить завдання на самоконтроль. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку