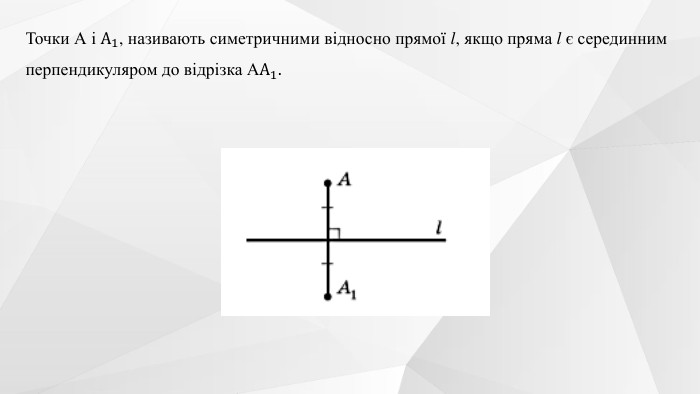
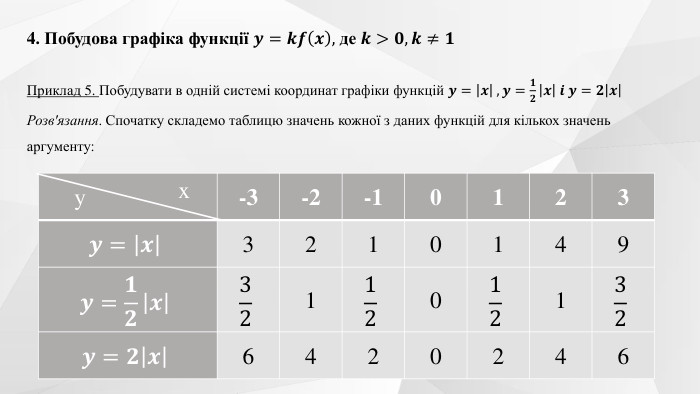
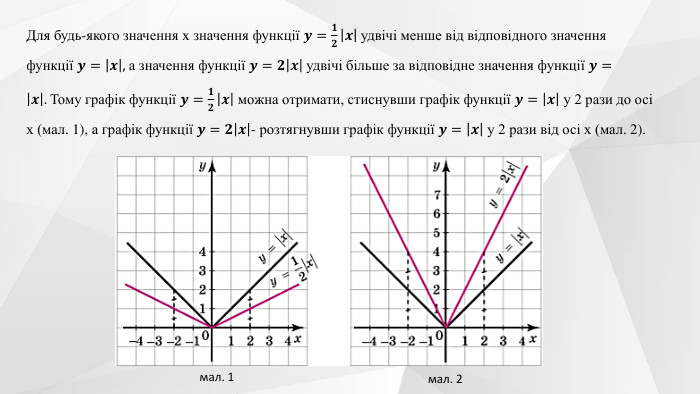
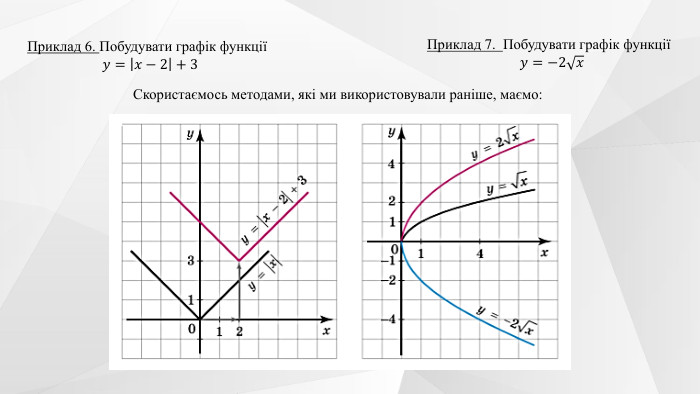
Презентація "Перетворення графіків функцій"
Про матеріал
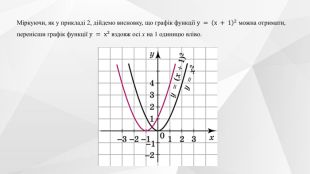
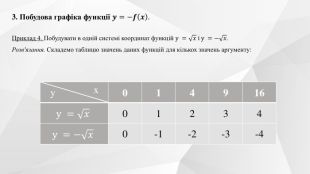
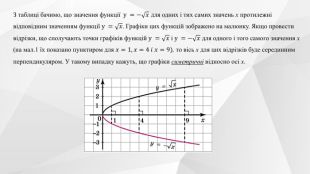
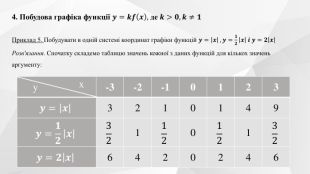
Презентація до уроку на тему "Перетворення графіків функцій".
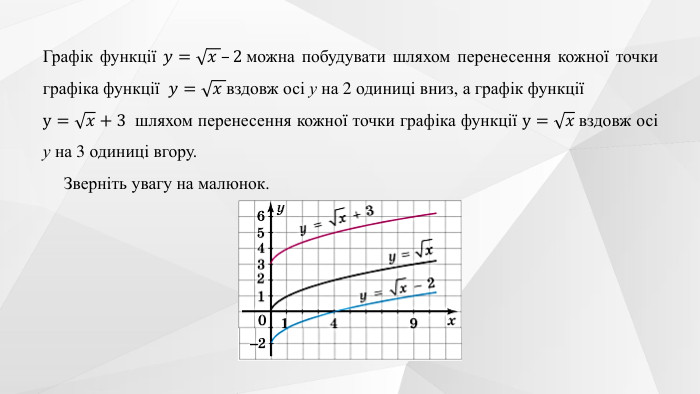
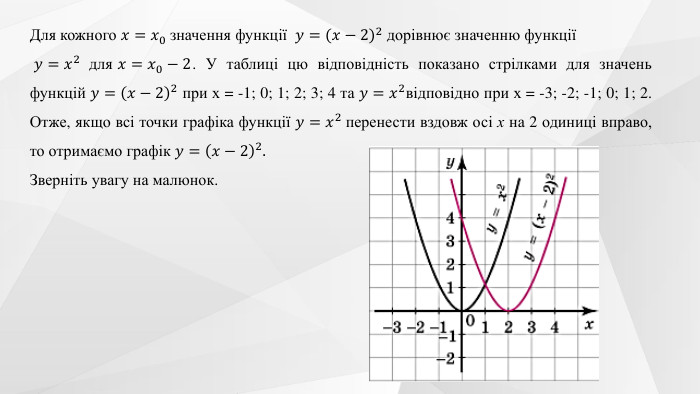
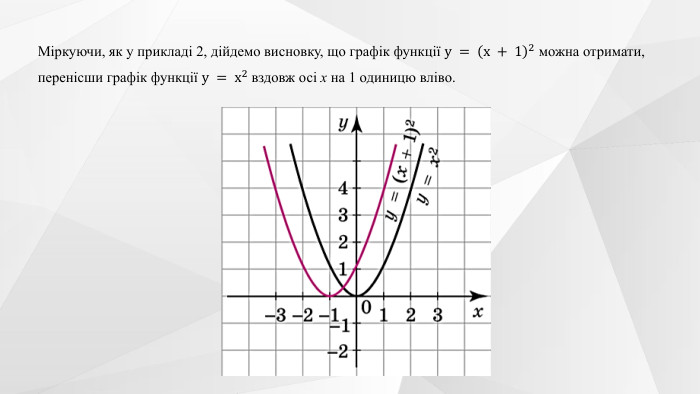
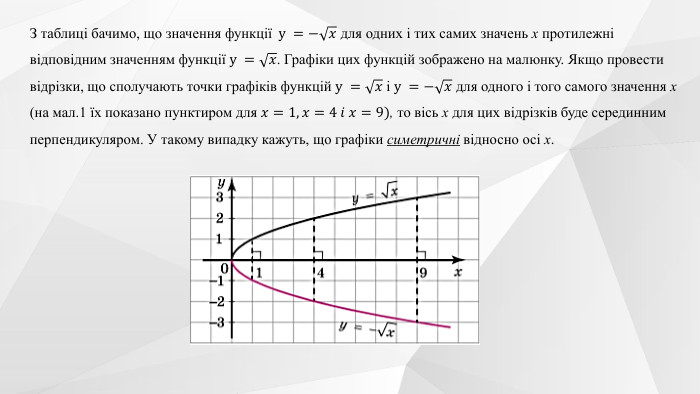
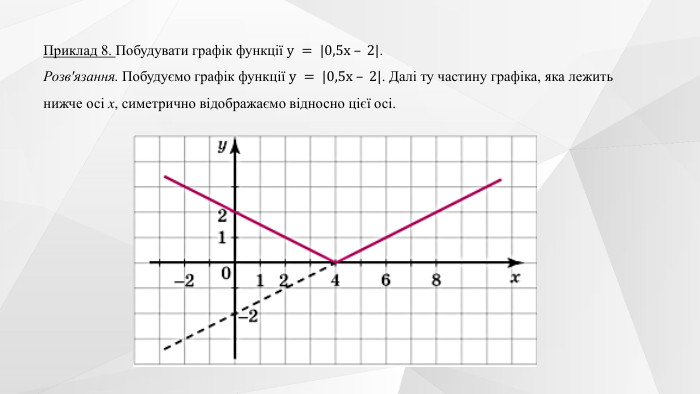
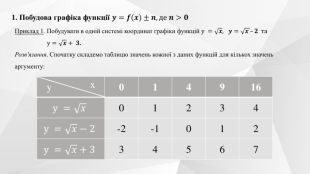
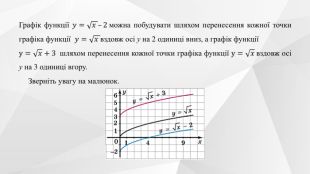
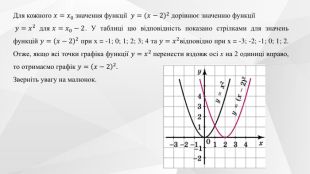
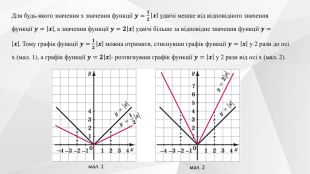
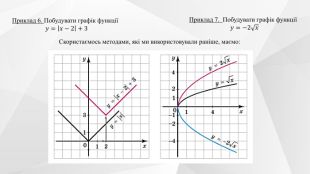
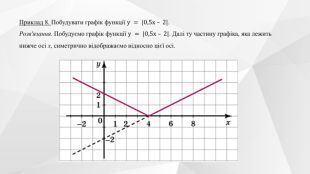
Містить теоретичний матеріал теми, приклади розв'язування типових завдань та побудови графіків функції та вправи для розв'язання. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра 9 клас (Істер О. С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку