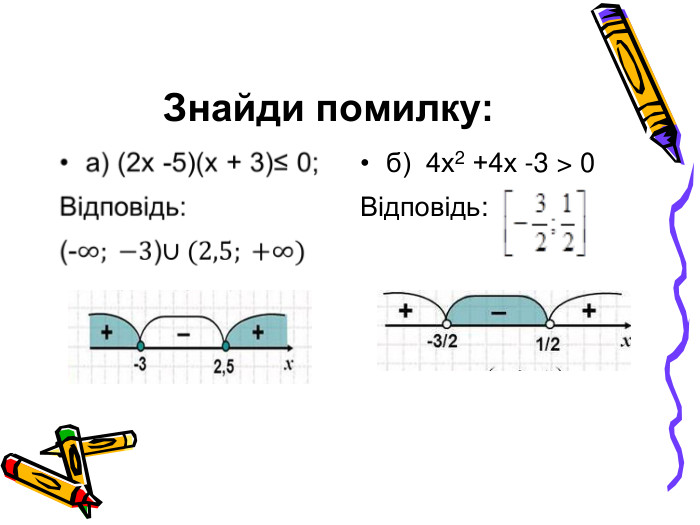
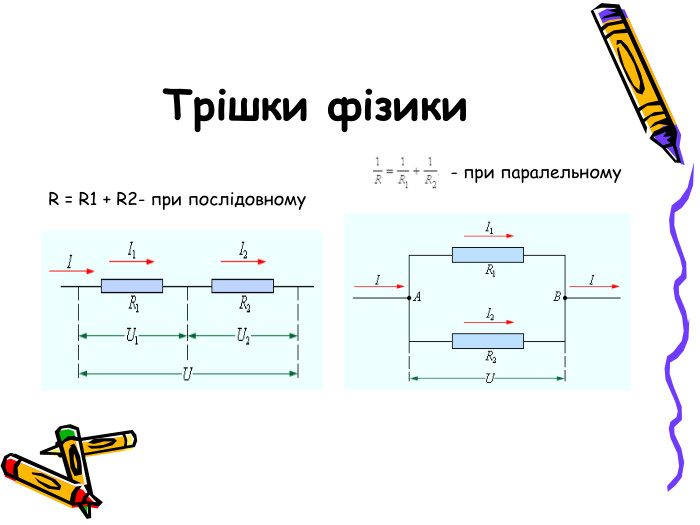
Розв'язування вправ з теми Квадратні нерівності та їх системи.Презентація
Про матеріал
Презентація розроблена для проведення підсумкового уроку по темі "Квадратні нерівності та їх системи". Матеріал містить завдання на узагальнення та систематизації знань, розв'язки до всіх завдань.Презентація може бути корисною для проведення відкритого уроку. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
12. Розв’язування квадратних нерівностей Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку