Презентація "Перетворення тригонометричних виразів"
Про матеріал
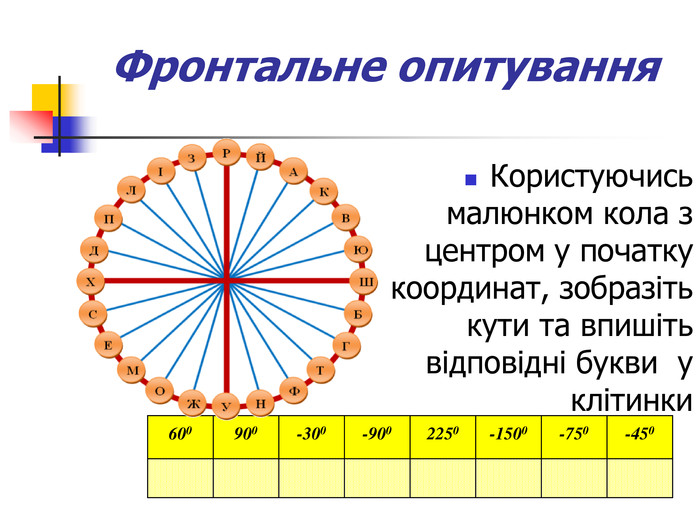
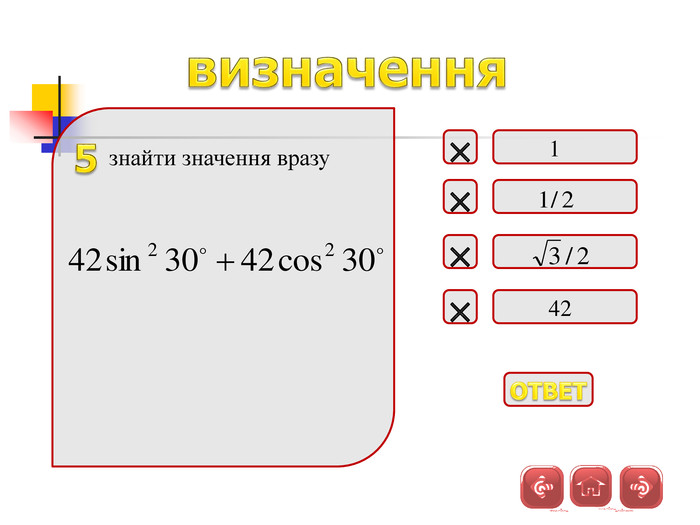
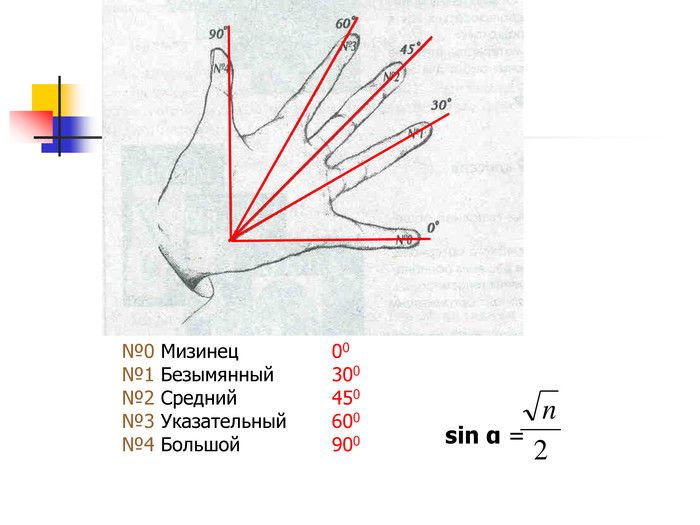
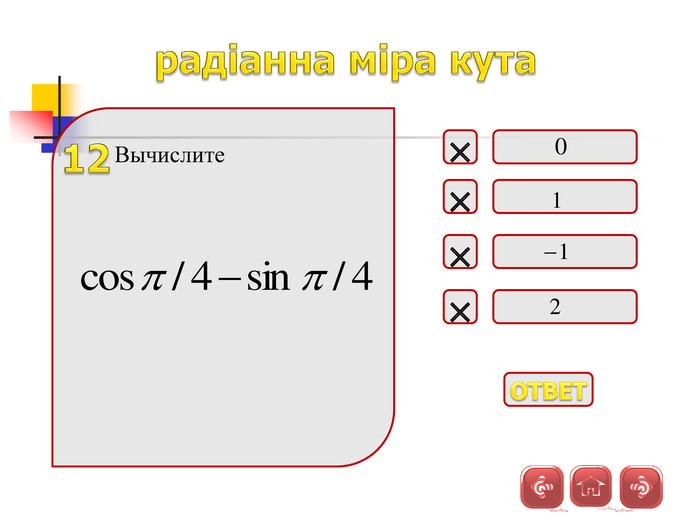
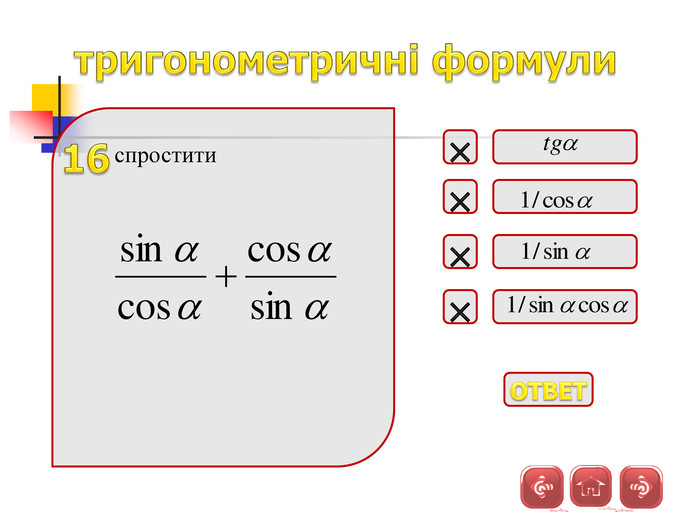
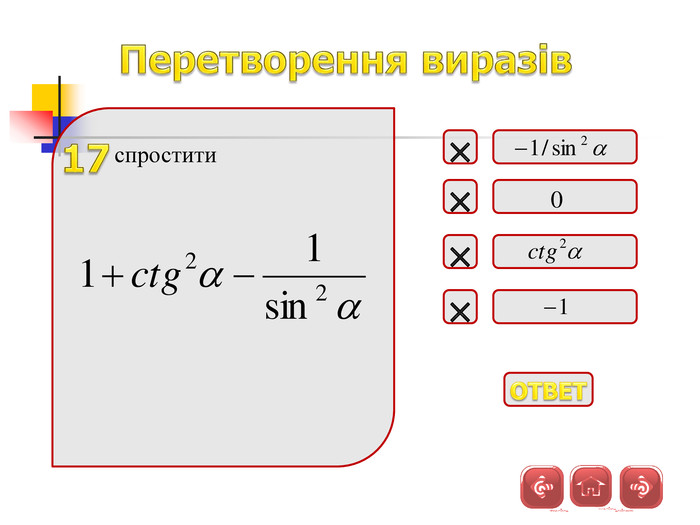
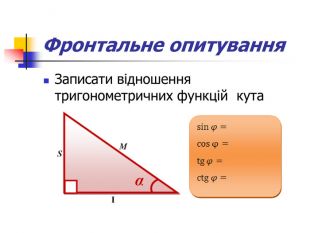
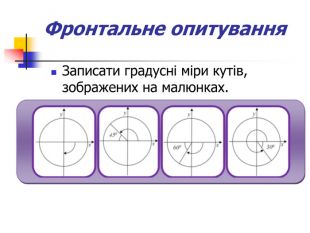
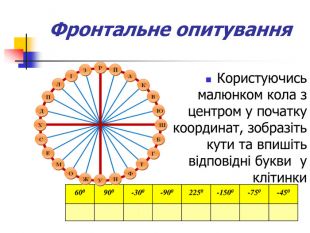
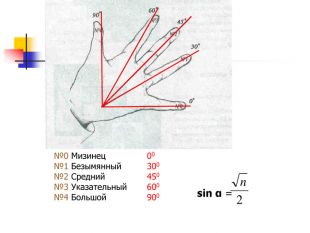
Презентація дозволяє у цікавій формі повторити і закріпити початкові відомості з тригонометрії, Матеріал містить історичну довідку. Стане корисним при підготовці до відкритого уроку, при організації повторення на прикінці навчального року
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дуже дякую за цікавий і корисний матеріал!
ppt
До підручника
Алгебра і початки аналізу (академічний рівень) 10 клас (Нелін Є.П.)
До уроку
§ 20. Співвідношення між тригонометричними функціями одного аргументу Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку