Урок «Теорема о трех перпендикулярах».
Тема урока: «Теорема о трех перпендикулярах».
«Есть истины, как страны,
наиболее удобный путь к
которым становится известным
лишь после того, как мы
испробуем все пути.… На пути к
истине мы почти всегда
обречены совершать ошибки»
Дени Дидро.
Цели урока:
обучающая:
- Знать теорему о трех перпендикулярах и уметь применять ее при решении задач;
- Сформировать видение изученной закономерности в различных ситуациях: при решении задач на доказательство или задач, требующих найти численное (буквенное) значение, какого – либо элемента;
- Учить умению читать чертеж;
- Учить умению объяснять, комментировать выполняемое упражнение в виде цельного связного рассказа.
развивающая:
- Способствовать развитию общения как метода научного познания, аналитико-синтетического мышления, смысловой памяти и произвольного внимания;
- Развивать навыки исследовательской деятельности (выдвижение гипотез, анализ и обобщение полученных результатов).
воспитательная:
- Развивать у учащихся коммуникативные компетенции (культуру общения, умение работать в группах, элементы ораторского искусства);
- Способствовать развитию творческой деятельности учащихся, потребности к самообразованию.
Тип урока: урок изучения и первичного закрепления новых знаний
Технологии:информационные технологии
Оборудование: медиапроектор, экран, мультимедийная программа Microsoft Power Point.
План урока.
- Организационный момент
- Актуализация опорных знаний
- Изучение нового материала
- Закрепление нового материала
- Подведение итогов занятия
- Информация о домашнем задании, инструктаж по его выполнению
ХОД УРОКА
- Организационный момент ( 1 мин.)
Учитель приветствует учащихся и объявляет цель урока и план, используя презентационное сопровождение. Зачитывает эпиграф к уроку.
Учитель. (Слайды 1-3) Сегодня на уроке мы закрепим теорему о трех перпендикулярах, научимся применять теорему о трех перпендикулярах при решении разнообразных задач, вы убедитесь, насколько удобна теорема в использовании и насколько упрощается решение задачи с ее помощью. Эпиграфом к уроку служат слова французского философа-материалиста атеиста Дени Дидро (1713 – 1784) – современника Декарта, Лейбница, личного библиотекаря Екатерины Великой
«Есть истины, как страны, наиболее удобный путь, к которым становится известным лишь после того, как мы испробуем все пути.… На пути к истине мы почти всегда обречены, совершать ошибки» Дени Дидро.
- Актуализация опорных знаний ( 5 мин)
Учитель. Сегодня мы должны вывести и доказать теорему о трех перпендикулярах. А начнем мы с проверки теоретических знаний. (Слайд 4 - 6)
Учитель. Ответьте на вопросы и проведите самооценку своего устного ответа, сопоставив его с выводимыми на экран элементами опорного конспекта.
Учитель объясняет метод теоретического опроса. Подает вопросы по теории на слайдах презентации. Демонстрирует после ответов учащихся соответствующие элементы опорного конспекта.
Учащиеся отвечают на теоретические вопросы устно. После демонстрации правильных ответов ими проводится самооценка своего устного ответа.
Вопросы:
1. Угол между прямыми равен 90°. Как называются такие прямые? (перпендикулярные.)
2. Верно ли утверждение: «Прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости?» (да.)
3. Продолжите предложение: «Прямая перпендикулярна плоскости, если она...» (перпендикулярна к двум пересекающимся прямым, лежащим в этой плоскости).
4. Что можно сказать о двух (3-х, 4-х) прямых, перпендикулярных к одной плоскости? (Они параллельны.)
5. Две прямые, перпендикулярные третьей прямой, … (параллельны)
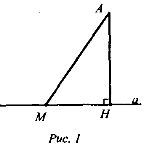
6. Как определяется расстояние от точки до прямой на плоскости? (Возможный ответ: как кратчайшее расстояние от точки до прямой, как длина перпендикуляра, проведенного из точки к данной прямой)
7. Вспомним, как называются отрезки
АМ- ? АН- ? Точка М? Точка – Н ?
Практическая работа. ( 5 мин)
Учитель: Сейчас мы проведём практическую работу, которая позволит нам понять и доказать теорему о тёх перпендикулярах. (Слайд 7).
|
1.Постройте перпендикуляр и наклонную к плоскости листа картона (используя палочки и пластилин). 2.Построите проекцию наклонной на плоскость α. 3.Постройте прямую а в плоскости α, перпендикулярную наклонных и проходящую через её основание. 4.Выскажите предположение о расположении проведённой прямой и проекции наклонной.
По рисунку запишите: наклонная… перпендикуляр… проекция наклонной на плоскость…
Запишите символами: как расположена наклонная к прямойа, По вашему предположению как расположена проекция к прямойа. Выскажите гипотезу. |
IІІ. Изложение нового материала ( 8 мин)
Учитель:Сейчас мы сформулируем и докажем теорему о тёх перпендикулярах.
(Слайд 8-9).
Теорема (о трех перпендикулярах). Прямая,проведенная на плоскости через основание наклонной перпендикулярно ее проекции,перпендикулярна и самой наклонной.
И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
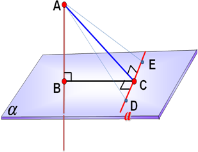 Дано:
Дано:
АВ ┴ α,
АС – наклонная к α
ВС – проекция наклонной АСна α,
а є α, а┴ ВО.
Доказать: а┴ АС
Доказательство:
Откладываем на прямой а произвольные, но равные отрезки СD = СЕ и соединяем отрезками точки А и В с точками D и Е. Тогда имеем: ВD = ВЕ как наклонные к прямой DЕ с равными проекциями СD и СЕ. АD = АЕ как наклонные к плоскости α , которые имеют равные проекции ВD и ВЕ. Следовательно треугольник АDЕ – равнобедренный, значит его медиана АС ┴ к основанию DЕ.
Обратная теорема разбирается устно и предлагается учащимся записать ее доказательство самостоятельно дома.(Слайд 10).
Почему теорема называется теоремой о трех перпендикулярах( в ней говорится про связь между 3 перпендикулярами: АВ ┴ α, а ┴ ВС, а ┴ АС).
ІV. Закрепление нового материала ( 8 мин)
Учитель: Перейдем к решению задач. Не надо бояться пойти по ложному пути, вспомните девиз нашего урока: «Наиболее удобный путь становится известным лишь после того, как мы испробуем все пути».
Решение задачи подразделяется на следующие задания: усвоение условия, продумывание плана, идеи решения, коллективное обсуждение идеи решения, оформление решения.
Задача 1.(Слайд 11).
Верно ли утверждение: «Если из двух различных точек, не принадлежащих плоскости, проведены к ней две равные наклонные, то их проекции тоже равны»?

Ответ: нет
Задача 2. (Слайд 12).
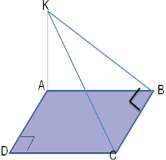 Из вершины А квадрата АВСD восстановлен перпендикуляр АК к его плоскости. Докажите, что ВС перпендикулярно КВ.
Из вершины А квадрата АВСD восстановлен перпендикуляр АК к его плоскости. Докажите, что ВС перпендикулярно КВ.
Дано
АВСD –квадрат.
![]()
Доказать
![]()
Доказательство:

Что и требовалось доказать.
Задача 3.(Слайд 13).
Основание ABCD пирамиды SABCD – прямоугольник, AB <BC. Ребро SD перпендикулярно плоскости основания. Среди отрезков SA, SB, SC и SD укажите наименьший и наибольший.
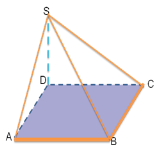
Ответ:SD – наименьший; SB – наибольший.
Самостоятельное выполнение учащимися заданий под контролем учителя.( 14 мин)
1) Учитель демонстрирует тестовые задания, зачитывает условие с экрана. Учащиеся самостоятельно отвечают на вопросы. Для проверки обмениваются тетрадями. ( 5 мин)
Учитель: Ребята, сейчас отвечая на вопросы тестовых заданий, вы должны установить истинность или ложность утверждения, тем самым отметив на таблице соответственно знаками «+» и «-», после чего произведите взаимопроверку, сверяя ответы с образцом. (Слайд 14 -16).
- Верно ли, что две прямые, перпендикулярные к одной плоскости параллельны?
- Может ли прямая, перпендикулярная к плоскости, быть параллельна прямой, лежащей в этой плоскости?
- Верно ли, что прямая перпендикулярна к плоскости, если она перпендикулярна к двум прямым этой плоскости?
- Могут ли две пересекающиеся прямые быть перпендикулярными к одной плоскости?
- Верно ли, что две прямые в пространстве, перпендикулярные к третьей, параллельны?
- Могут ли пересекаться две плоскости, параллельныек одной прямой?
- Верно ли, что длина перпендикуляра меньше длины наклонной, проведенной из той же точки?
|
№ вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Ответ |
+ |
- |
- |
- |
- |
- |
+ |
Критерии оценок за:
7 правильных ответов – 5 баллов,
6 правильных ответов – 4 балла,
5 правильных ответов – 3 балла.
2). Самостоятельное решение задач. ( 9 мин)
Каждому учащемуся раздается карточка с разноуровневыми задачами. Задача 3 уровня на 5 баллов, 2уровня – на 4 балла, 1 уровня – на 3 балла. Каждый выбирает себе уровень сложности и решает задачу, по истечении времени работы сдаются на проверку.
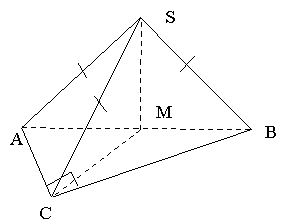
I уровень.
Дано:![]() , АС ┴ ВС,
, АС ┴ ВС,
SA = SB = SC =10 см;
СМ =5 см –медиана.
Найти: SM (расстояние от точки S
до плоскости (АВС).
Решение:
- Прямая SM, М – середина гипотенузы АВ, перпендикулярна к плоскости (АВС) SM ┴ (АВС).
-
SM =
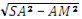 =
=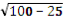 =
= 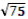 =5
=5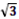 (см).
(см).
Ответ: 5![]() (см).
(см).
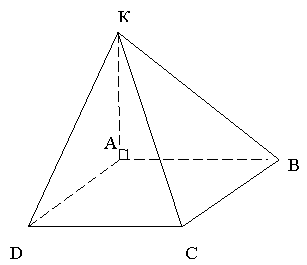
II уровень
Дано: ABCD – прямоугольник;
АК ┴ (АВС), KD= 6 см,
КВ = 7 см, КС = 9 см.
Найти: расстояние от точки К до (АВС).
Решение:
- Длина АК – расстояние от К до (АВС) по определению.
-
Так как DC ┴ AD, AD проекция KD, то по ТТП KD┴DC, значит, в
 KDC . KC2 = KD2 + DC2, DC =
KDC . KC2 = KD2 + DC2, DC = 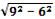 =
= 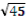 = 3
= 3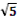 (см).
(см).
-
СВ┴КВ по ТТП; СВ =
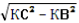 ; СВ = 4
; СВ = 4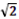 (см).
(см).
-
Из
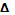 ADC <D = 90º, AC =
ADC <D = 90º, AC = 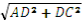 , AC =
, AC = 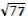 (см).
(см).
-
ИЗ
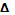 КСА < A = 90º, KA =
КСА < A = 90º, KA = 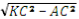 , KA =2 (см).
, KA =2 (см).
Ответ: 2 см.
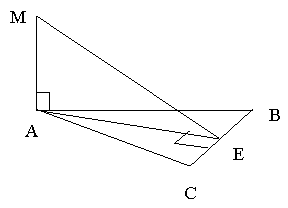
III уровень.
Дано: АВ = 17 см, АС = 15 см,
ВС = 8 см, АМ ┴ (АВС),
<А – меньший, АМ = 20 см.
Найти: МЕ.
Решение:
1.В ![]() АВС против меньшей стороны лежит меньший угол (по теореме синусов). Проведем АЕ ┴ ВС, АЕ ┴ МЕ. По теореме о трех перпендикулярах МЕ ┴ ВС.
АВС против меньшей стороны лежит меньший угол (по теореме синусов). Проведем АЕ ┴ ВС, АЕ ┴ МЕ. По теореме о трех перпендикулярах МЕ ┴ ВС.
2. По формуле Герона:
S![]() =
= ![]() , S
, S![]() =
=![]() BC·AE.
BC·AE.
P = ![]() = 20, S
= 20, S![]() =
=![]() = 60.
= 60.
AE = 15 (см).
По теореме Пифагора: МЕ = ![]() , МЕ = 25 (см).
, МЕ = 25 (см).
Ответ: 25 см.
V. Подведение итогов занятия( 1 мин)
Учитель предлагает обобщить учащимся весь теоретический материал, используемый на уроке. Выставляются оценки за урок.
VI. Домашнее задание. (Слайд 17) ( 3мин)
§ 39, вопросы 1-4, № 246,248,251(1)
Дополнительная задача:
Через сторону АD ромба ABCD проведена плоскость α. Найдите расстояние от прямой ВС до плоскости α, если S ромба = 80 см2, высота равна 8 см, а угол между проекцией стороны CD и прямой AD равен 45º.
И закончить наш урок хочется словами, сказанными Рене Декартом
«Чем труднее доказательство, тем больше будет удовольствия тому ,
кто это доказательство найдет». ( Слайд 18, 19)
Приложение 1
____________________________________________________________________
( ФИО ) класс
Практическая работа.
|
1.Постройте перпендикуляр и наклонную к плоскости листа картона (используя палочки и пластилин). 2.Построите проекцию наклонной на плоскость α.
4.Выскажите предположение о расположении проведённой прямой и проекции наклонной. 5.Проверьте высказанное предположение с помощью модели прямоугольного треугольника. По рисунку запишите: наклонная ____________ перпендикуляр ____________ проекция наклонной на плоскость ________
Запишите символами: как расположена наклонная к прямой а, _________ По вашему предположению как расположена проекция к прямой а.
Выскажите гипотезу.
|
Приложение 2
І.Вопросы тестового задания.
- Верно ли, что две прямые, перпендикулярные к одной плоскости параллельны?
- Может ли прямая, перпендикулярная к плоскости, быть параллельна прямой, лежащей в этой плоскости?
- Верно ли, что прямая перпендикулярна к плоскости, если она перпендикулярна к двум прямым этой плоскости?
- Могут ли две пересекающиеся прямые быть перпендикулярными к одной плоскости?
- Верно ли, что две прямые в пространстве, перпендикулярные к третьей, параллельны?
- Могут ли пересекаться две плоскости, параллельные к одной прямой?
- Верно ли, что длина перпендикуляра меньше длины наклонной, проведенной из той же точки?
|
№ вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Ответ |
|
|
|
|
|
|
|
ІІ. Самостоятельное решение задач
|
I уровень.
Дано: SA = SB = SC =10 см; СМ =5 см –медиана. Найти: SM (расстояние от точки S до плоскости (АВС).
|
II уровень
Дано: ABCD – прямоугольник; АК ┴ (АВС), KD= 6 см, КВ = 7 см, КС = 9 см. Найти: расстояние от точкиК до (АВС).
|
III уровень.
Дано: АВ = 17 см, АС = 15 см, ВС = 8 см, АМ ┴ (АВС), <А – меньший, АМ = 20 см. Найти: МЕ. |
Решение
1


про публікацію авторської розробки
Додати розробку