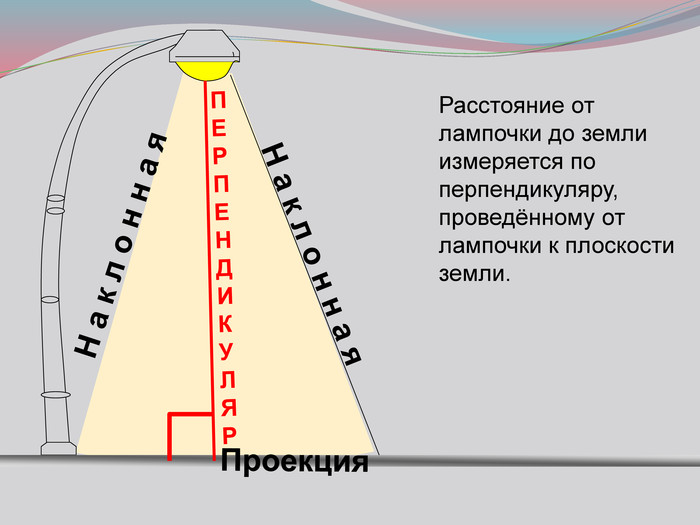
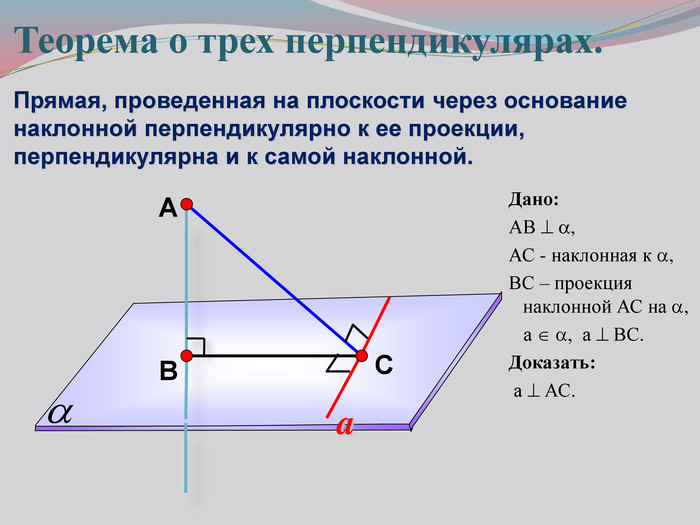
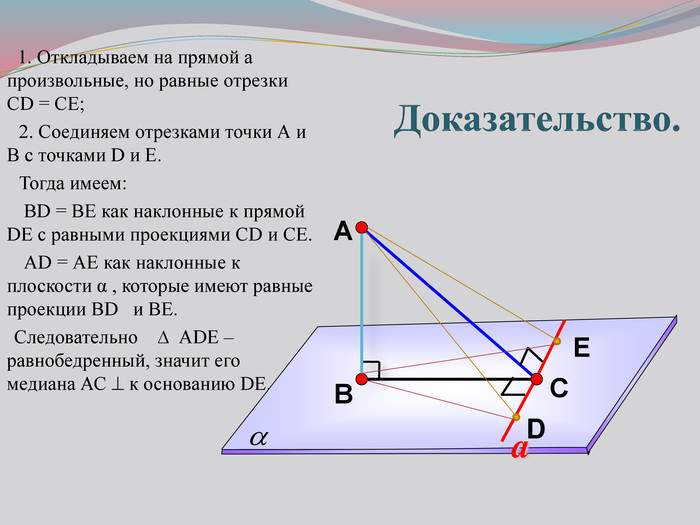
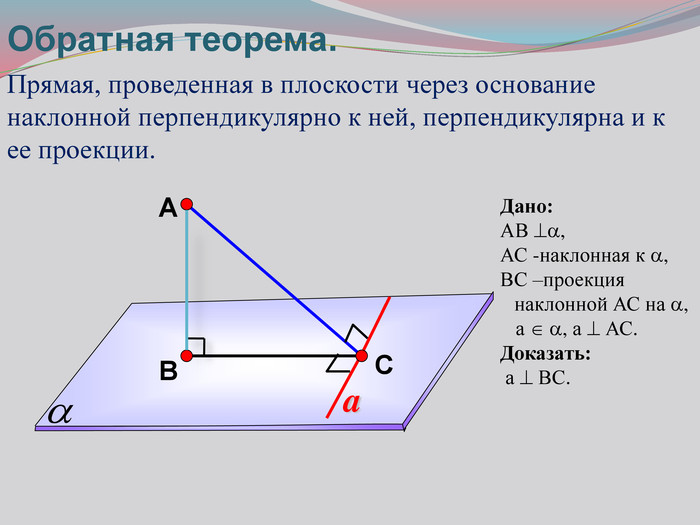
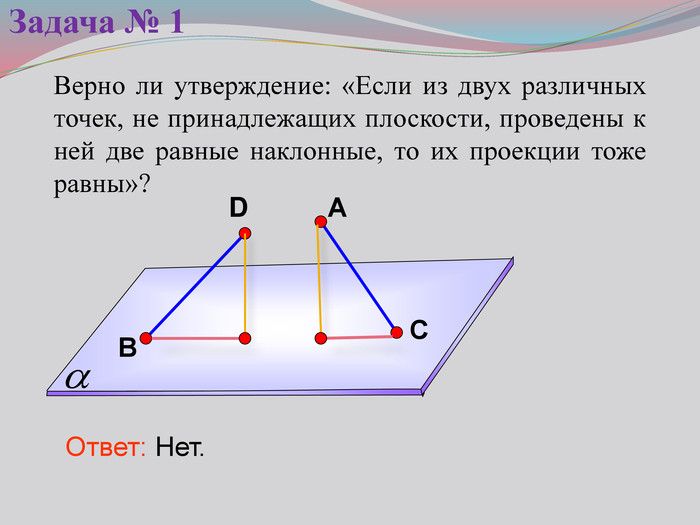
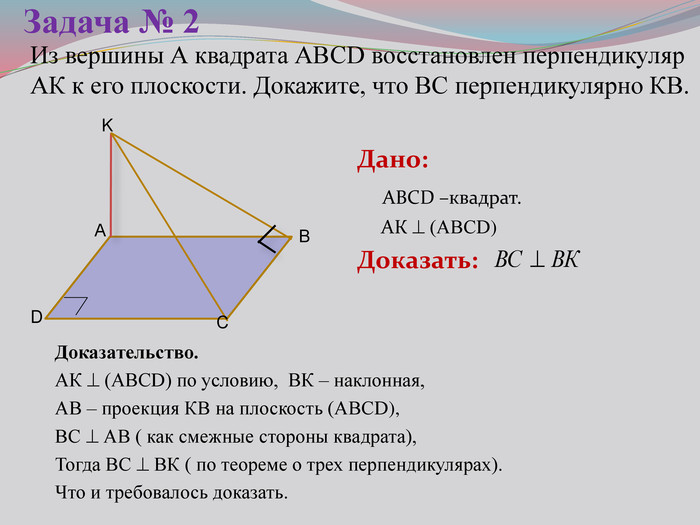
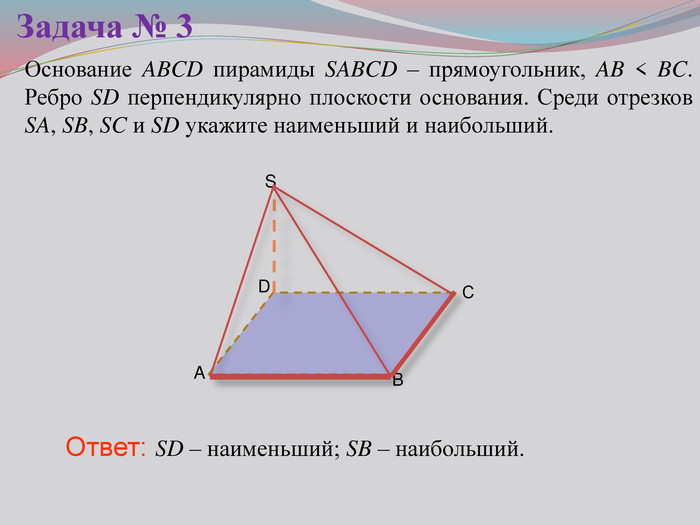
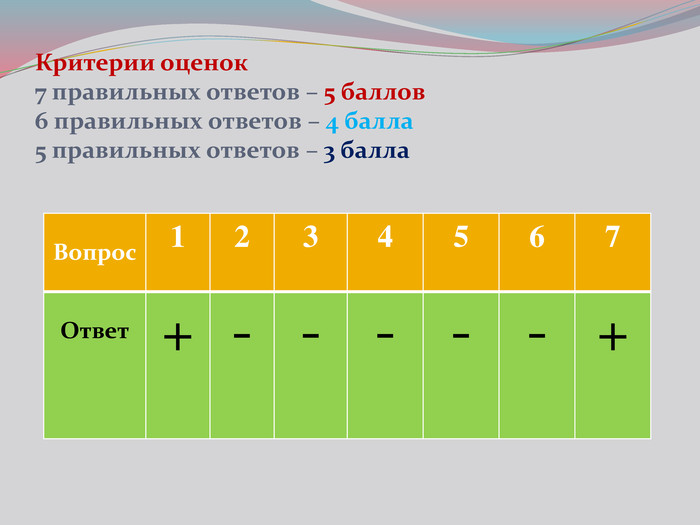
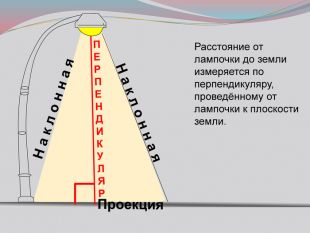
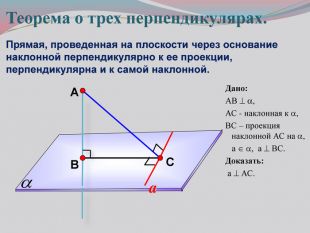
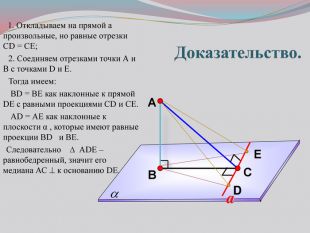
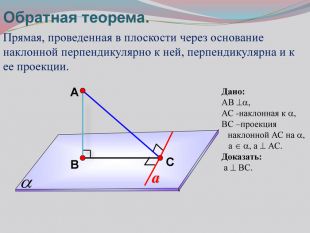
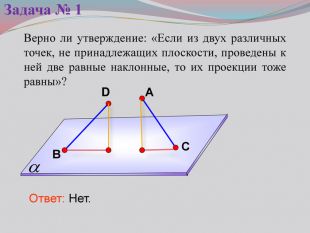
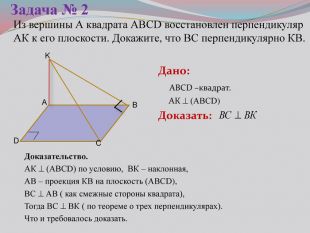
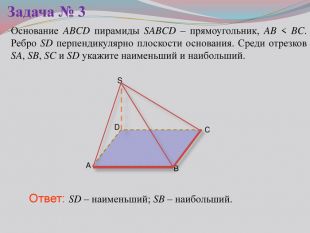
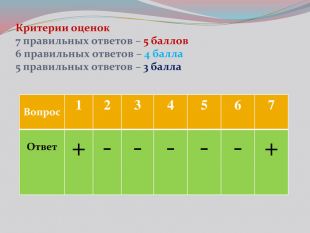
Презентация к уроку на тему: «Теорема о трех перпендикулярах».
Про матеріал
Презентация к уроку на тему: «Теорема о трех перпендикулярах». Урок изучения и первичного закрепления новых знаний. План - конспект уроку выложен на данном сайте. Перегляд файлу
Зміст слайдів
ppt
До підручника
Геометрія (профільний рівень) 10 клас (Бевз В.Г., Бевз Г.П., Владімірова Н.Г., Владіміров В.М.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку