Презентація "Площі бічної та повної поверхонь конуса".

Урок геометрії в групі № 47 ІІІ курсу. Підготувала викладач вищої кваліфікаційної категорії Ющенко Л. Ф

Девіз уроку: Не просто слухати, а чути. Не просто дивитися, а бачити. Не просто розмовляти, а діло творити. Не просто відповідати, а міркувати, Дружно і плідно працювати.

Самостійна робота{16 D9 F66 E-5 EB9-4882-86 FB-DCBF35 E3 C3 E4}12345{16 D9 F66 E-5 EB9-4882-86 FB-DCBF35 E3 C3 E4}67891011121314

1. На якому з малюнків зображено конус? ЛАКМПОЗУ

2-6. Укажіть елементи конуса.{16 D9 F66 E-5 EB9-4882-86 FB-DCBF35 E3 C3 E4}2. SЩТвірна 3. SОІРадіус основи4. SAЛВершина5. ОAКХорда6. SABМАпофема  ПОсьовий переріз  Б:)  ОВисота

7. Що є основою конуса?АОЬЛТУ

8. Яка з даних фігур є осьовий переріз конуса?ПЛВДКС

9. Яке зображення є розгорткою конуса?ОЛСАЕ

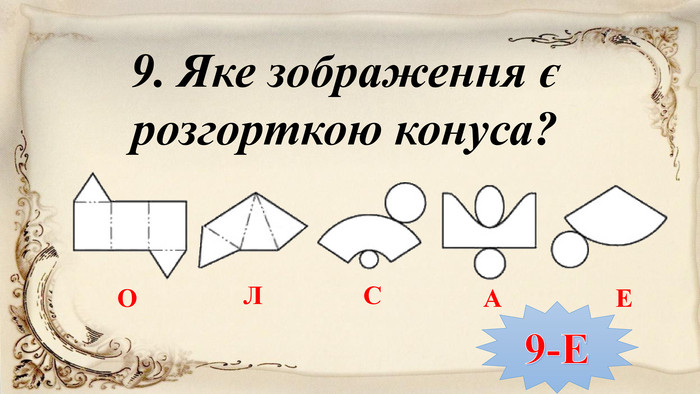
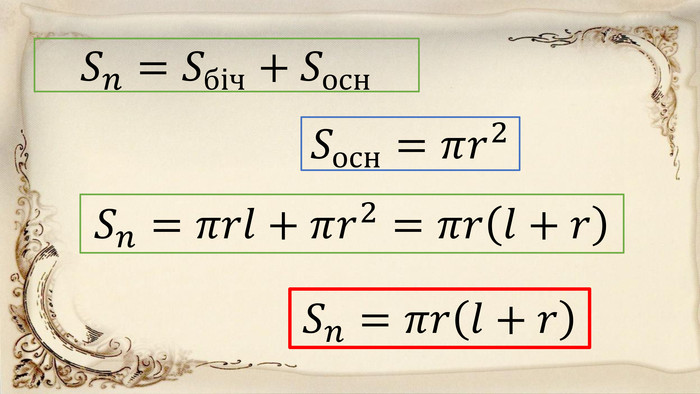
10-14. Установіть відповідність.{16 D9 F66 E-5 EB9-4882-86 FB-DCBF35 E3 C3 E4}10.𝐜𝟐=𝐚𝟐+𝐛𝟐 НРадіус круга11.𝐒=𝛑𝐑𝟐 ПТеорема Вієта12. С=𝟐𝛑𝐫ХПлоща круга13.𝐫=𝐝𝟐 РТеорема Піфагора14.𝐝=𝟐𝐫КЩось гарненьке  ОДовжина кола  ЬДіаметр круга{16 D9 F66 E-5 EB9-4882-86 FB-DCBF35 E3 C3 E4}10. НРадіус круга11. ПТеорема Вієта12. ХПлоща круга13. РТеорема Піфагора14. КЩось гарненьке  ОДовжина кола  ЬДіаметр круга

1. На якому з малюнків зображено конус? ЛАКМПОЗУ1-П

2-6. Укажіть елементи конуса.{16 D9 F66 E-5 EB9-4882-86 FB-DCBF35 E3 C3 E4}2. SЩТвірна 3. SОІРадіус основи4. SAЛВершина5. ОAКХорда6. SABМАпофема  ПОсьовий переріз  Б:)  ОВисота2-Л3-О4-Щ5-І6-П

7. Що є основою конуса?АОЬЛТУ7-О

8. Яка з даних фігур є осьовий переріз конуса?ПЛВДКС8-В

9. Яке зображення є розгорткою конуса?ОЛСАЕ9-Е

10-14. Установіть відповідність.{16 D9 F66 E-5 EB9-4882-86 FB-DCBF35 E3 C3 E4}10.𝐜𝟐=𝐚𝟐+𝐛𝟐 НРадіус круга11.𝐒=𝛑𝐑𝟐 ПТеорема Вієта12. С=𝟐𝛑𝐫ХПлоща круга13.𝐫=𝐝𝟐 РТеорема Піфагора14.𝐝=𝟐𝐫КЩось гарненьке  ОДовжина кола  ЬДіаметр круга{16 D9 F66 E-5 EB9-4882-86 FB-DCBF35 E3 C3 E4}10. НРадіус круга11. ПТеорема Вієта12. ХПлоща круга13. РТеорема Піфагора14. КЩось гарненьке  ОДовжина кола  ЬДіаметр круга10-Р11-Х12-О13-Н14-Ь

Самостійна робота{16 D9 F66 E-5 EB9-4882-86 FB-DCBF35 E3 C3 E4}12345 ПЛОЩІ{16 D9 F66 E-5 EB9-4882-86 FB-DCBF35 E3 C3 E4}67891011121314 ПОВЕРХОНЬ

Площі бічної та повної поверхонь конуса. Мета уроку: домогтися засвоєння формул для обчислення площ бічної та повної поверхонь конуса; сформувати вміння розв’язувати задачі, що передбачають застосування формул для обчислення площ бічної та повної поверхонь конуса.

Конусоподібну палатку висотою 2,4 м і діаметром основи 1,4 м вкрито тканиною. Скільки квадратних метрів тканини пішло на палатку?Задача 1

Площа бічної поверхні конуса у скільки разів менша від площі круга радіуса 𝒍, у скільки разів 𝟐𝝅𝒓 менше від 𝟐𝝅𝒍. Тому 𝑺біч:𝝅𝒍𝟐=𝟐𝝅𝒓:𝟐𝝅𝒍, звідки 𝑺біч=𝝅𝒓𝒍 

𝑆𝑛=𝑆біч+𝑆осн 𝑆осн=𝜋𝑟2 𝑆𝑛=𝜋𝑟𝑙+𝜋𝑟2=𝜋𝑟𝑙+𝑟 𝑆𝑛=𝜋𝑟𝑙+𝑟 

Конусоподібну палатку висотою 2,4 м і діаметром основи 1,4 м вкрито тканиною. Скільки квадратних метрів тканини пішло на палатку?Задача 1

Конусоподібну палатку висотою 2,4 м і діаметром основи 1,4 м вкрито тканиною. Скільки квадратних метрів тканини пішло на палатку?Задача 1 Розв'язування Які елементи конуса вам відомі?Висота та діаметр. Що необхідно знайти?Площу бічної поверхніЗа допомогою якої формули знайдемо площу бічної поверхні конуса?𝑺біч=𝝅𝒓𝒍 Побудуйте малюнок.

Чому дорівнює радіус конуса?𝒓= 𝟏𝟐 𝒅 Як знайти твірну конуса? за теоремою Піфагора. Знайдіть твірну конуса. Із трикутника SOA (∠ SOA = 90°) отримаємо за теоремою Піфагора: ℓ = SA = 𝑺𝑶𝟐+𝑶𝑨𝟐, ℓ = 𝟓,𝟕𝟔+𝟎, 𝟒𝟗 = 𝟔,𝟐𝟓=𝟐,𝟓 м. Знайдіть бічну поверхню конуса. 𝐒біч=𝛑𝒓𝓵, тоді 𝐒біч=𝟑,𝟏𝟒·𝟎,𝟕·𝟐,𝟓≈𝟓,𝟒𝟗𝟓 м𝟐. Запишіть відповідь. Відповідь: ≈ 5,495 м𝟐. 

Трубочки мають форму конуса. Яким буде діаметр цього конуса, якщо довжина трубочки (твірна конуса) – 14 см, і твірна нахилена до основи під кутом  60º? Скільки потрібно матеріалу, щоб обгорнути одну трубочку повністю (конус), якщо шви і відходи не враховувати? Задача 2 Запишіть коротко умову задачі. Запишіть формулу для обчислення площі повної поверхні конуса. Чому дорівнює кут між твірною та висотою конуса?Знайдіть радіус конуса, використовуючи властивість прямокутного трикутника з кутом 30°. Знайдіть Sп Яким буде діаметр даного конуса?Запишіть відповідь.

Запишіть коротко умову задачі. Дано: 𝒍=𝑺𝑨=𝟏𝟒см;∠𝑺𝑨𝑶=𝟔𝟎°. 𝑺𝒏−?  Запишіть формулу для обчислення площі повної поверхні конуса. Sп = π𝒓 (ℓ+𝒓),  Чому дорівнює кут між твірною та висотою конуса? Із трикутника 𝑺𝑶𝑨:∠𝑺𝑶𝑨=𝟗𝟎°,∠𝑺𝑨𝑶=𝟔𝟎° (за умовою), тоді ∠𝑨𝑺𝑶=𝟑𝟎°.  Знайдіть радіус конуса, використовуючи властивість прямокутного трикутника з кутом 𝟑𝟎°. 𝒓=𝟏𝟐𝒍=𝟏𝟒:𝟐=𝟕 см Знайдіть Sп 𝑺𝒏=𝝅∙𝟕𝟏𝟒+𝟕=𝟏𝟒𝟕𝝅 =𝟏𝟒𝟕∙𝟑,𝟏𝟒≈𝟒𝟔𝟐 см𝟐 Яким буде діаметр даного конуса?𝑨𝑩=𝒅=𝟐𝑹=𝟏𝟒 см Запишіть відповідь. Відповідь: ≈𝟒𝟔𝟐 см𝟐, 𝟏𝟒 см  

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA- … = 2 см; ∠… = 60° . Знайти: … - ?Розв’язок: Із трикутника SOA : ∠ SOA = … , ∠ … = 60° (за умовою), тоді ∠ … = 30°, тобто …= 12𝑆𝐴; тоді SA - 12 SA= … , SA=4 см. Отже SO= 12 SA= … см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−…2=16−… =12=23 (см). Відомо, що 𝑆б.п=𝜋…𝑙,  тоді 𝑆б.п=𝜋…4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠… = 60° . Знайти: … - ?Розв’язок: Із трикутника SOA : ∠ SOA = … , ∠ … = 60° (за умовою), тоді ∠ … = 30°, тобто …= 12𝑆𝐴; тоді SA - 12 SA= … , SA=4 см. Отже SO= 12 SA= … см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−…2=16−… =12=23 (см). Відомо, що 𝑆б.п=𝜋…𝑙,  тоді 𝑆б.п=𝜋…4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: … - ?Розв’язок: Із трикутника SOA : ∠ SOA = … , ∠ … = 60° (за умовою), тоді ∠ … = 30°, тобто …= 12𝑆𝐴; тоді SA - 12 SA= … , SA=4 см. Отже SO= 12 SA= … см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−…2=16−… =12=23 (см). Відомо, що 𝑆б.п=𝜋…𝑙,  тоді 𝑆б.п=𝜋…4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: 𝑺б - ?Розв’язок: Із трикутника SOA : ∠ SOA = … , ∠ … = 60° (за умовою), тоді ∠ … = 30°, тобто …= 12𝑆𝐴; тоді SA - 12 SA= … , SA=4 см. Отже SO= 12 SA= … см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−…2=16−… =12=23 (см). Відомо, що 𝑆б.п=𝜋…𝑙,  тоді 𝑆б.п=𝜋…4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: 𝑺б - ?Розв’язок: Із трикутника SOA : ∠ SOA = 90°, ∠ … = 60° (за умовою), тоді ∠ … = 30°, тобто …= 12𝑆𝐴; тоді SA - 12 SA= … , SA=4 см. Отже SO= 12 SA= … см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−…2=16−… =12=23 (см). Відомо, що 𝑆б.п=𝜋…𝑙,  тоді 𝑆б.п=𝜋…4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: 𝑺б - ?Розв’язок: Із трикутника SOA : ∠ SOA = 90°, ∠ ASO = 60° (за умовою), тоді ∠ … = 30°, тобто …= 12𝑆𝐴; тоді SA - 12 SA= … , SA=4 см. Отже SO= 12 SA= … см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−…2=16−… =12=23 (см). Відомо, що 𝑆б.п=𝜋…𝑙,  тоді 𝑆б.п=𝜋…4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: 𝑺б - ?Розв’язок: Із трикутника SOA : ∠ SOA = 90°, ∠ ASO = 60° (за умовою), тоді ∠ 𝑺𝑨𝑶 = 30°, тобто …= 12𝑆𝐴; тоді SA - 12 SA= … , SA=4 см. Отже SO = 12 SA = … см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−…2=16−… =12=23 (см). Відомо, що 𝑆б.п=𝜋…𝑙,  тоді 𝑆б.п=𝜋…4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: 𝑺б - ?Розв’язок: Із трикутника SOA : ∠ SOA = 90°, ∠ ASO = 60° (за умовою), тоді ∠ 𝑺𝑨𝑶 = 30°, тобто 𝑺𝑶=12𝑆𝐴 ; тоді SA - 12 SA= … , SA=4 см. Отже SO = 12 SA = … см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−…2=16−… =12=23 (см). Відомо, що 𝑆б.п=𝜋…𝑙,  тоді 𝑆б.п=𝜋…4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: 𝑺б - ?Розв’язок: Із трикутника SOA : ∠ SOA = 90°, ∠ ASO = 60° (за умовою), тоді ∠ 𝑺𝑨𝑶 = 30°, тобто 𝑺𝑶=12𝑆𝐴 ; тоді SA - 12 SA= 2 , SA=4 см. Отже SO = 12 SA = … см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−…2=16−… =12=23 (см). Відомо, що 𝑆б.п=𝜋…𝑙,  тоді 𝑆б.п=𝜋…4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: 𝑺б - ?Розв’язок: Із трикутника SOA : ∠ SOA = 90°, ∠ ASO = 60° (за умовою), тоді ∠ 𝑺𝑨𝑶 = 30°, тобто 𝑺𝑶=12𝑆𝐴 ; тоді SA - 12 SA= 2 , SA=4 см. Отже SO = 12 SA = 2 см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−…2=16−… =12=23 (см). Відомо, що 𝑆б.п=𝜋…𝑙,  тоді 𝑆б.п=𝜋…4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: 𝑺б - ?Розв’язок: Із трикутника SOA : ∠ SOA = 90°, ∠ ASO = 60° (за умовою), тоді ∠ 𝑺𝑨𝑶 = 30°, тобто 𝑺𝑶=12𝑆𝐴 ; тоді SA - 12 SA= 2 , SA=4 см. Отже SO = 12 SA = 2 см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−𝑺𝑶2=16−… =12=23 (см). Відомо, що 𝑆б.п=𝜋…𝑙,  тоді 𝑆б.п=𝜋…4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: 𝑺б - ?Розв’язок: Із трикутника SOA : ∠ SOA = 90°, ∠ ASO = 60° (за умовою), тоді ∠ 𝑺𝑨𝑶 = 30°, тобто 𝑺𝑶=12𝑆𝐴 ; тоді SA - 12 SA= 2 , SA=4 см. Отже SO = 12 SA = 2 см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−𝑺𝑶2=16−𝟒 =12=23 (см). Відомо, що 𝑆б.п=𝜋…𝑙,  тоді 𝑆б.п=𝜋…4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: 𝑺б - ?Розв’язок: Із трикутника SOA : ∠ SOA = 90°, ∠ ASO = 60° (за умовою), тоді ∠ 𝑺𝑨𝑶 = 30°, тобто 𝑺𝑶=12𝑆𝐴 ; тоді SA - 12 SA= 2 , SA=4 см. Отже SO = 12 SA = 2 см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−𝑺𝑶2=16−𝟒 =12=23 (см). Відомо, що 𝑆б.п=𝜋𝒓𝑙,  тоді 𝑆б.п=𝜋…4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: 𝑺б - ?Розв’язок: Із трикутника SOA : ∠ SOA = 90°, ∠ ASO = 60° (за умовою), тоді ∠ 𝑺𝑨𝑶 = 30°, тобто 𝑺𝑶=12𝑆𝐴 ; тоді SA - 12 SA= 2 , SA=4 см. Отже SO = 12 SA = 2 см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−𝑺𝑶2=16−𝟒 =12=23 (см). Відомо, що 𝑆б.п=𝜋𝒓𝑙,  тоді 𝑆б.п=𝜋∙𝟐𝟑∙4= …3𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: 𝑺б - ?Розв’язок: Із трикутника SOA : ∠ SOA = 90°, ∠ ASO = 60° (за умовою), тоді ∠ 𝑺𝑨𝑶 = 30°, тобто 𝑺𝑶=12𝑆𝐴 ; тоді SA - 12 SA= 2 , SA=4 см. Отже SO = 12 SA = 2 см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−𝑺𝑶2=16−𝟒 =12=23 (см). Відомо, що 𝑆б.п=𝜋𝒓𝑙,  тоді 𝑆б.п=𝜋∙𝟐𝟑∙4= 83𝜋 см2 Відповідь: … . 

Розв’яжіть задачу № 789, заповнив пропуски. Дано: конус; SA-  𝑺𝟎  = 2 см; ∠ASO = 60° . Знайти: 𝑺б - ?Розв’язок: Із трикутника SOA : ∠ SOA = 90°, ∠ ASO = 60° (за умовою), тоді ∠ 𝑺𝑨𝑶 = 30°, тобто 𝑺𝑶=12𝑆𝐴 ; тоді SA - 12 SA= 2 , SA=4 см. Отже SO = 12 SA = 2 см. За теоремою Піфагора: 𝐴𝑂=𝑆𝐴2−𝑺𝑶2=16−𝟒 =12=23 (см). Відомо, що 𝑆б.п=𝜋𝒓𝑙,  тоді 𝑆б.п=𝜋∙𝟐𝟑∙4= 83𝜋 см2 Відповідь: 8𝟑𝝅 см𝟐. 

Домашнє завдання Г. П. Бевз «Математика 11 клас». § 21 сторінка 191 Розв’язати вправи № 788, № 803(а). Практичне додаткове завдання. 

Дякую за урок!!!