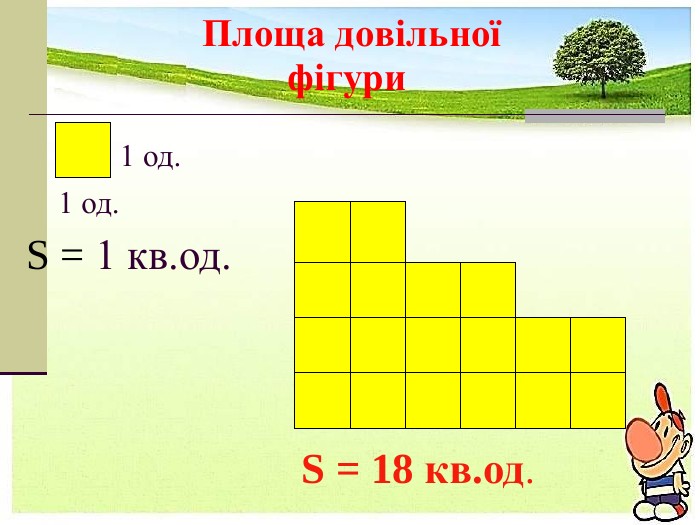
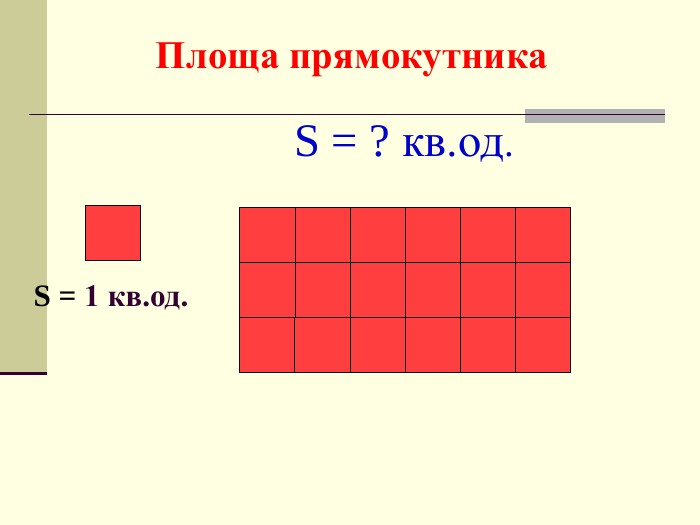
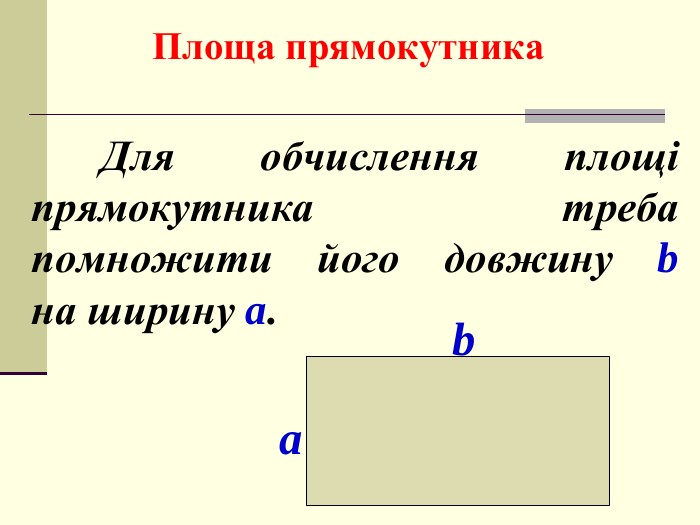
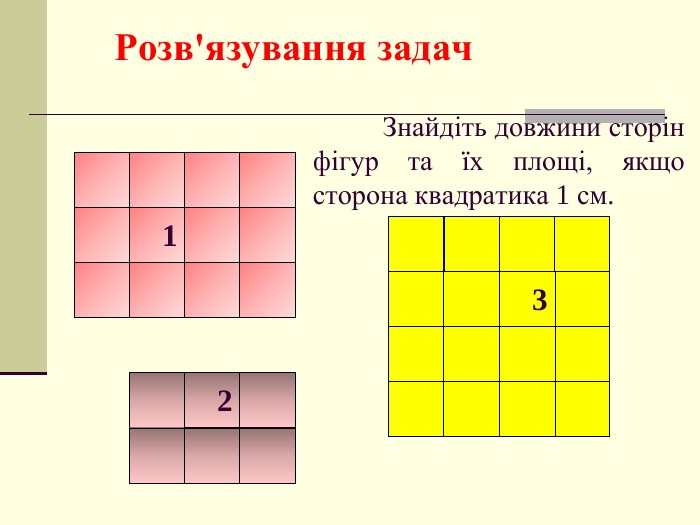
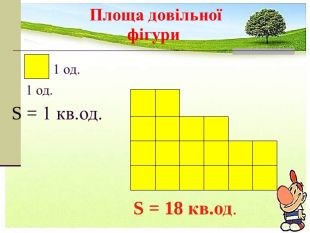
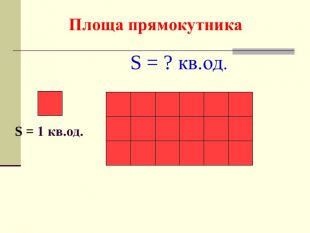
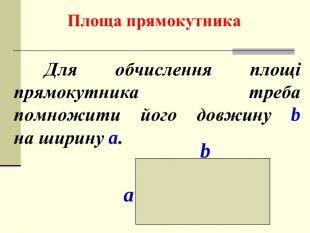
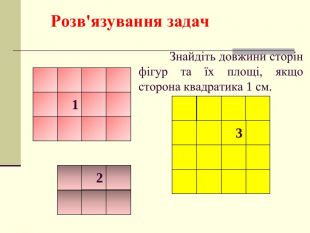
Презентація. площі многокутника. Площа прямокутника.

Будуємо фундамент будиночку знань

ТЕМА: ПОНЯТТЯ ПЛОЩІ МНОГОКУТНИКА. ПЛОЩА ПРЯМОКУТНИКА. МЕТА: ВВЕСТИ ПОНЯТТЯ «ПЛОЩА МНОГОКУТНИКА», РОЗГЛЯНУТИ ВЛАСТИВОСТІ ПЛОЩІ МНОГОКУТНИКА; ФОРМУВАТИ ВМІННЯ ВИЗНАЧАТИ ПЛОЩУ ПРЯМОКУТНИКА Й КВАДРАТА ПРИ РОЗВ’ЯЗАННІ ЗАДАЧ.

1. РІВНІ МНОГОКУТНИКИ МАЮТЬ РІВНІ ПЛОЩІ; 2. ЯКЩО МНОГОКУТНИК СКЛАДЕНО З КІЛЬКОХ МНОГОКУТНИКІВ, ТО ЙОГО ПЛОЩА ДОРІВНЮЄ СУМІ ПЛОЩ ЦИХ МНОГОКУТНИКІВ; 3. ЗА ОДИНИЦЮ ВИМІРУ ПЛОЩІ БЕРУТЬ ОДИНИЧНИЙ КВАДРАТ, ТОБТО КВАДРАТ ЗІ СТОРОНОЮ, ЯКА ДОРІВНЮЄ ОДИНИЦІ ВИМІРУ ДОВЖИНИ. Означення Площею многокутника називають додатну величину, яка має такі властивості

1 од. S = 18 кв.од. S = 1 кв.од. 1 од. Площа довільної фігури

S = ? кв.од. S = 1 кв.од. Площа прямокутника

Для обчислення площі прямокутника треба помножити його довжину b на ширину a. a b Площа прямокутника

Якщо позначити сторони прямокутника через a і b, а площу - S, то дістанемо формулу площі прямокутника: Площа прямокутника

Квадрат – це прямокутник, у якого всі сторони рівні. Тоді формулу площі квадрата S зі стороною а можна записати так: S = a·а або Площа квадрата

Одиниці вимірювання площ 1 дм2=100 см2 1 см2= 10мм Ч10 мм=100 мм2 1 м2 =100 дм2 =10000 см2 1 км2 = 1000 м · 1000 м = 1000000 м2

Одиниці вимірювання площ 603 700 км2

Одиниці вимірювання площ 1 а = 10 м · 10 м = 100 м2 1 га = 100 а = 100 · 100 м2 = 10 000 м2 1 км2 =100 га

Літера S, якою позначають площу в математиці це перша літера латинського слова superficies – поверхня. З історії виникнення слів Ар - від латинського слова area – площа. Гектар - від грецького слова hekaton - сто.

Означення Многокутники, які мають рівні площі, називають рівновеликими.

Знайдіть довжини сторін фігур та їх площі, якщо сторона квадратика 1 см. 1 2 3 Розв'язування задач

Дванадцять зі ста незвичайних будинків світу

Кривий будинок. Сопот. Польща

Лісова спіраль. Дармштадт. Німеччина

Хабітат 67. Монреаль. Канада

Кубічні будинки. Роттердам. Нідерланди

Танцюючий будинок. Прага. Чехія

Будинок-чайник. Техас. США

Сюрреалістичний будинок. Барселона. Іспанія

Будинок-камінь. Гюемараєс. Португалія

Будинок-черевик. Пенсільванія. Америка

Будинок-човен. Керала. Індія

Будинок-сфера для вільних духом. Куалікум Біч. Британська Колумбія. Канада

Геліотропний будинок, що обертається. Фрайбург. Німеччина

Підсумки уроку Чи правильним є твердження? Якщо дві фігури рівні, то їх площі рівні. Якщо площі двох фігур рівні, то ці фігури рівні. Якщо два квадрати мають рівні площі, то вони рівні. Якщо два прямокутники мають рівні периметри, то їх площі рівні.