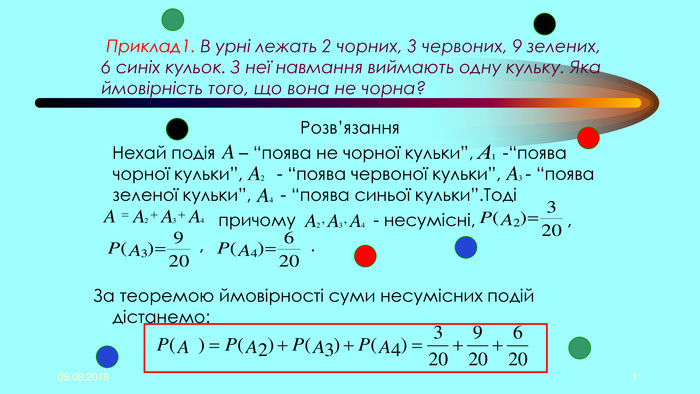
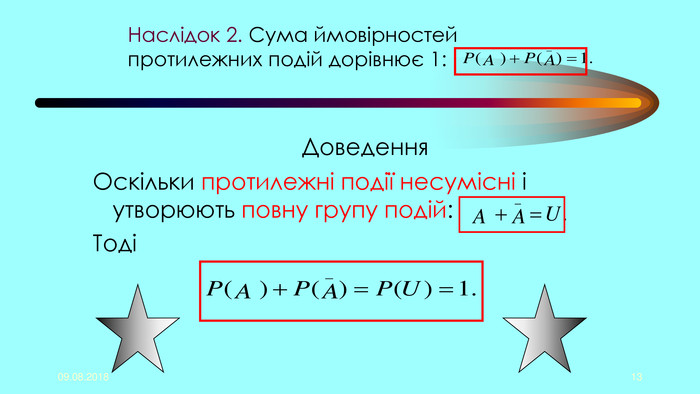
Презентація "Початки теорії ймовірностей. Урок 4, 5,6."
Про матеріал
Презентація складається з уроків №4, № 5, №6, які входять др циклу уроків з теми «Елементи теорії ймовірностей» для учнів 11 класу . Матеріал може бути використаний вчителем при підготовці до уроку в повному обсязі чи в скороченому вигляді, залежно від рівня викладання предмету; учнями- при повторенні теми, самостійному вивченні.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра (академічний, профільний рівень) 11 клас (Нелін Є.П., Долгова О.Є.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку