Довідковий матеріал до теми "Многокутники. Площі многокутників"

ГЕОМЕТРІЯ, 8   ТЕМА 4.  М Н О Г О К У Т Н И К И.  П Л О Щ І  М Н О Г О К У Т Н И К І В

Опуклий многокутник                                                                                                       Неопуклий многокутник

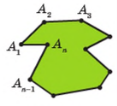
Точки A₁, A₂, ..., A_n-1,  A_n – вершини; відрізки A₁A₂, A₂A₃, … , A_nA₁  – сторони; P = A₁A₂ + A₂A₃ + … + A_nA₁.

Теорема. Сума кутів опуклого многокутника дорівнює 180(n – 2), де n – кількість сторін многокутника

Означення. Многокутник називають вписаним у коло,

                       якщо всі його вершини лежать на колі.

Означення. Многокутник називають описаним навколо
кола, якщо всі його сторони дотикаються до цього кола.

Площа многокутника – це додатна величина, яка має такі властивості:

1. рівні многокутники мають рівні площі;
2. якщо многокутник розбито на кілька многокутників,
   то його площа дорівнює сумі площ цих многокутників;
3. одиницею вимірювання є площа квадрата зі стороною, що дорівнює одиниці довжини.

Теорема. Площа прямокутника                                     Теорема. Площа паралелограма дорівнює добутку

дорівнює добутку його сусідніх сторін.                        його сторони на висоту, проведену до цієї сторони.

                    S = ab                                        S = a²                                        S =                      S = ah_a

           a = R, S = 2R²                   S = , d = a                   h = 2r, S = 2ar                              a = 2r, S = 4r²

Теорема. Площа трапеції дорівнює                    Теорема. Площа трикутника дорівнює половині добутку

добутку півсуми її основ на висоту.                      його сторони на висоту, проведену до цієї сторони.

                        S =                                   S =                             S =                            S =

  S = і S = тому                                   S = pr, де         S_ACM = S_BCM