Презентація. "Повторення. Розв'язування нерівностей"

Повторення. Розв’язування нерівностей

При діленні (множенні) нерівності на від’ємне число – ВСІ знаки змінюються на

протилежні

Якщо нерівність сторога (< або >), то для запису відповіді використовуємо «круглі»

дужки «)» або «(«.

Якщо нерівність нестрога ( ≤ або ≥ ), то для запису відповіді використовуємо

«квадратні» дужки «[« або «]»

•       Розв’яжіть нерівність: 10 − 3𝑥 > 4;

•       −3𝑥 > −6;

•       Ділимо на −3. Знаки змінюються на протилежні.

•       𝑥 < 2

•       Відповідь(−∞;2)

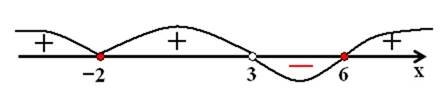
Скористаємось методом інтервалів. х≠ 3, нулі функції: х=-2, х=6.

1.    Розв’яжіть нерівність:

0,2𝑥 − 54 < 0; • 0,2𝑥 < 54 ȁ: 0,2

•        𝑥 < 270.

•        Відповідь:(−∞; 270).

•        Відповідь: {−2} ∪ (3; 6].

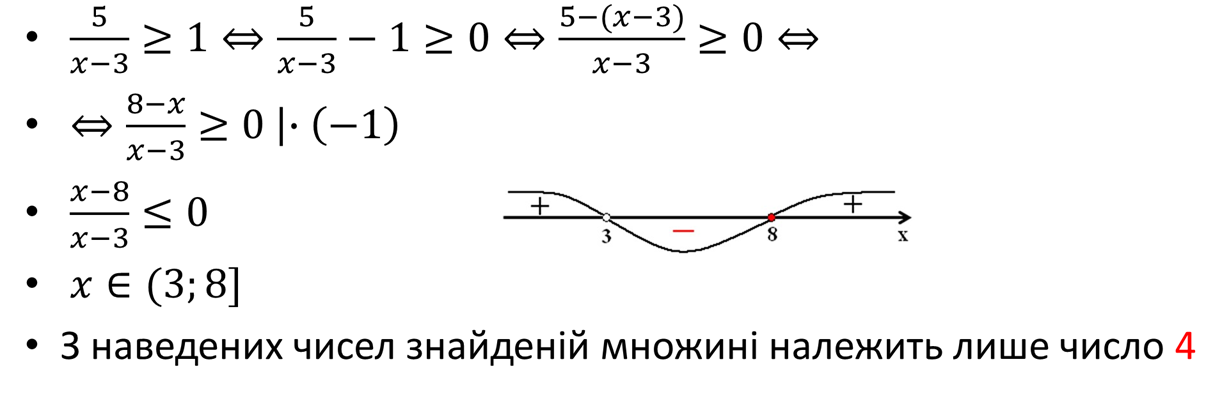
Серед чисел -2, 0, 2, 9, 4 укажіть число, що є розв’язком нерівності.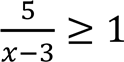

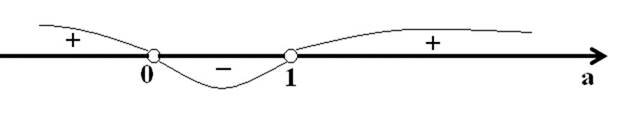Розв’яжіть нерівність:

𝑥 > −2; 𝑥 ≠ 3 ⇒ 𝑥 ∈ (−2; 3) ∪ (3; ∞).

Відповідь: 𝑥 ∈ (−2;3) ∪ (3;∞).

Знайдіть область визначення функції:

𝑦 =       𝑥 + 9

𝑥 + 9 ≥ 0; 𝑥 ≥ −9. Відповідь: х∈ −9; ∞.

.

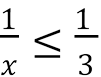•        Розв’яжіть нерівність:

•

•        .

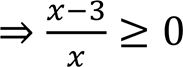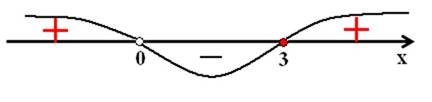
•        Відповідь:−∞; 0 ∪ [3; ∞).

•

•       

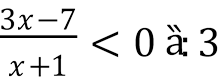
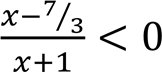•        Відповідь:  .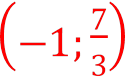

Розв’яжіть нерівність:

(𝑥+4)(𝑥−7)>3(𝑥−7)

•        Помилка (!!!): скоротити на

•

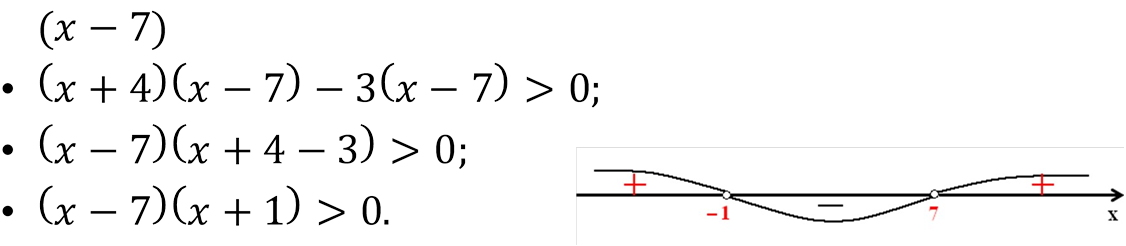
•        Відповідь: (−∞;−1) ∪ (7;∞)

Розв’яжіть нерівність 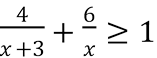. У відповідь запишіть суму цілих розв’язків.

•

•

•        ;

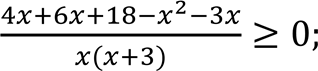
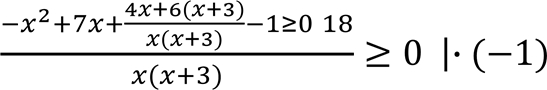
𝑥(𝑥+3)

•

𝑥² − 7𝑥 − 18 = 0;

•        𝐷 = 49 − 4 ∙ −18 = 121;

•        ;

•        ;

•         ;

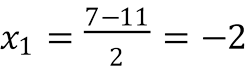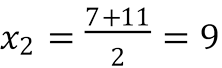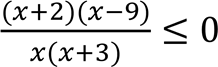•        𝑥 ∈ (−3; −2] ∪ (0; 9].

•        .

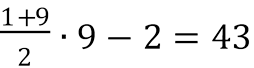•        Відповідь: 4.