Підсумкова контрольна робота з математики, 11 клас.
Підсумкова контрольна робота з математики
11 клас.
Варіант 1
Частина перша
Оберіть правильну відповідь.
- Яка з функцій показникова?
|
А) |
Б) |
В) |
Г) |
|
|
|
|
|
-
Обчислити значення виразу
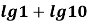 .
.
|
А) |
Б) |
В) |
Г) |
|
11 |
1 |
10 |
|
- Якщо радіус кулі дорівнює 15 см, а точка А знаходиться від центра кулі на відстані 20 см, то точка А лежить:
|
А) |
Б) |
В) |
Г) |
|
всередині кулі |
на поверхні кулі |
поза кулею |
визначити неможливо |
- Якщо висота конуса дорівнює 3 см, а діаметр основи — 8 см, то площа бічної поверхні конуса дорівнює:
|
А) |
Б) |
В) |
Г) |
|
24π см |
20π см2 |
15π см2 |
12π см2 |
-
Знайдіть загальний вигляд первісних для функцій

|
А) |
Б) |
В) |
Г) |
|
|
|
|
|
Частина друга
Розв’язати завдання 6 – 8 з повним поясненням:
-
Знайти корені рівняння
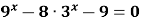 .
.
- Основою піраміди є рівнобедрений трикутник, у якого основа і висота дорівнюють по 8 см. Всі бічні ребра нахилені до основи під кутом 45°. Знайдіть бічне ребро.
- Обчисліть площу фігури, обмеженої лініями
![]()
Варіант 2
Частина перша
Оберіть правильну відповідь.
- Яка з поданих функцій показникова ?
|
А) |
Б) |
В) |
Г) |
|
|
|
|
|
-
Розв’язати рівняння
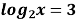 .
.
|
А) |
Б) |
В) |
Г) |
|
2 |
1 |
8 |
9 |
- Якщо радіус кулі дорівнює 15 см, а точка А знаходиться від центра кулі на відстані 10 см, то точка А лежить:
|
А) |
Б) |
В) |
Г) |
|
поза кулею |
на поверхні кулі |
всередині кулі |
визначити неможливо |
- Якщо виміри прямокутного паралелепіпеда дорівнюють 8 см, 9 см і 12 см, то його діагональ дорівнює:
|
А) |
Б) |
В) |
Г) |
|
12 см |
17 см |
20 см |
29 см |
-
Знайдіть невизначений інтеграл
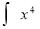 dx
dx
|
А) |
Б) |
В) |
Г) |
|
|
|
|
|
Частина друга
Розв’язати завдання 6 – 8 з повним поясненням:
-
Розв’язати рівняння
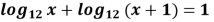 .
.
-
Площа осьового перерізу циліндра дорівнює
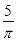 см2. Знайдіть площу бічної поверхні циліндра.
см2. Знайдіть площу бічної поверхні циліндра.
-
Обчисліть площу фігури, обмеженої лініями
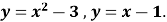


про публікацію авторської розробки
Додати розробку

-

Дідух Оксана
07.04.2025 в 01:49
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мисік Марина Олександрівна
20.12.2024 в 08:06
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Руденко Валентина Олександрівна
02.06.2022 в 09:03
Дякую, корисний матеріал!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Марченко Світлана
24.05.2022 в 13:41
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Доліч Наталія
15.05.2021 в 22:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Доліч Наталія
15.05.2021 в 22:51
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

лена Елена
14.12.2020 в 09:28
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 4 відгука