Любить - не любить(диф. рівняння)

Любить – не любить «Весною, - писав Тенісон, - уява молодої людини з легкістю повертається до думок про любов». Утім, потенційний партнер молодої людини може мати власні уявлення про любов, і тоді їх стосунки будуть повні бурхливих підйомів та падінь, які роблять любов такою зворушливою та такою болісною. Одні, хто страждають від любові без відповіді, шукають пояснення цих любовних гойдалок у вині, інші – у поезії. А ми проконсультуємось у обчислюваннях. Представлений нижче аналіз буде глузливо-іронічним, проте від зачіпає серйозні теми. До того ж якщо розуміння законів кохання може від нас вислизнути, то закони недуховного світу в теперішньому часі гарно вивчені. Вони набувають форми диференційних рівнянь, які описують зміни взаємно пов’язаних змінних від моменту залежності до теперішніх значень. Можливо, у таких рівняннях мало спільного з романтикою, проте вони можеть привідкрити завісу на те, чому, за словами іншого поета, «шлях справжнього кохання ніколи не буває гладким». 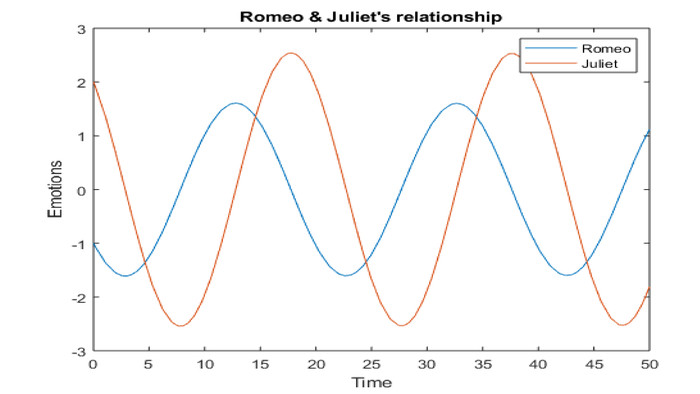[slide 3]Для того щоб продемонструвати метод диференційних рівнянь, припустимо, що Ромео любить Джульєту, проте в нашій версії цієї історії Джульєта – вітряна кохана.(102) Чим більше Ромео кохає її, тим сильніше вона хоче від нього сховатись. Але коли Ромео охолоджує свої почуття до неї, він здається їй надзвичайно привабливим. Однак юний закоханий схильний відбивати її почуття: він палає, коли вона його любить, і охолоджується, коли вона його ненавидить.[ромео – горить, вона холодна і навпаки] Що відбувається з нашими нещасними закоханими? Як любов їх поглинає та йде з плином часу? Ось де диференційні рівняння до нас приходять на допомогу.[даша-подорожувальниця] Склавши рівняння, узагальнивши посилення та послаблення почуттів Ромео та Джульєти, а потім вирішивши їх, ми зможемо передбачити хід стосунків цієї пари. Остаточним прогнозом для неї буде трагічно-нескінченний цикл любові та ненависті. Принаймні четвертина цього часу буде у них взаємним коханням. Для того аби прийти до цього висновку, я припустив, що поведінка Ромео може бути змодельована за допомогою рівняння dR/dt=aJ , яке описує, як його любов (R) змінюється в наступний момент (dt). Згідно з цим рівнянням, кількість змін (dR) прямо пропорційна (з коефіціентом пропорційності а) любові Джульєти(J). Дана залежність відображає те, що ми вже знаємо: кохання Ромео посилюється, коли Джульєта кохає його, проте це також говорить, що любов Ромео зростає прямо пропорційно тому, наскільки Джульєта його кохає. Це припущення лінійної залежності емоційно неправдоподібне, але воно дозволяє значно спростити розв’язання рівняння. Навпаки, поведінка Джульєти можна змоделювати за допомогою рівняння dJ/dt=-bR Від’ємний знак перед змінною b відображає те, що її кохання холоне, коли любов Ромео посилюється. Єдине, що залишилось визначити, - їх початкові почуття(тобто значення J та R у момент часу t=0). Після всього цього усі необхідні параметри будуть задані. Ми можемо використати комп’ютер, щоб повільно, крок за кроком рухатись вперед, змінюючи значення R та J у відповідності до описаних вище диференційних рівнянь. Насправді за допомогою основної теореми інтегрального числення ми можемо знайти рішення аналітично. Оскільки модель проста, інтегральне числення видає пару вичерпних формул, які кажуть нам, скільки Ромео та Джульєта будуть кохати одні одного у будь-який момент часу в майбутньому. Представлені вище диференційні рівняння мають бути знайомі студентам фізикам: Ромео та Джульєта поводять себе як прості гармонічні осцилятори (маятники). Таким чином, модель передбачає, що функції R(t) і J(t), які описують зміни їх стосунків у часі, будуть синусоїдами, кожна з них зростаюча та спадаюча, але максимальні значення у них не збігаються. Модель можна зробити більш реалістичною різними шляхами. Наприклад, Ромео може реагувати не лише на почуття Джульєти, а й на свої власні. Раптом він один з тих хлопців, що настільки бояться, що їх кинуть, що почне охолоджувати свої почуття. Або відноситься до іншого типу хлопців, які обожнюють страждати – саме за це він її кохає. Додайте до цих сценаріїв ще два варіанти поведінки Ромео: він відповідає прив’язаністю Джульєти або посиленням, або послабленням власної прив’язаності – і побачите, що в романтичних стосунках існують чотири різні стилі поведінки. Мої студенти Пітер Кристофер з Вудстерського політехнічного інституту запропонували назвати представників таких типів так: Пустельник або Злісний Мізантроп для того Ромео, що охолоджує свої почуття й відсторонюється від Джульєти, і Нарцистичний Бовдур і Фліртуючий Фінк для того, який розігріває свій запал, проте відкидається Джульєтою (ви можете придумати свої назви для всіх цих типів). Хоча наведені приклади фантастичні, типи6 що їх описують, досить змістовні. Вони – найбільш потужні інструменти, які коли-небудь були створені людством для осмислення матеріального світу. Пан Ісаак Ньютон використовував диференціальні рівняння для відкриття таємниці руху планет. За допомогою цих рівнянь він об’єднав і небесні сфери, показавши, що і до тих і до інших використовуються однакові закони руху. Майже через 350 років після Ньютона людство прийшло до розуміння того, що закони фізики майже завжди можна виразити на мові диференційних рівнянь. Це істинно для рівнянь, що описують потоки тепла, повітря та води, для законів електрики та магнетизму, навіть для атому, де царює квантова механіка. У всіх випадках теоретична фізика повинна знайти правильні диференціальні рівняння та вирішити їх. Коли Ньютон знайшов ключ до таємниць Всесвіту і зрозумів його велику цінність, то вирішив опублікувати його у вигляді латинської анаграми. У вільному перекладі воно звучить так: «Корисно вирішувати диференціальні рівняння».(103) Безглузда ідея описати романтичні стосунки за допомогою диференціальних рівнянь прийшла до мене в голову, коли я був вперше закоханий і намагався зрозуміти поведінку моєї коханої дівчини. Це був літній роман наприкінці другого курсу коледжу. Я тоді дуже нагадував першого Ромео, а вона – першу Джульєту. Циклічність наших стосунків зводила мене з розуму, поки я не зрозумів, що ми обидва діяли за інерцією, у відповідності до простого правила «притягуй-відштовхуй». Проте до кінця літа моє рівняння почало розвалюватись, і я був ще більше спантеличений. Виявилось, що відбулась важлива подія, яке я не врахував: її колишній захотів її повернути. У математиці ми називаємо таку ситуацію задачею про трьох тіл. Вже наперед відомо, що вона нерозв’язна, особливо в контексті астрономії, де вперше і виникла. Після того як Ньютон вирішив диференціальні рівняння для задачі про два тіла (що пояснює, чому планети рухаються по еліптичним орбітам навколо Сонця), він звернув увагу на задачу про три тіла для Сонця, Землі та Місяця. Ні він, ні навколо інші вчені так і не змогли її вирішити. Пізніше з’ясували, що задача про три тіла містить насіння хаосу(104), тобто в довгостроковій перспективі їх поведінка непередбачувана. Ньютон нічого не знав про динаміку хаосу, але, за словами його друга Єдмунда Галлея(105), поскаржився, що задача трьох тіл «викликає в нього головний біль і так часто не дає йому спати, що він більше не буде про це думати». І тут ми з вами, пан Ісаак. У загальному випадку точного розв'язку за допомогою інтегралів не існує[1][2]. Проблема полягає в принциповій неможливості розв'язати диференційне рівняння 6-го порядку з нерозділеними змінними. Для окремих випадків знайдено точний розв'язок: Леонардом Ейлером (для колінеарного розташування точок) та Жозефом-Луї Лагранжем (для так званих трикутних точок Лагранжа). 1912 року фінський математик Карл Зундман знайшов аналітичний розв'язок загальної задачі у вигляді збіжного ряду[3]. Але цей розв'язок не є практичним, адже ряд збігається надзвичайно повільно (для застосування в астрономії необхідно обчислити більше 10^(8млн) членів ряду[4]).[1] Моделюванням задачі за допомогою чисельних методів знайдено деякі інші часткові розв'язки[5][6].