Презентація "Правильні многокутники"
Про матеріал
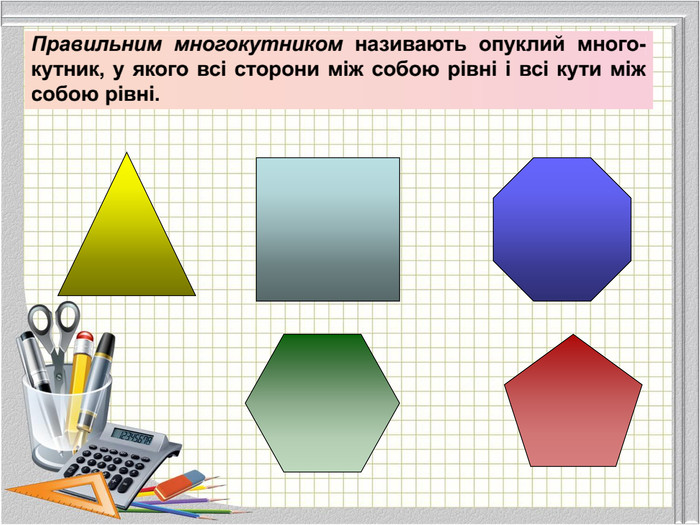
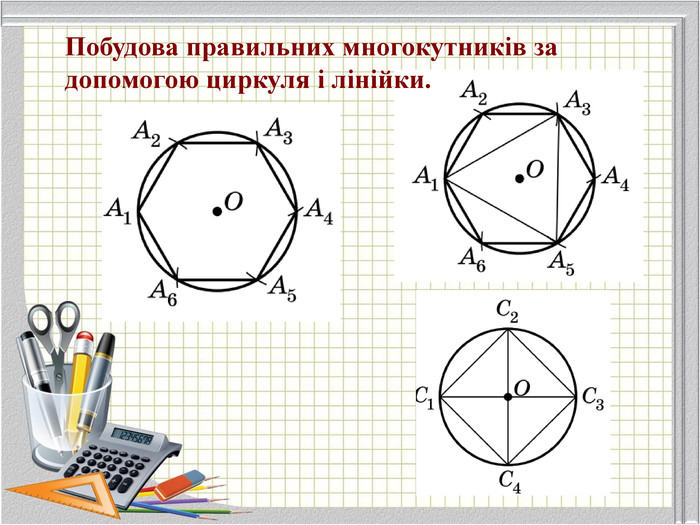
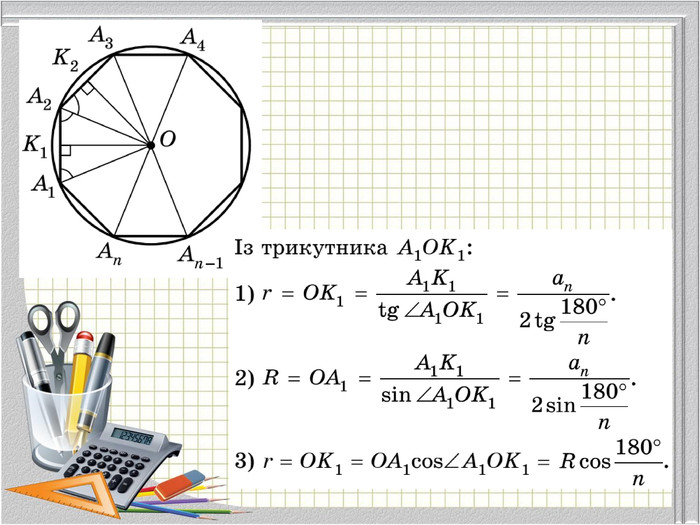
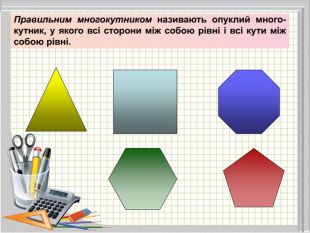
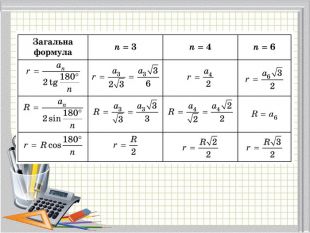
Матеріали презентації "Правильні многокутники" (п.15 "Геометрія 9 клас" ( О. С. Істер)) відповідає чинній програмі з математики.
Перегляд файлу
Зміст слайдів
ppt
До підручника
Геометрія 9 клас (Істер О. С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку