Презентация «Правильные многогранники»

Разработала: Полозенко Е.С.

Цель работы: ознакомить учащихся с видами правильных многогранников. Развить у них эстетическое восприятие математических фактов и расширить их кругозор. Способствовать познанию связи геометрии с природой. Сформировать представление о красоте связанной с симметрией.

Эпиграф: Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л. Кэрролл

ногогранник называется правильным, если он выпуклый, все его грани - равные правильные многоугольники, в каждой вершине сходится одинаковое число граней, все его двухгранные углы равны.

Существует пять видов правильных многогранников …

Правильный тетраэдр Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180є. Рис. 1

Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. Следовательно, сумма плоских углов при каждой вершине 240є. Правильный октаэдр Рис. 2

Правильный икосаэдр Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300є. Рис. 3

Составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270є. Куб (гексаэдр) Рис. 4

Правильный додекаэдр Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324є. Рис. 5

Названия многогранников пришли из Древней Греции, в них указывается число граней: «эдра»  грань; «тетра»  4; «гекса»  6; «окта»  8; «додека»  12. «икоса»  20;

Правильный многогранник Число граней вершин рёбер Тетраэдр 4 4 6 Куб 6 8 12 Октаэдр 8 6 12 Додекаэдр 12 20 30 Икосаэдр 20 12 30 Таблица № 1

Правильный многогранник Число граней и вершин (Г + В) рёбер (Р) Тетраэдр 4 + 4 = 8 6 Куб 6 + 8 = 14 12 Октаэдр 8 + 6 = 14 12 Додекаэдр 12 + 20 = 32 30 Икосаэдр 20 + 12 = 32 30 Таблица № 2

Сумма числа граней и вершин любого многогранника равна числу рёбер, увеличенному на 2. Г + В = Р + 2 Формула Эйлера Число граней плюс число вершин минус число рёбер в любом многограннике равно 2. Г + В  Р = 2

«Космический кубок» Кеплера Кеплер предположил, что существует связь между пятью правильными многогранниками и шестью открытыми к тому времени планетами Солнечной системы. Согласно этому предположению, в сферу орбиты Сатурна можно вписать куб, в который вписывается сфера орбиты Юпитера. В неё, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, к который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия. Такая модель Солнечной системы (рис. 6) получила название «Космического кубка» Кеплера. Результаты своих вычислений учёный опубликовал в книге «Тайна мироздания». Он считал, что тайна Вселенной раскрыта. Год за годом учёный уточнял свои наблюдения, перепроверял данные коллег, но, наконец, нашёл в себе силы отказаться от заманчивой гипотезы. Однако её следы просматриваются в третьем законе Кеплера, где говориться о кубах средних расстояний от Солнца. Модель Солнечной системы И. Кеплера Рис. 6

Идеи Платона и Кеплера о связи правильных многогранников с гармоничным устройством мира и в наше время нашли своё продолжение в интересной научной гипотезе, которую в начале 80-х гг. высказали московские инженеры В. Макаров и В. Морозов. Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обуславливают икосаэдро-додекаэдровую структуру Земли (рис. 7). Она проявляется в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки; 62 вершины и середины рёбер многогранников, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления. Здесь располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник. Дальнейшие исследования Земли, возможно, определят отношение к этой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место. Икосаэдро- додекаэдровая структура Земли Икосаэдро-додекаэдровая структура Земли Рис. 7

Правильные многогранники и природа Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр (рис. 8). Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи. Правильные многогранники – самые «выгодные» фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов. Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (NaCl) имеют форму куба (рис.9). При производстве алюминия пользуются алюминиево-калиевыми кварцами (K[Al(SO4)2]  12H2O), монокристалл которых имеет форму правильного октаэдра. Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра (рис.10). В разных химических реакциях применяется сурьменистый сернокислый натрий (Na5(SbO4(SO4)) – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра. Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора (В). В своё время бор использовался для создания полупроводников первого поколения. Рис. 8 Рис. 9 Рис. 10

Сальвадор Дали «Тайная вечеря» Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства. Бертран Рассел

Морис Эшер. “Рептилии”(литография, 1943 г).

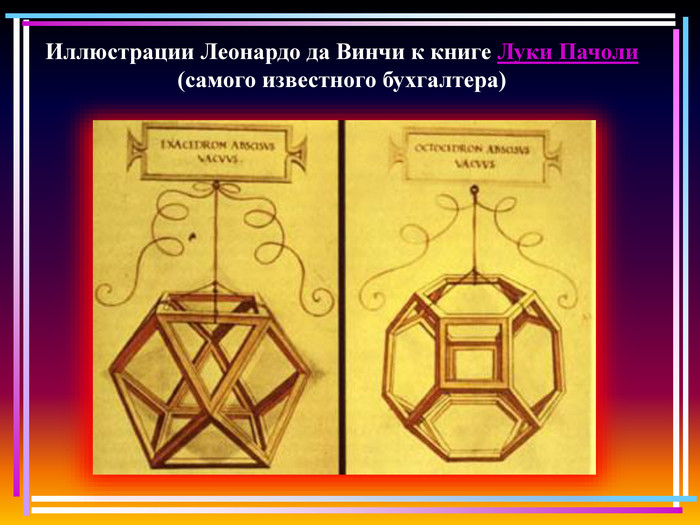
Надгробный памятник в кафедральном соборе Солсбери В знаменитом соборе в Солсбери столько интересных реликвий, что лишь немногие посетители бросят взгляд на надгробие Томаса Горджеса, усопшего в 1610 году. А между тем резьба на могильном камне содержит изображения додекаэдра, трёх икосаэдров и двух кубооктаэдров. На камне вырезаны скелетные каркасы этих тел в манере, близкой к использованной Леонардо да Винчи при построении моделей однородных многогранников с каркасом из прутьев.

Титульный лист книги Ж. Кузена «Книга о перспективе»

Иллюстрации Леонардо да Винчи к книге Луки Пачоли (самого известного бухгалтера)

Пришло время порешать!!!

Задача №1 1.Как разрезать запечатанный конверт и сложить из него тетраэдр? (На обеих сторонах конверта - у одного и того же края, начертить равносторонний треугольник и разрезать по пунктирной прямой. Правая его половина не нужна, а левую перегнуть по сторонам треугольника - на обеих сторонах конверта, и совместим точки А и В. Тетраэдр готов!)

2.Муха, разгуливая по 12 ребрам икосаэдра, проползает по каждому из них по крайней мере один раз. Каков наименьший путь, который должна проделать муха, чтобы побывать на всех ребрах икосаэдра?(Решению задачи может помочь проекция икосаэдра на плоскость ) Задача №2 (Кратчайшее расстояние, которое должна преодолеть муха для того, чтобы побывать на всех ребрах икосаэдра, равно 35 единицам (единица – длина ребра икосаэдра). Стерев пять ребер икосаэдра (например, ребра FM, BE, JA, ID и HC), мы получим граф, на котором нечетное число ребер сходится только в двух точках G и K. Поэтому муха может обойти весь этот граф (начав свой путь в точке G и закончив в точке K), пройдя по каждому ребру лишь один раз. Пройденное мухой расстояние равно 25 единицам. Если муха на своем пути встречает стертые ребра, мы просто добавляем их к пути из G в K, считая, что муха проходит их дважды. Пять стертых ребер, проходимых дважды,(10 единиц к уже пройденному пути). В сумме это составляет 35 единий.)

Домашнее задание: Сделать модель любого правильного многогранника. Можно использовать развёртки правильных многогранников: