Презентація "Просторові фігури. Початкові уявлення про многогранники"
Про матеріал
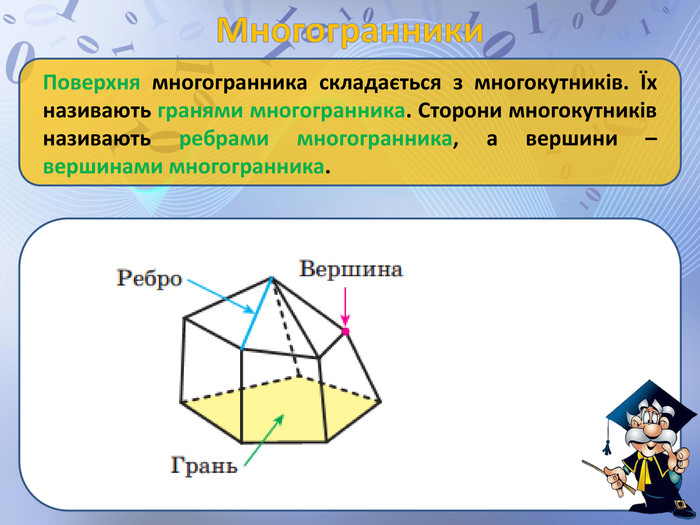
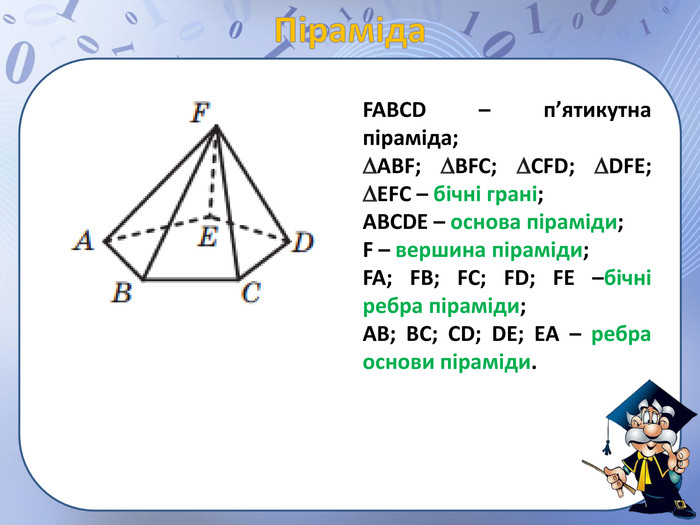
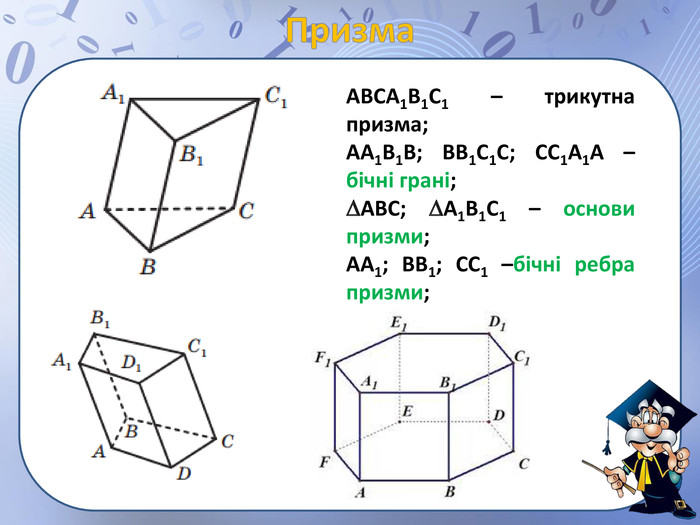
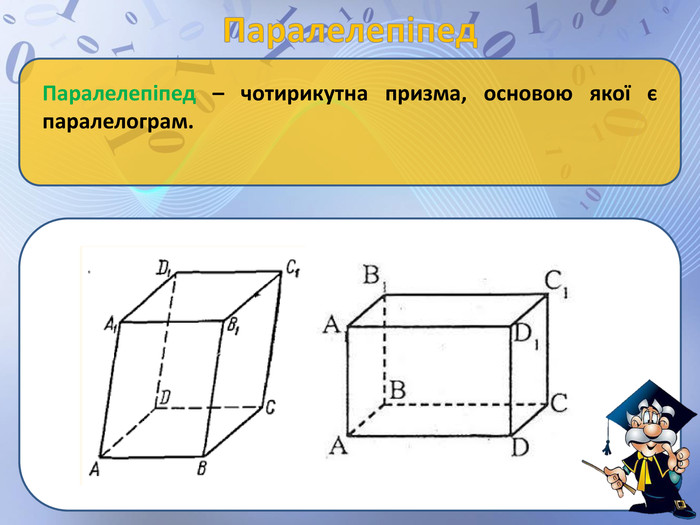
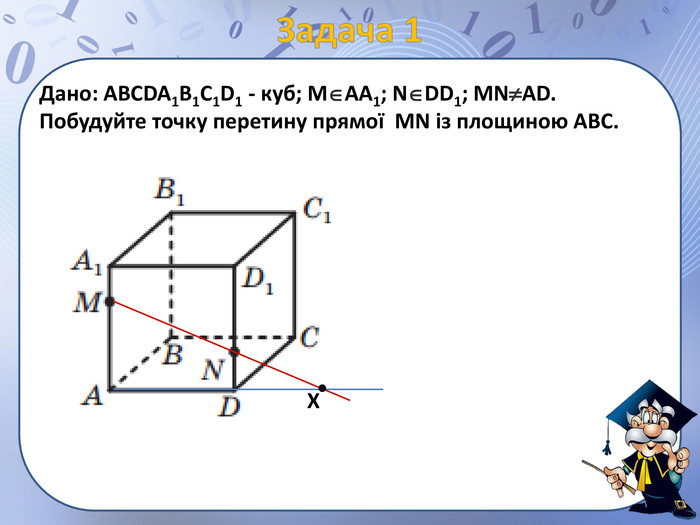
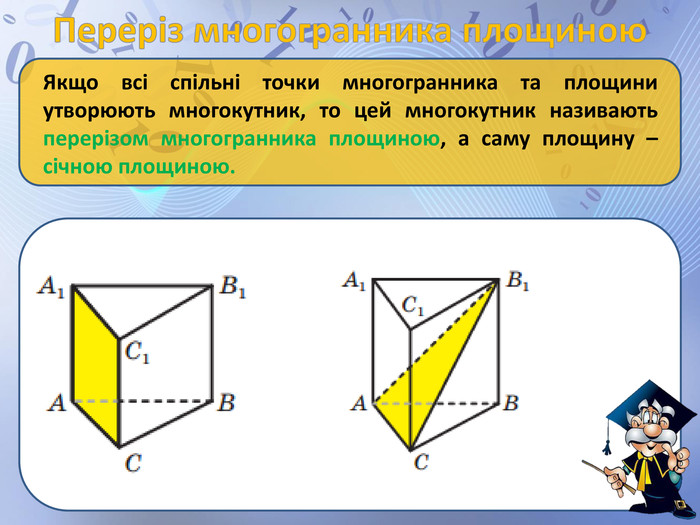
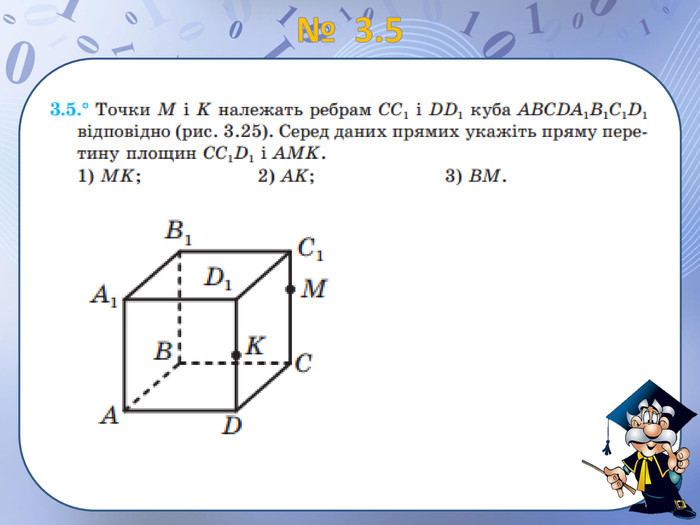
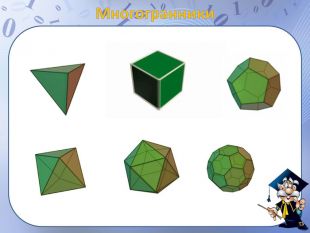
Презентація "просторові фігури. Початкові уявлення про многогранники" може бути використана для пояснення нового матеріалу по цій темі, містить анімовані побудови найпростіших перерізів, а також усні вправи. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку




















-

Гончаренко Галина Анатоліївна
20.11.2024 в 20:28
Дякую за можливість використати таку чудову презентацію!!! Матеріал та базові задачі відповідають змісту підручника. Ви - справжній професіонал, пані Людмило!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Бучман Марія
18.09.2024 в 07:06
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Єщенко Віра Іванівна
10.10.2023 в 08:41
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Константинова Олена Павлівна
21.09.2023 в 22:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Решетняк Марина Миколаївна
19.09.2023 в 00:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Хараб Євгенія Сергіївна
07.09.2023 в 20:24
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Матвій Галина
21.09.2022 в 22:07
Цікава розробка і продумане викладення матеріалу.
Дякую)
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ісаєва Тетяна
11.09.2022 в 20:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лаврентьева Лариса
12.09.2021 в 21:40
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 6 відгуків