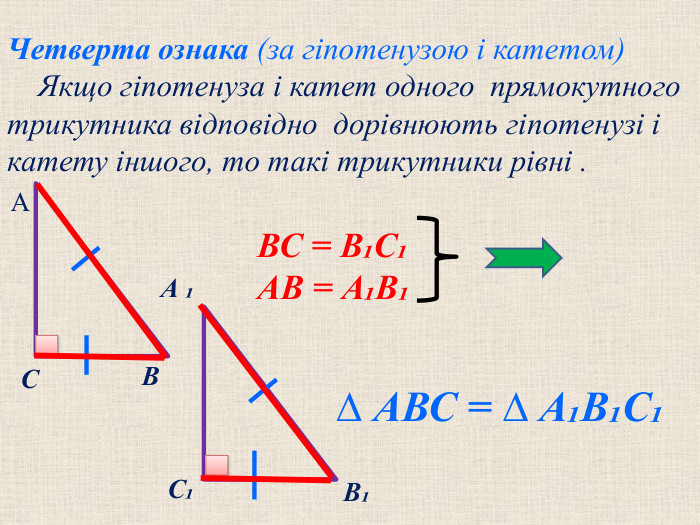
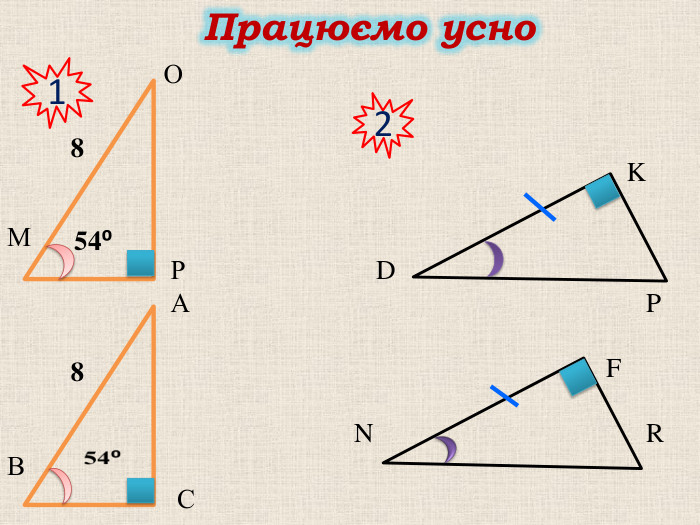
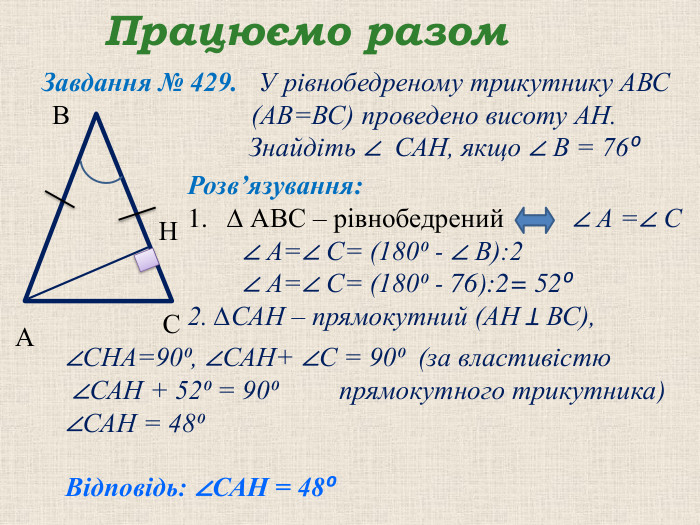
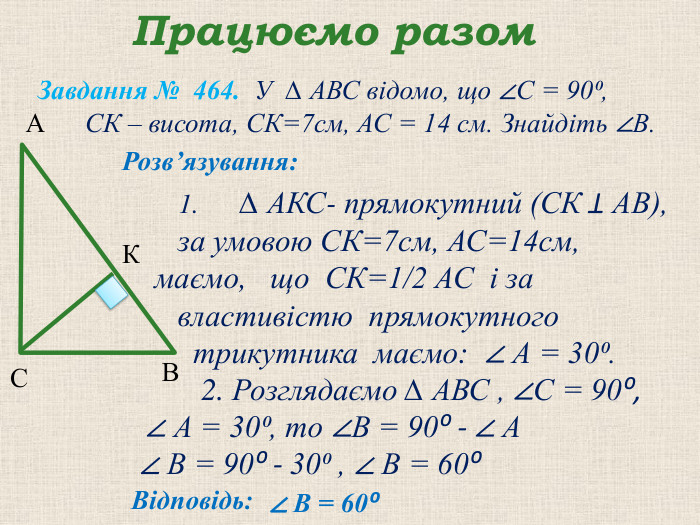
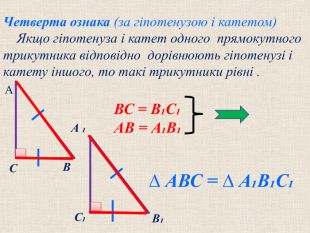
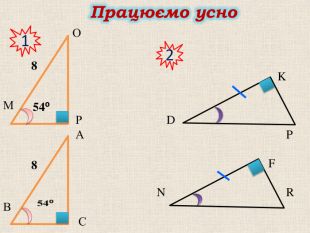
Презентація "Прямокутний трикутник"

Прямокутний трикутник. Властивості та ознакирівності прямокутних трикутників.7 клас. Вчитель математики. Криворучко Тетяна Вікторівна. Базаліївський ліцей

Девіз уроку

”У величезному саду геометрії кожний може підібрати собі букет за смаком” Давид Гільберт (німецький математик)

Скарбничка знань. Гра ”Вірю”/ Не вірю”У трикутнику є два кути тупі. У трикутнику є тупий і прямий кут. Сума гострих кутів прямокутного трикутник дорівнює 90⁰. Всі кути рівностороннього трикутника по 60⁰. Кути при основі рівнобедреного трикутника рівні. Сума кутів трикутника дорівнює 180⁰. У рівнобедреному трикутнику всі сторони рівні. У рівнобедреному трикутнику бічна сторона дорівнює основі. У трикутнику є два прямі кути. У рівнобедреного трикутника медіани всі рівні.

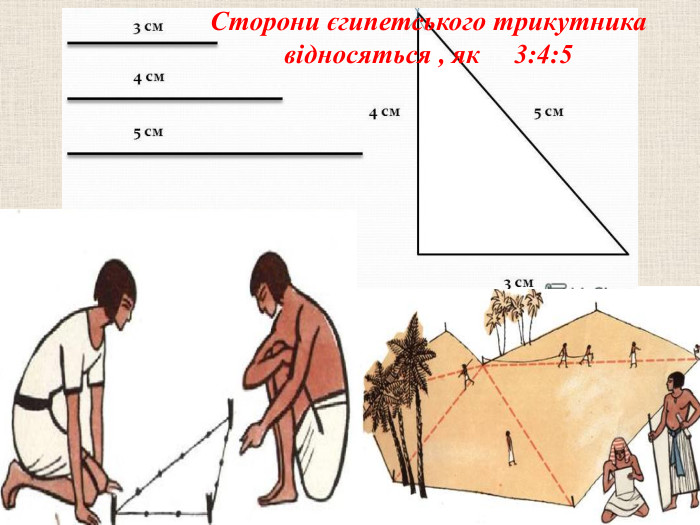
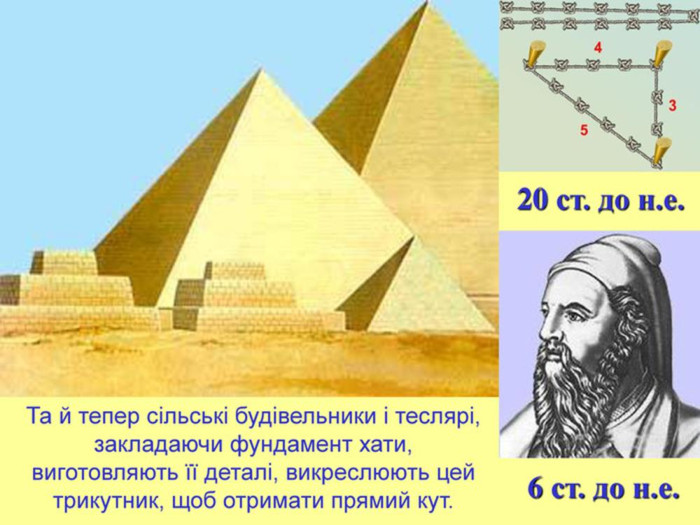
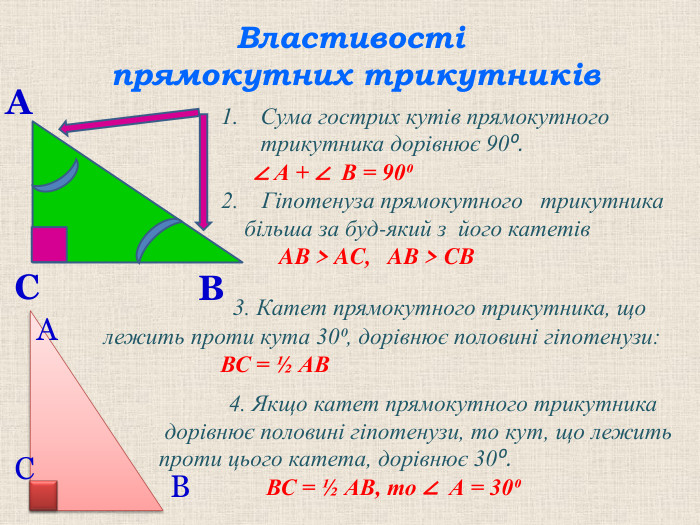
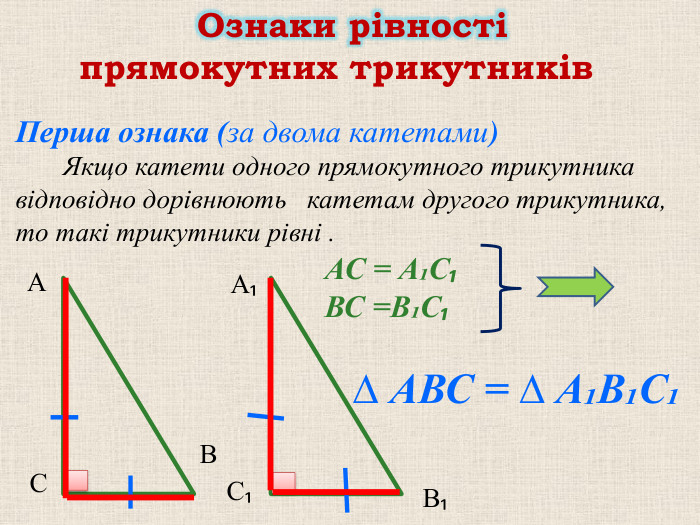
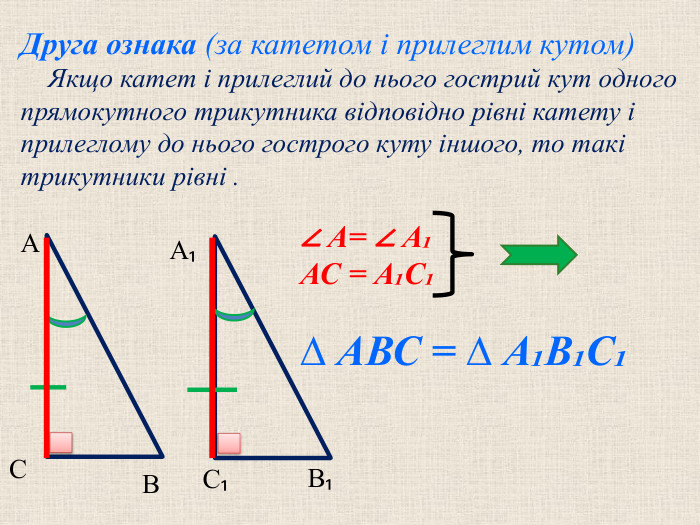
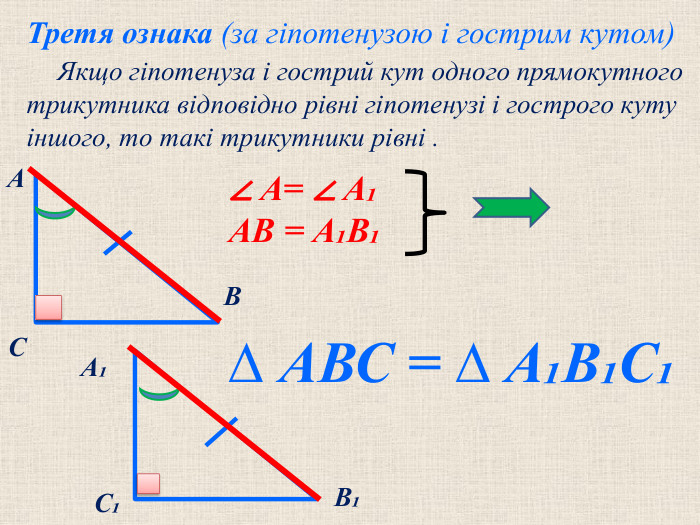
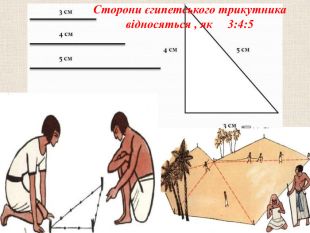
Історична довідка. Прямокутний трикутник – одна з перших геометричних фігур, про властивості якої людство знало ще в давнину. Задачі про трикутник знаходять у давньоєгипетських папірусах, стародавніх індійських книгах. Основні відомості про прямокутні трикутники були наведені Евклідом в його праці «Основи» (І книга) біля 300 років до н.р., згадка про трикутник часто зустрічаються в папірусі Ахмеса. Папірус Ахмеса

Сторони єгипетського трикутника відносяться , як 3:4:5

Означення: Прямокутний трикутник — трикутник, один із кутів якого прямий. style.colorfillcolorfill.type

Які з даних трикутників не є прямокутними аcnmebgdh

Прямокутний трикутник. Сторону прямокутного трикутника, протилежну прямому куту, називають гіпотенузою. Традиційно гіпотенузу позначають літерою с Сторони, які утворюють прямий кут (прилягають) називають катетами. Катети позначають літерами а і bаbс

Гіпотенуза – грецького походження: та, що тягнеться і стягує. Прообразом її є давньогрецька арфа, на якій струни стягували кінці двох взаємно перпендикулярних підставок. Катет – грецького походження, означає прямовисний, перпендикуляр

Властивості прямокутних трикутників. Сума гострих кутів прямокутного трикутника дорівнює 90⁰. ∠ А + ∠  В = 90⁰2. Гіпотенуза прямокутного трикутника більша за буд-який з його катетів AB > AC, AB > CB АCB A 3. Катет прямокутного трикутника, що лежить проти кута 30⁰, дорівнює половині гіпотенузи: ВС = ½ АВBC 4. Якщо катет прямокутного трикутника дорівнює половині гіпотенузи, то кут, що лежить проти цього катета, дорівнює 30⁰. ВС = ½ АВ, то ∠  А = 30⁰

Ознаки рівності прямокутних трикутників. Перша ознака (за двома катетами) Якщо катети одного прямокутного трикутника відповідно дорівнюють катетам другого трикутника, то такі трикутники рівні . А₁АС₁В₁ВСАС = А₁С₁ ВС =В₁С₁ ∆ АВС = ∆ А₁В₁С₁

Друга ознака (за катетом і прилеглим кутом) Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно рівні катету і прилеглому до нього гострого куту іншого, то такі трикутники рівні . ВАА₁СС₁В₁∠ А= ∠ А₁АС = А₁С₁∆ АВС = ∆ А₁В₁С₁

Третя ознака (за гіпотенузою і гострим кутом) Якщо гіпотенуза і гострий кут одного прямокутного трикутника відповідно рівні гіпотенузі і гострого куту іншого, то такі трикутники рівні .∠ А= ∠ А₁АВ = А₁В₁∆ АВС = ∆ А₁В₁С₁А₁АС₁В₁С В

Четверта ознака (за гіпотенузою і катетом) Якщо гіпотенуза і катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі і катету іншого, то такі трикутники рівні . ВС = В₁С₁АВ = А₁В₁ ∆ АВС = ∆ А₁В₁С₁ВВ₁А ₁АС₁С

Працюємо усно 8854⁰12 О KМ Р D А P F N RВ С

Працюємо разом. Завдання № 429. У рівнобедреному трикутнику АВС (АВ=ВС) проведено висоту АН. Знайдіть ∠  САН, якщо ∠ В = 76⁰ВАНСРозв’язування:∆ АВС – рівнобедрений ∠ А =∠ С ∠ А=∠ С= (180⁰ - ∠ В):2 ∠ А=∠ С= (180⁰ - 76):2= 52⁰2. ∆САН – прямокутний (АН Ʇ ВС), ∠СНА=90⁰, ∠САН+ ∠С = 90⁰ (за властивістю ∠САН + 52⁰ = 90⁰ прямокутного трикутника)∠САН = 48⁰Відповідь: ∠САН = 48⁰

Працюємо разом. Завдання № 464. У ∆ АВС відомо, що ∠С = 90⁰, СК – висота, СК=7см, АС = 14 см. Знайдіть ∠В. САВКРозв’язування: 1. ∆ АКС- прямокутний (СК Ʇ АВ), за умовою СК=7см, АС=14см, маємо, що СК=1/2 АС і за властивістю прямокутного трикутника маємо: ∠ А = 30⁰. 2. Розглядаємо ∆ АВС , ∠С = 90⁰, ∠ А = 30⁰, то ∠В = 90⁰ - ∠ А ∠ В = 90⁰ - 30⁰ , ∠ В = 60⁰ Відповідь: ∠ В = 60⁰

№1. Знайдіть кути прямокутного трикутника, якщо один із них дорівнює: а) 30°; б) 46°; в) 70°. №2. Знайдіть гострі кути прямокутного трикутника, якщо один із них більший за інший: а) удвічі; б) у 9 разів; в) на 30°. №3. Знайдіть кути рівнобедреного прямокутного трикутника. №4. Знайдіть менший з кутів, що утворює бісектриса прямого кута трикутника з гіпотенузою, якщо один з гострих кутів трикутника дорівнює 26°.

ПОТОЧНЕДля самостійної роботиhttps://wordwall.net/play/52380/533/864 wordwall

Підсумок уроку Математичний диктант. Закінчити речення: Трикутник, у якому є прямий кут, називають … прямокутним2. Сторону прямокутного трикутника, протилежну прямому куту називають … гіпотенузою3. Сторону прямокутного трикутника, прилеглу до прямого кута називають …катетом4. Сума гострих кутів прямокутного трикутника - …90⁰5. Довжина гіпотенузи прямокутного трикутника завжди … більша за довжину будь-якого катета.6. Катет прямокутного трикутника, що лежить проти кута …30⁰.., дорівнює половині гіпотенузи